Дискретная глобальная сетка
Эта документация требует внимания специалиста в области технологий . Конкретная проблема заключается в следующем: обзор английского языка и необходимость сокращения или обобщения некоторых частей. ( сентябрь 2018 г. ) |
| Геодезия |
|---|
 |
Дискретная глобальная сетка ( ДГГ ) — это мозаика , покрывающая всю поверхность Земли.Математически это разбиение пространства : оно состоит из набора непустых областей, образующих разбиение поверхности Земли. [1] В обычной стратегии моделирования сетки, чтобы упростить вычисления положения, каждый регион представлен точкой, абстрагируя сетку как набор точек региона. Каждая область или точка региона в сетке называется ячейкой .
Когда каждая ячейка сетки подвергается рекурсивному разделению, в результате чего образуется «серия дискретных глобальных сеток с постепенно увеличивающимся разрешением», [2] образуя иерархическую сетку, ее называют иерархической DGG (иногда «глобальная иерархическая мозаика»). [3] или «система DGG»).
Дискретные глобальные сетки используются в качестве геометрической основы для построения структур геопространственных данных . Каждая ячейка связана с объектами данных или значениями или (в иерархическом случае) может быть связана с другими ячейками. DGG были предложены для использования в широком спектре геопространственных приложений, включая векторное и растровое представление местоположения, объединение данных и пространственные базы данных. [1]
Наиболее распространенные сетки предназначены для представления горизонтального положения с использованием стандартной системы отсчета , такой как WGS84 . В этом контексте также принято использовать конкретный DGG в качестве основы для стандартизации геокодирования .
В контексте пространственного индекса DGG может назначать уникальные идентификаторы каждой ячейке сетки, используя их для целей пространственной индексации, в базах геоданных или для геокодирования .
Эталонная модель земного шара
[ редактировать ]«Глобус» в концепции DGG не имеет строгой семантики, но в геодезии так называемая « система координат сетки » представляет собой сетку, которая делит пространство с точными положениями относительно исходной точки , то есть является аппроксимированной «стандартной моделью Геоид » . Итак, в роли геоида «глобусом», охватываемым ДГГ, может быть любой из следующих объектов:
- Топографическая поверхность Земли , когда каждая ячейка сетки имеет свои координаты положения на поверхности и высоту относительно стандартного геоида . Пример: сетка с координатами ( φ , λ , z ), где z — высота.
- Стандартная . геоида поверхность Координата z равна нулю для всей сетки, поэтому ее можно опустить ( φ , λ ).
Древние стандарты, существовавшие до 1687 года (публикация «Начал» Ньютона), использовали «сферу отсчета»; в настоящее время геоид математически абстрагируется как опорный эллипсоид .- : Упрощенный геоид иногда необходимо принять старый геодезический стандарт (например, SAD69 ) или негеодезическую поверхность (например, идеально сферическую поверхность), которая будет покрыта сеткой. В этом случае ячейки должны быть помечены однозначным образом (φ',λ') преобразование ( φ , λ ) ⟾ ( φ ′ , λ ′ ). и должно быть известно
- Проекционная поверхность . Обычно географические координаты ( φ , λ ) проецируются ( с некоторыми искажениями ) на плоскость двумерного отображения с двумерными декартовыми координатами ( x , y ).
В качестве глобального процесса моделирования современные DGG, включая процесс проецирования, имеют тенденцию избегать таких поверхностей, как цилиндр или конические тела, что приводит к разрывам и проблемам с индексацией. Правильные многогранники и другие топологические эквиваленты сферы привели к появлению наиболее многообещающих известных вариантов, которые могут быть охвачены DGG: [1] потому что «сферические проекции сохраняют правильную топологию Земли - нет никаких особенностей или разрывов, с которыми нужно было бы иметь дело». [4]
При работе с DGG важно указать, какой из этих вариантов был принят. Итак, характеристику эталонной модели шара ДГГ можно резюмировать следующим образом:
- Восстановленный объект : тип объекта в роли глобуса. Если проекции нет, объектом, покрываемым сеткой, является геоид, Земля или сфера; else — геометрический класс поверхности проекции (например, цилиндр, куб или конус).
- Тип проекции : отсутствует (нет проекции) или имеется. Если она присутствует, ее характеристика может быть суммирована с помощью целевого свойства проекции (например, равновеликая, конформная и т. д.) и класса корректирующей функции (например, тригонометрической, линейной, квадратичной и т. д.).
ПРИМЕЧАНИЕ. Когда DGG покрывает поверхность проекции, в контексте происхождения данных также важны метаданные об эталонном геоиде — обычно они сообщают значение CRS по ISO 19111 , без путаницы с поверхностью проекции.
Типы
[ редактировать ]Основной отличительной особенностью классификации или сравнения DGG является использование или отсутствие иерархических сеточных структур:
- В иерархических системах ссылок каждая ячейка представляет собой «блочную ссылку» на подмножество ячеек, и идентификаторы ячеек могут выражать эту иерархию в ее логике или структуре нумерации.
- В неиерархических системах отсчета каждая ячейка имеет отдельный идентификатор и представляет собой область пространства фиксированного масштаба. Дискретизация системы широты/долготы является наиболее популярной и стандартной для преобразований.
Другими обычными критериями классификации DGG являются форма плитки и степень детализации ( разрешение сетки ):
- Правильность и форма плитки : бывает правильная, полуправильная или неправильная сетка . Как и в случае с обычными мозаиками из правильных многоугольников , можно использовать мозаику с правильной гранью (например, настенная плитка может быть прямоугольной, треугольной, шестиугольной и т. д.) или с тем же типом грани, но с изменением ее размера или углов, что приводит к получению полуправильных форм.
Единообразие формы и регулярность метрик обеспечивают лучшие алгоритмы индексации сетки. Хотя практическое применение у него меньше, возможны совершенно нерегулярные сетки, например, в покрытии Вороного . - Мелкая или грубая грануляция (размер ячейки): современные DGG можно параметризовать по разрешению сетки, поэтому это характеристика окончательного экземпляра DGG, но бесполезная для классификации DGG, за исключением случаев, когда тип DGG должен использовать определенное разрешение или иметь предел дискретизации. «Мелкая» сетка грануляции не имеет ограничений, а «грубая» означает резкое ограничение. Исторически основные ограничения связаны с цифровыми/аналоговыми носителями, сжатием/расширением представления сетки в базе данных и ограничениями памяти для хранения сетки. Когда необходима количественная характеристика, можно принять среднюю площадь ячеек сетки или среднее расстояние между центрами ячеек.
Примеры
[ редактировать ]Неиерархические сетки
[ редактировать ]Наиболее распространенным классом дискретных глобальных сеток являются те, в которых центральные точки ячеек размещаются на меридианах долготы/широты и параллелях или которые используют меридианы и параллели долготы/широты для формирования границ прямоугольных ячеек. Примеры таких сеток, основанных на широте/долготе:
| UTM-зоны : Делит Землю на шестьдесят (полосных) зон, каждая из которых представляет собой полосу долготы в шесть градусов. В цифровых носителях убирается зона перекрытия. Используйте секущую поперечную проекцию Меркатора в каждой зоне. Определите 60 секущих цилиндров, по 1 на зону. Зоны UTM были расширены с помощью системы Military Grid Reference System (MGRS) за счет добавления полос широты . |  | |||
| начало: 1940-е годы | накрытый объект: цилиндр (60 вариантов) | проекция: UTM или широта | плитка неправильной формы: многоугольные полосы | зернистость: грубая |
| (современный) UTM – Универсальный поперечный Меркатор : Представляет собой дискретизацию непрерывной сетки UTM со своего рода двухуровневой иерархией, где первый уровень (крупное зерно) соответствует «зонам UTM с полосами широт» ( MGRS ), использует те же 60 цилиндров в качестве опорной проекции. объекты. Каждая мелкозернистая ячейка обозначается структурированным идентификатором, состоящим из «обозначения зоны сетки», «квадратного идентификатора площадью 100 000 метров» и «числового местоположения». Разрешение сетки является прямой функцией количества цифр в координатах, что также стандартизируется. Например, ячейка 17N 630084 4833438 представляет собой квадрат размером примерно 10х10 м. PS: в этом стандарте для проекций используется 60 отдельных цилиндров. Существуют также стандарты «Регионального поперечного Меркатора» (RTM или UTM Regional) и «Локального поперечного Меркатора» (LTM или UTM Local) с более конкретными цилиндрами для лучшего соответствия и точности в интересующей точке. |  | |||
| начало: 1950-е годы | накрытый объект: цилиндр (60 вариантов) | проекция: UTM | прямоугольная плитка: равноугольная (конформная) | детализация: мелкая |
| ИСО 6709 : Дискретизирует традиционное представление в виде координатной сетки и современные местоположения на основе ячеек с числовыми координатами. Степень детализации фиксируется с помощью простого соглашения о числовом представлении, например, сетка в один градус, сетка с шагом 0,01 градус и т. д., что приводит к образованию ячеек с неравной площадью в сетке. Форма ячеек прямоугольная, за исключением полюсов, где они треугольные. Числовое представление стандартизировано двумя основными соглашениями: градусами (Приложение D) и десятичными числами (Приложение F). Разрешение сетки определяется количеством цифр (Приложение H). | 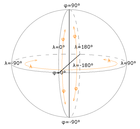 | |||
| начало: 1983 г. | покрытый объект: геоид (любой CRS ISO 19111 ) | проекция: нет | прямоугольная плитка: равномерная сфероидальная форма | детализация: мелкая |
| Первичная марка ( TIN DEM ): Векторная треугольная нерегулярная сеть (TIN) — набор данных TIN DEM также называется первичной (измеренной) DEM. Многие матрицы высот создаются на основе сетки точек, расположенных с регулярным угловым шагом по широте и долготе. Примеры включают Глобальный набор данных о высотах за 30 угловых секунд (GTOPO30) . [5] и Глобальные данные о высоте местности в разных разрешениях за 2010 год (GMTED2010). [6] Треугольная нерегулярная сеть представляет собой представление непрерывной поверхности, состоящей полностью из треугольных граней. |  | |||
| начало: 1970-е годы | накрытый объект: местность | проекция: нет | треугольные неоднородные плитки: параметризованные (векторные) | детализация: мелкая |
| Сетки Аракавы : Используется для моделей системы Земли для метеорологии и океанографии — например, Глобальная многомасштабная модель окружающей среды (GEM) использует сетки Аракавы для моделирования глобального климата . [7] Эталонный DGG под названием «A-grid» для сравнения с другими DGG. Использовался в 1980-х годах с пространственным разрешением ~ 500x500. | ||||
| начало: 1977 г. | накрытый объект: геоид | проекция: ? | прямоугольные плитки: параметрические, пространство-время | зернистость: средняя |
| Квадраты ВМО : Специализированная сетка, используемая исключительно NOAA, делит карту мира с линиями сетки по широте и долготе на ячейки сетки размером 10 ° широты и 10 ° долготы, каждая из которых имеет уникальный четырехзначный цифровой идентификатор (первая цифра идентифицирует квадранты NE/NE). ЮВ/ЮЗ/СЗ). | ||||
| начало: 2001 г. | накрытый объект: геоид | проекция: нет | Обычные плитки: прямоугольные ячейки 36х18. | зернистость: грубая |
| Квадраты мировой сетки: Являются совместимым расширением японских квадратов сетки, стандартизированных в промышленных стандартах Японии (JIS X0410), для использования во всем мире. Код World Grid Square может идентифицировать квадраты сетки, покрывающие мир, на основе девяти слоев. Мы можем выразить квадрат сетки, используя последовательность от 6 до 16 цифр в зависимости от ее разрешения. [8] | ||||
| начало: 2015 г. | накрытый объект: геоид | проекция: нет | Обычные плитки: прямоугольные ячейки | зернистость: крупная, средняя, мелкая |
Иерархические сетки
[ редактировать ]
На иллюстрации справа показаны три карты границ побережья Великобритании. Первая карта была покрыта сеткой уровня 0 с ячейками размером 150 км. Только серая ячейка в центре, без необходимости масштабирования для детализации, остается уровнем 0; все остальные ячейки второй карты были разделены на сетку из четырех ячеек (уровень сетки-1), каждая по 75 км. На третьей карте 12 ячеек уровня 1 остались серыми, все остальные были снова разделены, каждая ячейка уровня 1 преобразована в сетку уровня 2.
Примеры DGG , которые используют такой рекурсивный процесс создания иерархических сеток, включают:
| Дискретные глобальные сети ISEA (ISEA DGG): — это класс сеток, предложенный исследователями из Университета штата Орегон . [1] Ячейки сетки создаются в виде правильных многоугольников на поверхности икосаэдра , а затем обратно проецируются с использованием икосаэдральной картографической проекции Снайдера (ISEA). [9] образовать на сфере ячейки равной площади. Ориентация икосаэдра относительно Земли может быть оптимизирована по разным критериям. [10] Ячейки могут представлять собой шестиугольники, треугольники или четырехугольники . Множественные разрешения обозначаются выбором апертуры или соотношения площадей ячеек при последовательных разрешениях. Некоторые приложения ISEA DGG включают продукты данных, генерируемые спутником Европейского космического агентства для измерения влажности почвы и солености океана (SMOS), который использует ISEA4H9 (апертура 4, шестиугольное разрешение DGGS 9), [11] и коммерческое программное обеспечение Global Grid Systems Insight, [12] в котором используется ISEA3H (диафрагма 3, шестиугольный DGGS). | ||||
| Год создания: 1992..2004 г. | крытый объект: ? | проекция: равновеликая | параметризованные (шестиугольники, треугольники или четырехугольники) плитки: равновеликие | детализация: мелкая |
| COBE – четырехсторонний сферический куб : Куб: [13] Декомпозиция сферы аналогична HEALPix и S2. Но не используется кривая, заполняющая пространство, края не являются геодезическими, а проекция более сложна. | ||||
| Год создания: 1975..1991 | закрытый объект: куб | проекция: криволинейная перспектива | четырехугольная плитка: равномерная, сохраняющая площадь | детализация: мелкая |
| Четвертичная треугольная сетка (QTM): QTM имеет ячейки треугольной формы, созданные в результате 4-кратного рекурсивного деления сферического октаэдра. [14] [15] | ||||
| Год создания: 1999...2005 гг. | накрытый объект: октаэдр (или другой) | проекция: равновеликий цилиндр Ламберта. | треугольные плитки: равномерная площадь с сохранением площади | детализация: мелкая |
| Иерархическая равновеликая пикселизация isoLatitude ( HEALPix ): HEALPix имеет ячейки четырехугольной формы одинаковой площади и изначально был разработан для использования с наборами астрофизических данных всего неба. [16] Обычная проекция — «H?4, K?3 HEALPix».Основное преимущество по сравнению с другими продуктами той же ниши индексации, что и S2, «подходит для расчетов с участием сферических гармоник». [17] |  | |||
| начало: 2006 г. | крытый объект: Геоид | проекция: (K,H) параметризованная проекция HEALPix | четырехугольные плитки: равномерная с сохранением площади | детализация: мелкая |
| Иерархическая треугольная сетка (HTM): Разработанный в 2003...2007 годах, HTM «представляет собой многоуровневое рекурсивное разложение сферы. Оно начинается с октаэдра, пусть это будет уровень 0. Когда вы проецируете края октаэдра на (единичную) сферу, создается 8 сферических треугольников: 4 в северном и 4 в южном полушариях». [18] Затем каждый треугольник разбивается на 4 подтреугольника (разбиение 1 на 4). Кажется, первая публичная действующая версия [19] HTM-v2 в 2004 году. |  | |||
| начало: 2004 г. | крытый объект: Геоид | проекция: нет | треугольные плитки: сферические эквалатеры | детализация: мелкая |
| Геохэш : Широта и долгота объединяются, соединяя биты в объединенном числе. Двоичный результат представлен в формате base32, что обеспечивает компактный, удобочитаемый код. При использовании в качестве пространственного индекса соответствует кривой Z-порядка . Есть несколько вариантов, таких как Geohash-36 . |  | |||
| начало: 2008 г. | крытый объект: Геоид | проекция: нет | полуправильная плитка: прямоугольная | детализация: мелкая |
| S2/S2Регион: «Система сеток S2» является частью «Библиотеки геометрии S2». [20] (название происходит от математического обозначения n сферы - S н ). Он реализует систему индексов, основанную на кубической проекции и заполняющей пространство кривой Гильберта , разработанной в Google . [21] [22] S2Region для S2 является наиболее общим представлением его ячеек, где можно рассчитать положение ячейки и метрику (например, площадь). Каждый S2Region представляет собой подсетку, в результате чего иерархия ограничена 31 уровнем. На уровне 30 разрешение оценивается [23] в 1 см 2 , на уровне 0 составляет 85011012 км. 2 . Идентификатор ячейки иерархической сетки грани куба (6 граней) имеет идентификатор 60 бит (так что «каждый см 2 на Земле можно представить с помощью 64-битного целого числа). |  | |||
| начало: 2015 г. | закрытый объект: куб | проекция: сферические проекции на каждой грани куба с использованием квадратичной функции. | полуправильные плитки: четырехсторонние проекции | детализация: мелкая |
| S2/S2LatLng: DGG предоставляется представлением S2LatLng, подобным сетке ISO 6709, но иерархической и со своей специфической формой ячеек. | ||||
| начало: 2015 г. | накрытый объект: геоид или сфера | проекция: нет | полуправильная плитка: четырехугольная | детализация: мелкая |
| S2/S2CellId: DGG предоставляется представлением S2CellId. Каждый идентификатор ячейки представляет собой 64-битный уникальный целочисленный идентификатор без знака для любого уровня иерархии. | ||||
| начало: 2015 г. | закрытый объект: куб | проекция: ? | полуправильная плитка: четырехугольная | детализация: мелкая |
Стандартные равновеликие иерархические сетки
[ редактировать ]Существует класс иерархических DGG, названный Открытым геопространственным консорциумом (OGC) «дискретными глобальными сеточными системами» ( DGGS ), которые должны удовлетворять 18 требованиям. Среди них, что лучше всего отличает этот класс от других иерархических DGG, это Требование-8: «Для каждого последующего уровня детализации сетки и для каждой геометрии ячеек (...) Ячейки одинаковой площади (...) внутри заданный уровень точности» . [24]
DGGS спроектирована как информационная основа в отличие от обычных систем координат, изначально разработанных для навигации. Чтобы глобальная пространственная информационная система на основе сетки могла эффективно работать в качестве аналитической системы, она должна быть построена с использованием ячеек, которые однородно представляют поверхность Земли. [24] Стандарт DGGS включает в свои требования набор функций и операций, которые должна предлагать платформа.
Все ячейки DGGS уровня 0 представляют собой равные по площади грани правильных многогранников ...

Структура DGGS
[ редактировать ]Стандарт определяет требования к иерархической DGG , в том числе способы управления сетью. Любой DGG, удовлетворяющий этим требованиям, может называться DGGS. «Спецификация DGGS ДОЛЖНА включать в себя опорный кадр DGGS и связанные с ним функциональные алгоритмы, как определено базовой концептуальной моделью данных DGGS» . [25]
- Чтобы система сетки Земли соответствовала настоящей Абстрактной спецификации, она должна определять иерархическую мозаику ячеек равной площади, которые одновременно разделяют всю Землю на нескольких уровнях детализации и обеспечивают глобальную пространственную систему отсчета. Система также должна включать методы кодирования для: адресации каждой ячейки; назначать квантованные данные ячейкам; и выполнять алгебраические операции над ячейками и присвоенными им данными. Основные понятия базовой концептуальной модели данных DGGS:
- элементы системы отсчета и,
- элементы функционального алгоритма; включающий:
- операции квантования,
- алгебраические операции и
- операции интероперабельности.
Моделирование базы данных
[ редактировать ]
Существует много DGG, потому что существует множество альтернатив представления, оптимизации и моделирования. Вся сетка DGG представляет собой композицию своих ячеек, и в иерархическом DGG каждая ячейка использует новую сетку в своей локальной области.
Иллюстрация не подходит для случаев TIN DEM и подобных структур «необработанных данных», где база данных использует не концепцию ячейки (которая геометрически представляет собой треугольную область), а узлы и края: каждый узел представляет собой высоту, а каждое ребро — это расстояние. между двумя узлами.
В общем, каждая ячейка DGG идентифицируется координатами ее точки региона (показанной как центральная точка представления базы данных). Также возможно, с потерей функциональности, использовать «свободный идентификатор», то есть любой уникальный номер или уникальную символическую метку для каждой ячейки, идентификатор ячейки . Идентификатор обычно используется в качестве пространственного индекса (например, внутреннего квадродерева или дерева kd ), но его также можно преобразовать в удобочитаемую метку для приложений геокодирования .
Современные базы данных (например, с использованием сетки S2) также используют несколько представлений для одних и тех же данных, предлагая как сетку (или область ячеек), основанную на геоиде, так и сетку в проекции.
История
[ редактировать ]Дискретные глобальные сетки с областями ячеек, определяемыми параллелями и меридианами широты и долготы, использовались с самых первых дней глобальных геопространственных вычислений . До этого дискретизация непрерывных координат для практических целей с помощью бумажных карт происходила только с низкой степенью детализации. Пожалуй, наиболее репрезентативным и главным примером DGG этой доцифровой эпохи были военные UTM DGG 1940-х годов с более тонкой гранулированной идентификацией ячеек для целей геокодирования . Точно так же некоторая иерархическая сетка существует до геопространственных вычислений, но только в грубой детализации.
Глобальная поверхность не требуется для использования на ежедневных географических картах, а до 2000-х годов память была очень дорогой, чтобы поместить все планетарные данные в один и тот же компьютер. Первые цифровые глобальные сетки использовались для обработки данных спутниковых изображений и моделирования глобальной ( климатической и океанографической ) гидродинамики.
Первые опубликованные ссылки на иерархические геодезические системы DGG относятся к системам, разработанным для моделирования атмосферы и опубликованным в 1968 году. Эти системы имеют области шестиугольных ячеек, созданные на поверхности сферического икосаэдра . [26] [27]
Пространственные иерархические сетки стали объектом более интенсивных исследований в 1980-х годах. [28] когда основные структуры, такие как Quadtree , были адаптированы для индексации изображений и баз данных.
Хотя отдельные экземпляры этих сеток использовались десятилетиями, термин «дискретные глобальные сетки» был придуман исследователями из Университета штата Орегон в 1997 году. [2] для описания класса всех таких сущностей.
... Стандартизация OGC в 2017 году...
Сравнение и эволюция
[ редактировать ]
Оценочная дискретная глобальная сетка состоит из многих аспектов, включая площадь, форму, компактность и т. д.Методы оценки картографической проекции , такие как индикатриса Тиссо , также подходят для оценки дискретной глобальной сетки на основе картографической проекции.
Кроме того, усредненное соотношение между взаимодополняющими профилями (AveRaComp) [29] дает хорошую оценку искажений формы дискретной глобальной сетки четырехугольной формы.
Выбор и адаптация при разработке баз данных ориентированы на практические требования к большей производительности, надежности и точности. Лучшие варианты отбираются и адаптируются к потребностям, способствуя развитию архитектур DGG. Примеры этого процесса эволюции: от неиерархических к иерархическим DGG; от использования индексов Z-кривой ( простой алгоритм, основанный на переплетении цифр), используемых Geohash, до индексов Гильбертовой кривой, используемых в современных оптимизациях, таких как S2.
Варианты геокодирования
[ редактировать ]В общем случае каждая ячейка сетки идентифицируется координатами ее точки региона, но также можно упростить синтаксис и семантику координат, получить идентификатор, как в классических буквенно-цифровых сетках — и найти координаты региона. -точка от его идентификатора. Маленькое и быстрое представление координат является целью реализации Cell-ID для любых решений DGG.
, функциональность не теряется При использовании «свободного идентификатора» вместо координаты, то есть любого уникального числа (или уникальной символической метки) для каждой точки региона, идентификатора ячейки . Таким образом, преобразование координаты в удобочитаемую метку и/или сжатие длины метки является дополнительным шагом в представлении сетки. Это представление называется геокодом .
Некоторые популярные « глобальные географические коды », такие как ISO 3166-1 альфа-2 для административных регионов или код Лонгхерста для экологических регионов земного шара, частично охватывают земной шар. С другой стороны, любой набор идентификаторов ячеек конкретного DGG может использоваться как « коды места с полным покрытием ». Каждый отдельный набор идентификаторов, используемый в качестве стандарта для целей обмена данными, называется «системой геокодирования».
Существует множество способов представления значения идентификатора ячейки ( cell-ID ) сетки: структурированный или монолитный, двоичный или нет, читаемый человеком или нет. Предположим, что объект карты, такой как сингапурский фонтан Мерлион (объект масштаба ~ 5 м), представлен минимальной ограничивающей ячейкой или ячейкой центральной точки, идентификатор ячейки будет:
| Идентификатор ячейки | Название и параметры варианта DGG | структура идентификатора; разрешение сетки |
|---|---|---|
| (1° 17 ′ 13,28″ с.ш., 103° 51 ′ 16,88″ в.д.) | ISO 6709/D в градусах (Приложение), CRS = WGS84. | годы ( deg min sec dir) длинный ( deg min sec dir); секунды с двумя дробными знаками |
| (1.286795, 103.854511) | ISO 6709/F в десятичном формате и CRS = WGS84. | (lat,long); 6 дробных мест |
| (1.65AJ, 2В.IBCF) | ISO 6709/F в десятичном формате Base36 (не ISO) и CRS = WGS84. | (lat,long); 4 дробных места |
| w21z76281 | Геохеш, base32, WGS84 | монолитный; 9 персонажей |
| 6ПХ57ВП3+ПР | ПлюсКод, base20, WGS84 | монолитный; 10 персонажей |
| 48Н 372579 142283 | UTM, стандартное десятичное число, WGS84 | zone lat long; 3 + 6 + 6 цифр |
| 48Н 7ЖФ 31СБ | UTM, координаты base36, WGS84 | zone lat long; 3 + 4 + 4 цифры |
Все эти геокоды представляют одно и то же положение на земном шаре с одинаковой точностью, но различаются длиной строки , использованием разделителей и алфавитом (символами, не являющимися разделителями). В некоторых случаях можно использовать «исходное представление DGG». Варианты представляют собой незначительные изменения, затрагивающие только окончательное представление, например, основу числового представления или переплетение частей структурированного только в одно числовое или кодовое представление. Наиболее популярные варианты используются для приложений геокодирования.
Буквенно-цифровые глобальные сетки
[ редактировать ]DGG и его варианты с удобочитаемыми идентификаторами ячеек использовались в качестве фактического стандарта для буквенно-цифровых сеток . Он не ограничивается буквенно-цифровыми символами, но «буквенно-цифровой» является наиболее распространенным термином.
Геокоды — это обозначения местоположений, а в контексте DGG — обозначения для обозначения идентификаторов ячеек сетки. Цифровые стандарты и DGG постоянно развиваются, поэтому в последние годы популярность каждого соглашения о геокодировании постоянно меняется. Более широкое внедрение также зависит от принятия правительством страны, использования на популярных картографических платформах и многих других факторов.
Примеры, использованные в следующем списке, относятся к «малой ячейке сетки», содержащей обелиск Вашингтона . 38° 53′ 22.11″ N, 77° 2′ 6.88″ W.
| Имя DGG/вар | Создание и лицензия | Краткое описание варианта | Описание и пример |
|---|---|---|---|
| UTM-зоны/непересекающиеся | 1940-е годы - CC0 | оригинал без дублирования | Делит Землю на шестьдесят многоугольных полос. Пример: 18S |
| Дискретный UTM | 1940-е годы - CC0 | исходные целые числа UTM | Делит Землю на шестьдесят зон, каждая из которых представляет собой полосу долготы в шесть градусов, и использует секущую поперечную проекцию Меркатора в каждой зоне. Нет информации о первом цифровом использовании и соглашениях. Предполагалось, что стандартизации были позже ISO (1980-е годы). Пример: 18S 323483 4306480 |
| ИСО 6709 | 1983 | оригинальное представление степени | Разрешение сетки является функцией количества цифр — при необходимости заполняются ведущие нули, а дробная часть содержит соответствующее количество цифр для представления требуемой точности сетки. Пример: 38° 53′ 22.11″ N, 77° 2′ 6.88″ W. |
| ИСО 6709 | 1983 | Представление 7 десятичных цифр | Вариант, основанный на представлении XML, где структура данных представляет собой «кортеж, состоящий из широты и долготы, представляет двумерное географическое положение» , а каждое число в кортеже представляет собой действительное число, дискретизированное с помощью 7 десятичных знаков. Пример: 38.889475, -77.035244. |
| Код карты | 2001 – Апач2 | оригинальный | Первым, кто принял смешанный код в сочетании с кодами ISO 3166 (страна или город). В 2001 году алгоритмы получили лицензию Apache2, что обеспечивает выдачу патента. |
| Геохэш | 2008 – СС0 | оригинальный | Похожа на latLong с чересстрочной разверткой, и результат представляется в формате base32 . |
| Геохэш-36 | 2011 – СС0 | оригинальный | Несмотря на похожее название, не использует тот же алгоритм, что и Geohash . Использует сетку 6 на 6 и присваивает каждой ячейке букву. |
| Что3слова | запатентовано в 2013 г. | оригинальный (английский) | преобразует квадраты 3х3 метра в 3 слова из английского словаря. [30] |
| ПлюсКод | 2014 – Апач2 [31] | оригинальный | Также называется «Код открытого местоположения». Коды представляют собой числа в кодировке Base20 и могут использовать названия городов, уменьшая код на размер кода ограничивающего прямоугольника города (как в стратегии Mapcode). Пример: 87C4VXQ7+QV. |
| S2 Идентификатор ячейки /Base32 | 2015 – Апач2 [32] | исходное 64-битное целое число, выраженное в формате base32 | Иерархическая и очень эффективная индексация базы данных, но нет стандартного представления для base32 и префиксов городов, как PlusCode. |
| What3words /otherLang | 2016...2017 – запатентовано | другие языки | то же, что и английский, но в качестве справочника для слов используется другой словарь. Пример португальского языка и ячейка 10x14 м: tenaz.fatual.davam. |
Другие документированные системы:
| Имя DGG | Начало – лицензия | Краткое содержание | Описание |
|---|---|---|---|
| C-квадраты | 2003 – «Без ограничений». | Латлонг чересстрочный | Десятичное переплетение представления широты и долготы ISO с дополнительными идентификаторами для промежуточных квадрантов. Это «наивный» алгоритм по сравнению с двоичным чересстрочным преобразованием или Geohash. |
| ГЕОРЕФ | ~1990 – CC0 | Основан на ISO LatLong, но использует более простые и краткие обозначения. | «Мировая географическая справочная система», военная / аэронавигационная система координат для идентификации точек и территорий. |
| РЕБЯТА | 2007 г. – ограничено | США/ЭТО | Справочная система, разработанная Национальным агентством геопространственной разведки (NGA). «Стандартизированная система координат зоны боевых действий в Министерстве обороны, которая повлияет на весь спектр устранения конфликтов на боевом пространстве» |
| Квадраты ВМО | 2001.. – CC0? | специализированный | Ячейки загрузки изображений NOAA. ... делит карту мира с линиями сетки широты и долготы на ячейки сетки размером 10 ° широты и 10 ° долготы, каждая из которых имеет уникальный четырехзначный цифровой идентификатор. Прямоугольные ячейки 36x18 (обозначены четырьмя цифрами, первая цифра обозначает квадранты СВ/ЮВ/ЮЗ/СЗ). |
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Jump up to: а б с д Сахр, Кевин; Уайт, Денис; Кимерлинг, Эй Джей (2003). «Геодезические дискретные глобальные сеточные системы» (PDF) . Картография и географическая информатика . 30 (2): 121–134. дои : 10.1559/152304003100011090 . S2CID 16549179 .
- ^ Jump up to: а б Сахр, Кевин; Уайт, Денис; Кимерлинг, AJ (18 марта 1997 г.), «Предлагаемые критерии оценки дискретных глобальных сетей» , проект технического отчета , Корваллис, Орегон: Университет штата Орегон, заархивировано из оригинала 3 марта 2016 г. , получено 10 сентября 2014 г.
- ^ Джеффри Даттон. «Что такого особенного в глобальной иерархической тесселяции?» .цитата: «несколько систем-прототипов, которые представляют собой либо иерархическую мозаику, либо глобальную мозаику, либо и то, и другое».
- ^ «Обзор» .
- ^ «Глобальная высота 30 угловых секунд (GTOPO30)» . Геологическая служба США. Архивировано из оригинала 10 июля 2017 года . Проверено 8 октября 2015 г.
- ^ «Глобальные данные о высоте местности в разных разрешениях, 2010 г. (GMTED2010)» . Геологическая служба США . Проверено 8 октября 2015 г.
- ^ Аракава, Акио; Лэмб, Вивиан Р. (1977). «Вычислительное моделирование основных динамических процессов модели общей циркуляции Калифорнийского университета в Лос-Анджелесе». Модели общей циркуляции атмосферы . Методы вычислительной физики: достижения в исследованиях и приложениях. Том. 17. стр. 173–265. дои : 10.1016/B978-0-12-460817-7.50009-4 . ISBN 978-0-12-460817-7 .
- ^ «Научно-исследовательский институт квадратов мировой сетки» . Иокогамский городской университет . Проверено 21 ноября 2017 г.
- ^ Снайдер, JP (1992). «Равновеликая картографическая проекция для многогранных глобусов». Картографика . 29 (1): 10–21. дои : 10.3138/27h7-8k88-4882-1752 .
- ^ Барнс, Ричард (2019). «Оптимальные ориентации дискретных глобальных сетей и полюса недоступности». Международный журнал цифровой Земли . 13 (7): 803–816. дои : 10.1080/17538947.2019.1576786 . S2CID 134622203 .
- ^ Мартин Зюсс, Педро Матос (2004). «Обработка данных SMOS уровня 1С на дискретной глобальной сетке». Международный IEEE Международный IEEE Международный симпозиум IEEE по геонаукам и дистанционному зондированию, 2004 г. IGARSS '04. Слушания. 2004 . Том. 3. стр. 1914–1917. дои : 10.1109/IGARSS.2004.1370716 . ISBN 978-0-7803-8742-3 . S2CID 7267254 .
- ^ «Понимание глобальных сетевых систем» . Глобальные грид-системы. Архивировано из оригинала 16 ноября 2020 года . Проверено 8 октября 2015 г.
- ^ «LAMBDA - Четырехсторонний сферический куб COBE» .
- ^ Даттон, Джеффри Х. (1999). Иерархическая система координат для геообработки и картографии . Конспекты лекций по наукам о Земле. Том. 79. дои : 10.1007/BFb0011617 . ISBN 978-3-540-64980-9 . [ нужна страница ]
- ^ Снайдер, Ван (10 августа 2016 г.). «Четвертичная треугольная сетка: иерархическая система координат для геообработки и картографии». hdl : 2014/46916 .
{{cite journal}}: Для цитирования журнала требуется|journal=( помощь ) - ^ «Фоновая цель HEALPix» . Лаборатория реактивного движения НАСА . Проверено 8 октября 2015 г. .
- ^ «Ячейки S2» . Архивировано из оригинала 20 октября 2020 г. Проверено 06 сентября 2018 г.
- ^ «Обзор HTM» .
- ^ «Материалы конференции ADASS 2003» .
- ^ «S2 Геометрия» .
- ^ «Обзор» . s2geometry.io . Проверено 11 мая 2018 г.
- ^ Крайсс, Свен (27 июля 2016 г.). «Ячейки S2 и кривые, заполняющие пространство: ключ к созданию более эффективных инструментов цифровых карт для городов» . Середина . Проверено 11 мая 2018 г.
- ^ «Статистика ячеек S2» .
- ^ Jump up to: а б Открытый геопространственный консорциум (2017), «Тема 21: Абстрактная спецификация дискретных глобальных грид-систем». Документ 15-104р5 версия 1.0 .
- ^ Раздел 6.1, «Обзор базовой модели данных DGGS», стандарта DGGS.
- ^ Садурни, Р.; Аракава, А.; Минц, Ю. (1968). «Интегрирование недивергентного уравнения баротропной завихренности с икосаэдрально-гексагональной сеткой для сферы». Ежемесячный обзор погоды . 96 (6): 351–356. Бибкод : 1968MWRv...96..351S . CiteSeerX 10.1.1.395.2717 . doi : 10.1175/1520-0493(1968)096<0351:iotnbv>2.0.co;2 .
- ^ Уильямсон, Д.Л. (1968). «Интегрирование уравнения баротропной завихренности на сферической геодезической сетке». Теллус . 20 (4): 642–653. дои : 10.1111/j.2153-3490.1968.tb00406.x .
- ^ Кляйнер, Андреас; Брассель, Курт Э. (1986). «Иерархические сетчатые структуры для статических баз географических данных» (PDF) . В Блейкморе, Майкл (ред.). Auto Carto London: материалы Международной конференции по сбору, управлению и представлению пространственных данных, 14–19 сентября 1986 г. Авто Карто Лондон. стр. 485–496. ISBN 978-0-85406-312-3 . OCLC 898826374 .
- ^ Ян, Джин; Сун, Сяо; Гун, Гуанхун (2016). «Усредненное соотношение между дополнительными профилями для оценки искажений формы картографических проекций и сферических иерархических мозаик». Компьютеры и геонауки . 87 : 41–55. Бибкод : 2016CG.....87...41Y . дои : 10.1016/j.cageo.2015.11.009 .
- ^ «What3words: находите и делитесь очень точными местоположениями с помощью Google Maps, используя всего 3 слова» . 02 июля 2013 г. Проверено 8 июля 2014 г.
- ^ «Open Location Code — это библиотека для создания коротких кодов, которые можно использовать как уличные адреса, для мест, где уличные адреса не существуют.: Google/open-location-code» . Гитхаб . 18 февраля 2019 г.
- ^ «Вычислительная геометрия и пространственная индексация на сфере: Google/s2geometry» . Гитхаб . 18 февраля 2019 г.
Внешние ссылки
[ редактировать ]- OGC DGGS Рабочая группа по стандартам
- Страница дискретных глобальных сетей на факультете компьютерных наук Университета Южного Орегона
- Климатическая модель BUGS. Архивировано 15 декабря 2006 г. на странице Wayback Machine, посвященной геодезическим сеткам.
- Страница квадратов Исследовательского института мировой сетки на странице World Grid Squares
- Кубический почтовый индекс - действительный протокол для международной системы почтовых индексов, использующий сетку кубических метров.
- Модели земной сетки для выставочного использования . Модели некоторых земных решеток для 3D-печати.