Возмущение (астрономия)

Возмущающие силы Солнца на Луне в двух местах ее орбиты . Синие стрелки обозначают направление и величину гравитационной силы на Земле . Применение этого принципа как к положению Земли, так и к положению Луны не нарушает их положения относительно друг друга. Когда ее вычитают из силы, действующей на Луну (черные стрелки), остается возмущающая сила (красные стрелки) на Луне относительно Земли. Поскольку возмущающая сила различна по направлению и величине на противоположных сторонах орбиты, она вызывает изменение формы орбиты.

В астрономии на которое действуют силы , возмущение — это сложное движение массивного тела, отличные от гравитационного притяжения другого массивного тела . Другие силы могут включать третье (четвертое, пятое и т. д.) тело, сопротивление , как со стороны атмосферы , и нецентральное притяжение сплюснутого или иным образом деформированного тела.

Введение

Изучение возмущений началось с первых попыток предсказать движения планет на небе. В древние времена причины были неизвестны. Исаак Ньютон , когда он сформулировал свои законы движения и гравитации , применил их к первому анализу возмущений, осознавая сложные трудности их расчета. С тех пор многие великие математики уделяли внимание различным связанным с этим проблемам; На протяжении 18—19 вв. существовала потребность в точных таблицах положения Луны и планет для морской навигации .

Сложные движения гравитационных возмущений можно разрушить. Гипотетическое движение, которому тело следует только под действием гравитации другого тела, представляет собой коническое сечение и может быть описано в геометрических терминах. Это называется задачей двух тел или невозмущенной кеплеровской орбитой . Различия между этим и реальным движением тела представляют собой возмущения, вызванные дополнительными гравитационными эффектами оставшегося тела или тел. Если есть только еще одно значимое тело, то возмущенное движение представляет собой задачу трех тел ; если есть несколько других тел, это n проблема тел . Общее аналитическое решение (математическое выражение для прогнозирования положений и движений в любой момент времени) существует для задачи двух тел; когда рассматривается более двух тел, аналитические решения существуют только для особых случаев. Даже задача двух тел становится неразрешимой, если одно из тел имеет неправильную форму.

Орбитальная долгота и широта Меркурия , возмущенная Венерой , Юпитером и всеми планетами Солнечной системы с интервалом в 2,5 дня. Меркурий оставался бы в центре перекрестия, если бы не было возмущений.

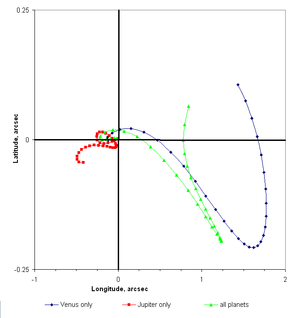
Большинство систем, в которых присутствует множественное гравитационное притяжение, представляют собой одно первичное тело, которое доминирует в своих воздействиях (например, звезда в случае звезды и ее планеты или планета в случае планеты и ее спутника). Гравитационное воздействие других тел можно трактовать как возмущения гипотетического невозмущенного движения планеты или спутника вокруг своего основного тела.

Математический анализ

Общие возмущения

В методах общих возмущений общие дифференциальные уравнения движения или изменения элементов орбит решаются аналитически, обычно путем разложения в ряд . Результат обычно выражают через алгебраические и тригонометрические функции элементов орбит рассматриваемого тела и возмущающих тел. В целом это можно применить ко многим различным наборам условий и не относится конкретно к какому-либо конкретному набору гравитирующих объектов. Исторически сложилось так, что в первую очередь исследовались общие возмущения. Классические методы известны как вариация элементов , вариация параметров или вариация констант интегрирования . В этих методах считается, что тело всегда движется в коническом сечении , однако коническое сечение постоянно изменяется из-за возмущений. Если бы все возмущения прекратились в какой-то конкретный момент, тело продолжало бы находиться в этом (теперь неизменном) коническом сечении бесконечно; эта коника известна как соприкасающаяся орбита , и ее орбитальные элементы в любой конкретный момент времени являются тем, что ищут методами общих возмущений.

Общие возмущения используют тот факт, что во многих задачах небесной механики орбита двух тел изменяется из-за возмущений довольно медленно; орбита двух тел является хорошим первым приближением. Общие возмущения применимы только в том случае, если возмущающие силы примерно на порядок меньше или меньше силы гравитации основного тела. В Солнечной системе это обычно так; Юпитер , второе по величине тело, имеет массу около 1/1000 ​ ​ солнечной ​ .

Для некоторых типов задач предпочтительны общие методы возмущений, поскольку легко найти источник определенных наблюдаемых движений. Это не обязательно так для особых возмущений; движения были бы предсказаны с такой же точностью, но не было бы никакой информации о конфигурациях возмущающих тел (например, орбитальный резонанс ), вызвавших их.

Особые возмущения

В методах специальных возмущений наборы числовых данных, представляющие значения положений, скоростей и ускоряющих сил на интересующие тела, составляют основу численного интегрирования дифференциальных уравнений движения . Фактически, положения и скорости изменяются напрямую, и не предпринимается никаких попыток вычислить кривые орбит или элементов орбит .

Специальные возмущения могут быть применены к любой задаче небесной механики , поскольку она не ограничивается случаями, когда возмущающие силы малы. Специальные методы возмущений, которые когда-то применялись только к кометам и малым планетам, теперь лежат в основе самых точных машинно генерируемых планетарных эфемерид великих астрономических альманахов. Специальные возмущения также используются для моделирования орбиты с помощью компьютеров.

Формулировка Коуэлла

Метод Коуэлла. Силы всех возмущающих тел (черного и серого) суммируются, образуя общую силу, действующую на тело. $\ i\$ (красный), и это численно интегрировано, начиная с исходного положения ( эпоха соприкосновения ).

Формулировка Коуэлла (названная так в честь Филипа Х. Коуэлла , который вместе с ACD Cromellin использовал аналогичный метод для предсказания возвращения кометы Галлея), возможно, является самым простым из специальных методов возмущений. В системе $\ n\$ взаимодействующих тел, этот метод математически определяет силы Ньютона , действующие на тело. $\ i\$ суммируя отдельные взаимодействия друг с другом $j$ тела:

$\mathbf {\ddot {r}} _{i}=\sum _{\underset {j\neq i}{j=1}}^{n}\ G\ m_{j}{\frac {\ (\mathbf {r} _{j}-\mathbf {r} _{i})\ }{\ \|\mathbf {r} _{j}-\mathbf {r} _{i}\|^{3}}}$

где $\ \mathbf {\ddot {r}} _{i}\$ вектор ускорения тела $i$, $G$ гравитационная постоянная , $\ m_{j}\$ это масса тела $j$, $\ \mathbf {r} _{i}\$ и $\ \mathbf {r} _{j}\$ — векторы положения объектов $\ i\$ и $\ j\$ соответственно, и $\ r_{ij}\equiv \|\mathbf {r} _{j}-\mathbf {r} _{i}\|\$ это расстояние от объекта $i$ возражать $\ j\$, причем все векторы отнесены к барицентру системы. Это уравнение разлагается на компоненты $\ x\ ,$ $\ y\ ,$ и $\ z\ ,$ и они численно интегрируются для формирования новых векторов скорости и положения. Этот процесс повторяется столько раз, сколько необходимо. Преимущество метода Коуэлла — простота применения и программирования. Недостаток состоит в том, что когда возмущения становятся большими по величине (например, когда объект приближается к другому), ошибки метода также становятся большими. Однако для многих задач небесной механики это не так. Другой недостаток состоит в том, что в системах с доминирующим центральным телом, таких как Солнце , приходится нести в арифметике много из значащих цифр -за большой разницы в силах центрального тела и возмущающих тел, хотя и с высокой точностью чисел. встроенное в современные компьютеры, это уже не такое большое ограничение, как раньше.

метод Энке

Метод Энке. Здесь сильно преувеличенная небольшая разница δ r (синий) между соприкасающейся невозмущенной орбитой (черный) и возмущенной орбитой (красный) численно интегрируется, начиная с исходного положения (эпоха соприкосновения ).

Метод Энке начинается с соприкасающейся орбиты в качестве эталона и численно интегрируется для определения отклонения от эталонной орбиты как функции времени. Его преимущества заключаются в том, что возмущения обычно невелики по величине, поэтому интегрирование может происходить более крупными шагами (с меньшими ошибками), и на метод гораздо меньше влияют экстремальные возмущения. Его недостатком является сложность; его нельзя использовать бесконечно, не обновляя время от времени соприкасающуюся орбиту и не продолжая оттуда - процесс, известный как выпрямление . Метод Энке аналогичен общему методу возмущений изменения элементов, за исключением того, что выпрямление выполняется через дискретные промежутки времени, а не непрерывно.

Сдача в аренду ${\boldsymbol {\rho }}$ быть радиус-вектором орбиты соприкасающейся , $\mathbf {r}$ радиус-вектор возмущенной орбиты и $\delta \mathbf {r}$ отклонение от соприкасающейся орбиты,

$\delta \mathbf {r} =\mathbf {r} -{\boldsymbol {\rho }}$, и движения уравнение $\delta \mathbf {r}$ это просто ( 1 )

${\ddot {\delta \mathbf {r} }}=\mathbf {\ddot {r}} -{\boldsymbol {\ddot {\rho }}}$. ( 2 )

$\mathbf {\ddot {r}}$ и ${\boldsymbol {\ddot {\rho }}}$ это просто уравнения движения $\mathbf {r}$ и ${\boldsymbol {\rho }},$

$\mathbf {\ddot {r}} =\mathbf {a} _{\text{per}}-{\mu \over r^{3}}\mathbf {r}$ для возмущенной орбиты и ( 3 )

${\boldsymbol {\ddot {\rho }}}=-{\mu \over \rho ^{3}}{\boldsymbol {\rho }}$ для невозмущенной орбиты, ( 4 )

где $\mu =G(M+m)$ гравитационный параметр с $M$ и $m$ массы , центрального тела и возмущенного тела $\mathbf {a} _{\text{per}}$ – возмущающее ускорение , а $r$ и $\rho$ являются величины $\mathbf {r}$ и ${\boldsymbol {\rho }}$.

Подставляя уравнения ( 3 ) и ( 4 ) в уравнение ( 2 ),

${\ddot {\delta \mathbf {r} }}=\mathbf {a} _{\text{per}}+\mu \left({{\boldsymbol {\rho }} \over \rho ^{3}}-{\mathbf {r} \over r^{3}}\right),$ ( 5 )

которое теоретически можно было бы проинтегрировать дважды, чтобы найти $\delta \mathbf {r}$. Поскольку соприкасающаяся орбита легко вычисляется методами двух тел, ${\boldsymbol {\rho }}$ и $\delta \mathbf {r}$ учитываются и $\mathbf {r}$ можно решить. На практике количество в скобках ${{\boldsymbol {\rho }} \over \rho ^{3}}-{\mathbf {r} \over r^{3}}$, представляет собой разницу двух почти равных векторов, и необходимы дальнейшие манипуляции, чтобы избежать необходимости использования дополнительных значащих цифр . Метод Энке более широко использовался до появления современных компьютеров , когда большая часть вычислений по орбитам выполнялась на механических вычислительных машинах .

Периодический характер

График Gravity Simulator изменения эксцентриситета орбит Меркурия Венеры , . , Земли и Марса в течение следующих 50 000 лет Точкой 0 на этом графике является 2007 год.

В Солнечной системе многие возмущения одной планеты другой носят периодический характер и состоят из небольших импульсов каждый раз, когда планета проходит по своей орбите другую. Это заставляет тела следовать периодическим или квазипериодическим движениям – например, Луна на ее сильно возмущенной орбите , что является предметом лунной теории . Этот периодический характер привел к открытию Нептуна в 1846 году в результате возмущений им орбиты Урана .

Продолжающиеся взаимные возмущения планет вызывают долгосрочные квазипериодические изменения элементов их орбит , наиболее очевидные, когда орбитальные периоды двух планет почти синхронизированы. Например, пять оборотов Юпитера (59,31 года) почти равны двум оборотам Сатурна (58,91 года). Это вызывает большие возмущения обоих с периодом 918 лет — время, необходимое для того, чтобы небольшая разница в их положениях при соединении совершила один полный круг, впервые обнаруженный Лапласом . Венера в настоящее время имеет орбиту с наименьшим эксцентриситетом , то есть она наиболее близка к круговой из всех планетарных орбит. Через 25 000 лет у Земли будет более круглая (менее эксцентричная) орбита, чем у Венеры. Было показано, что долговременные периодические возмущения в Солнечной системе могут стать хаотическими в очень длительных временных масштабах; при некоторых обстоятельствах одна или несколько планет могут пересечь орбиту другой, что приведет к столкновениям.

Орбиты многих малых тел Солнечной системы, таких как кометы , часто сильно возмущены, особенно гравитационными полями газовых гигантов . Хотя многие из этих возмущений являются периодическими, другие нет, и они, в частности, могут представлять собой аспекты хаотического движения . Например, в апреле 1996 года уменьшению гравитационное влияние Юпитера привело к периода обращения кометы Хейла-Боппа с 4206 до 2380 лет, и это изменение не вернется ни на какой периодической основе.

См. также

• Формирование и эволюция Солнечной системы
• Замороженная орбита
• Molniya orbit
• Нереида, один из внешних спутников Нептуна, с высоким эксцентриситетом орбиты ~ 0,75 и часто возмущается.
• Соприкасающаяся орбита
• Моделирование орбиты
• Орбитальный резонанс
• Собственные элементы орбиты
• Стабильность Солнечной системы

Ссылки

Библиография

• Бейт, Роджер Р.; Мюллер, Дональд Д.; Уайт, Джерри Э. (1971). Основы астродинамики . Нью-Йорк: Dover Publications . ISBN  0-486-60061-0 .
• Моултон, Форест Рэй (1914). Введение в небесную механику (2-е исправленное изд.). Макмиллан.
• Рой, А.Е. (1988). Орбитальное движение (3-е изд.). Институт физического издательства. ISBN  0-85274-229-0 .

Сноски

Дальнейшее чтение

• П.Э. Эль-Ясберг: Введение в теорию полета искусственных спутников Земли

Внешние ссылки

• Прогнозы Solex (Альдо Витальяно) относительно положения/орбиты/близких сближений Марса
• Гравитация. Книга сэра Джорджа Бидделла Эйри 1884 года о гравитационном движении и возмущениях, в которой практически не используется математика. (в книгах Google )