Лунная теория

Лунная теория пытается объяснить движение Луны . существует множество небольших вариаций (или возмущений В движении Луны ), и было предпринято множество попыток их объяснить. После столетий проблем движение Луны теперь можно моделировать с очень высокой степенью точности (см. раздел «Современные разработки »).

Лунная теория включает в себя:

• основы общей теории; включая математические методы, используемые для анализа движения Луны и создания формул и алгоритмов для прогнозирования ее движения; а также
• количественные формулы, алгоритмы и геометрические диаграммы, которые можно использовать для расчета положения Луны в заданный момент времени; часто с помощью таблиц на основе алгоритмов.

Теория Луны имеет историю исследований, насчитывающую более 2000 лет. Ее более современные разработки использовались на протяжении последних трех столетий для фундаментальных научных и технологических целей и используются до сих пор.

Приложения

Приложения теории Луны включали следующее:

• В восемнадцатом веке сравнение теории Луны с наблюдениями использовалось для проверки закона всемирного тяготения Ньютона путем движения апогея Луны .
• В XVIII и XIX веках навигационные таблицы, основанные на теории Луны, первоначально в « Морском альманахе» широко использовались для определения долготы на море методом лунных расстояний .
• В самом начале двадцатого века сравнение теории Луны с наблюдениями было использовано в другой проверке теории гравитации, чтобы проверить (и исключить) предположение Саймона Ньюкомба о том, что хорошо известное несоответствие в движении перигелия Меркурия может быть объясняется дробным изменением степени -2 в законе обратных квадратов гравитации Ньютона. (расхождение позднее было успешно объяснено общей теорией относительности ).
• В середине двадцатого века, до разработки атомных часов, теория Луны и наблюдения использовались в сочетании для реализации астрономической шкалы времени ( эфемеридного времени ), свободной от неравномерностей среднего солнечного времени.
• В конце двадцатого и начале двадцать первого века современные разработки теории Луны используются в «Эфемериды» Лаборатории реактивного движения серии моделей Солнечной системы в сочетании с высокоточными наблюдениями для проверки точности физических взаимосвязей, связанных с с общей теорией относительности , включая сильный принцип эквивалентности , релятивистскую гравитацию, геодезическую прецессию и постоянство гравитационной постоянной .

История

Луну наблюдали на протяжении тысячелетий. В течение этого возраста были возможны различные уровни осторожности и точности в зависимости от методов наблюдения, доступных в любое время. Соответственно, существует долгая история лунных теорий: она простирается от времен вавилонских и греческих астрономов до современной лунной лазерной локации.

Среди выдающихся астрономов и математиков прошлых веков, чьи имена связаны с лунными теориями, можно назвать:

Вавилонский/Халдейский

• Набуриманну
• Кидинну
• Судины

Греческий/эллинистический

• Гиппарх
• Птолемей

араб

• Ибн аль-Шатир

Европа, 16 - начало 20 веков.

• Тихо Браге
• Иоганнес Кеплер
• Джеремия Хоррокс
• Исмаэль Буллиалдус
• Джон Флемстид
• Исаак Ньютон
• Эдмонд Хэлли
• Леонард Эйлер
• Алексис Клеро
• Жан Даламбер
• Тобиас Майер
• Иоганн Тобиас Бюрг
• Пьер-Симон Лаплас
• Филипп ле Дульсе
• Иоганн Карл Буркхардт
• Питер Андреас Хансен
• Шарль-Эжен Делоне
• Джон Коуч Адамс

Северная Америка, 19 – начало 20 веков.

• Саймон Ньюкомб
• Джордж Уильям Хилл
• Эрнест Уильям Браун
• Уоллес Джон Эккерт

Другие известные математики и математические астрономы также внесли значительный вклад.

Можно считать, что историю можно разделить на три части: от древних времен до Ньютона; период классической (ньютоновской) физики; и современные разработки.

Древние времена Ньютона

Вавилон

О вавилонской астрономии историкам науки до 1880-х годов практически ничего не было известно. В сохранившихся древних сочинениях Плиния почти не упоминаются три астрономические школы в Месопотамии – в Вавилоне, Уруке и «Гиппарене» (возможно, «Сиппаре»). Но определенные современные знания о каких-либо деталях начались только тогда, когда Джозеф Эппинг расшифровал клинописные тексты на глиняных табличках из вавилонского архива: В этих текстах он определил эфемериды положений Луны. С тех пор знания по предмету, пока еще фрагментарные, приходилось формировать путем кропотливого анализа расшифрованных текстов, главным образом в числовой форме, на табличках из Вавилона и Урука (чего-либо из третьей школы, упомянутой еще Плиний).

Вавилонскому постоянно астроному Кидинну (по-гречески или по-латински Киденас или Киденас) приписывают изобретение (5 или 4 век до н.э.) того, что сейчас называется «Системой Б», для предсказания положения Луны, принимая во внимание, что Луна меняет свою скорость на своем пути относительно фона неподвижных звезд. Эта система включала ежедневный расчет ступенчатых изменений скорости Луны в большую или меньшую сторону с минимумом и максимумом примерно каждый месяц. Основой этих систем, по-видимому, была скорее арифметическая, чем геометрическая, но они приблизительно объясняли главное лунное неравенство, теперь известное как уравнение центра .

Вавилоняне в течение сотен лет вели очень точные записи новолуний и затмений. Где-то между 500 и 400 годами до нашей эры они определили и начали использовать 19-летнюю циклическую связь между лунными месяцами и солнечными годами, известную теперь как цикл Метона .

Это помогло им построить численную теорию основных неравномерностей движения Луны, получив удивительно хорошие оценки для (различных) периодов трех наиболее ярких особенностей движения Луны:

• Синодический месяц, то есть средний период фаз Луны. Теперь называемая «Системой Б», она считает синодический месяц равным 29 дням и (шестидесятеричным) 3,11;0,50 «градуса времени», где каждый градус времени видимого движения звезд, или 4 минутам равен одному градусу время, а шестидесятеричные значения после точки с запятой представляют собой доли градуса времени. Это преобразуется в 29,530594 дня = 29. ^д  12 ^час  44 ^м  3.33 ^с , для сравнения с современным значением (по состоянию на 0 января 1900 г.) 29,530589 дней, или 29 ^д  12 ^час  44 ^м  2.9 ^с . Это же значение использовалось Гиппархом и Птолемеем, использовалось на протяжении всего Средневековья и до сих пор составляет основу еврейского календаря .
• Средняя скорость Луны относительно звезд, по их оценкам, составила 13°10′35″ в день, что дает соответствующий месяц в 27,321598 дней. для сравнения с современными значениями 13°10′ 35,0275″ и 27,321582 суток.
• Аномалистический месяц, то есть средний период примерно ежемесячных ускорений и замедлений скорости движения Луны относительно звезд, имел вавилонскую оценку 27,5545833 дня, для сравнения с современным значением 27,554551 дня.
• Драконический месяц, то есть средний период, с которым путь Луны относительно звезд отклоняется сначала на север, а затем на юг в эклиптической широте по сравнению с эклиптическим путем Солнца, был указан рядом различных параметров, приводящих к различным оценкам. например, 27,212204 дня, для сравнения с современным значением 27,212221, но у вавилонян была еще и числовая зависимость, согласно которой 5458 синодических месяцев равнялись 5923 драконитским месяцам, что при сравнении с их точным значением для синодического месяца приводит практически к современной цифре для драконитного месяца.

Вавилонская оценка синодического месяца была принята на протяжении большей части двух тысячелетий Гиппархом, Птолемеем и средневековыми авторами (и до сих пор используется как часть основы для расчета еврейского (еврейского) календаря ).

Греция и эллинистический Египет

После этого, начиная с Гиппарха и Птолемея в вифинскую и птолемеевскую эпохи и вплоть до времен Ньютона в семнадцатом веке, лунные теории создавались главным образом с помощью геометрических идей, вдохновленных более или менее непосредственно длинными сериями позиционных наблюдений за луной. луна. Видное место в этих геометрических теориях Луны занимали комбинации круговых движений – приложения теории эпициклов .

Гиппарх

См. Также: Гиппарх: Орбита Луны.

Гиппарх , работы которого большей частью утеряны и известны главным образом по цитатам других авторов, предполагал, что Луна двигалась по кругу, наклоненному под 5° к эклиптике , вращаясь в ретроградном направлении (т.е. противоположном направлению годовых и месячных видимых движений Луны). Солнца и Луны относительно неподвижных звезд) один раз из 18 2 ⁄ года . Круг выполнял функцию отводящего круга , несущего эпицикл, по которому предполагалось движение Луны в ретроградном направлении. Центр эпицикла перемещался со скоростью, соответствующей среднему изменению долготы Луны, а период обращения Луны вокруг эпицикла был аномалистическим месяцем. Этот эпицикл примерно обеспечивал то, что позже было признано эллиптическим неравенством, уравнением центра , а его размер приближался к уравнению центра около 5°1'. Эта цифра гораздо меньше современного значения : но она близка к разнице между современными коэффициентами уравнения центра (1-го члена) и коэффициентом выталкивания : разница объясняется тем, что древние измерения были снятые во время затмений, и эффект выброса (который вычитается в этих условиях из уравнения центра) был в то время неизвестен и упускался из виду. Дополнительную информацию см. также в отдельной статье Evection .

Птолемей

Альмагест Работа Птолемея « » пользовалась широким и продолжительным признанием и влиянием на протяжении более тысячелетия. Он предложил геометрическую лунную теорию, которая улучшила теорию Гиппарха, предусмотрев второе неравенство движения Луны, используя устройство, которое заставляло видимый апогей немного колебаться - просневис эпицикла. Это второе неравенство , или вторая аномалия , довольно приблизительно объясняло не только уравнение центра, но и то, что стало известно (много позже) как выталкивание . Но эта теория, если применить ее к своему логическому завершению, приведет к тому, что расстояние (и видимый диаметр) Луны изменится примерно в 2 раза, чего явно не наблюдается в действительности. (Видимый угловой диаметр Луны действительно меняется ежемесячно, но только в гораздо более узком диапазоне — около 0,49°–0,55°. ) Этот дефект теории Птолемеев привел к тому, что Ибн аль-Шатир в 14 веке предложил замену. и Коперником в 16 веке.

Ибн аль-Шатир и Коперник

Значительных успехов в теории Луны добился астроном арабский Ибн аль-Шатир (1304–1375). Основываясь на наблюдении, что расстояние до Луны не изменилось так радикально, как того требовала лунная модель Птолемея, он создал новую лунную модель, которая заменила кривошипно-шатунный механизм Птолемея моделью двойного эпицикла, которая уменьшила вычисленный диапазон расстояний Луны от Луны. Земля. Похожая лунная теория, разработанная около 150 лет спустя астрономом Возрождения эпохи Николаем Коперником , имела такое же преимущество в отношении лунных расстояний.

Кеплер и

Тихо Браге и Иоганнес Кеплер усовершенствовали лунную теорию Птолемея, но не преодолели ее главный недостаток, заключающийся в плохом учете (в основном ежемесячных) изменений расстояния до Луны, видимого диаметра и параллакса . Их работа добавила к теории Луны еще три существенных открытия.

1. Узлы и наклон плоскости лунной орбиты, по-видимому , либрируют с месячным (согласно Тихо) или полугодовым периодом (согласно Кеплеру).
2. Лунная долгота имеет изменение два раза в месяц , при котором Луна движется быстрее, чем ожидалось, в новолуние и полнолуние и медленнее, чем ожидалось, в четверти луны.
3. Существует также годовой эффект, благодаря которому движение Луны немного замедляется в январе и немного ускоряется в июле: годовое уравнение .

Уточнения Браге и Кеплера были признаны их непосредственными преемниками как усовершенствования, но их преемники в семнадцатом веке попробовали многочисленные альтернативные геометрические конфигурации движения Луны, чтобы еще больше улучшить ситуацию. Заметного успеха добился Иеремия Хоррокс , предложивший схему, предполагающую примерно 6-месячную либрацию положения апогея Луны, а также величины эллиптического эксцентриситета. Эта схема имела большое достоинство, поскольку давала более реалистичное описание изменений расстояния, диаметра и параллакса Луны.

Ньютон

Первый гравитационный период теории Луны начался с работы Ньютона . Он был первым, кто определил проблему возмущенного движения Луны в узнаваемых современных терминах. Его новаторские работы показаны, например, в Principia. во всех версиях, включая первое издание, опубликованное в 1687 году.

Биограф Ньютона, Дэвид Брюстер , сообщил, что сложность теории Луны повлияла на здоровье Ньютона: «[Он] был лишен аппетита и сна» во время работы над проблемой в 1692–1693 годах, и рассказал астроному Джону Мачину, что «его голова никогда не болела, кроме как когда он изучал предмет». По словам Брюстера, Эдмунд Галлей также рассказал Джону Кондуитту , что, когда его просили завершить анализ, Ньютон «всегда отвечал, что от этого у него болит голова и что он так часто не дает спать, что он больше не думает об этом » [курсив в оригинале].

движения

Ньютон определил, как оценить возмущающее воздействие на относительное движение Земли и Луны, возникающее из-за их гравитации по отношению к Солнцу, в Книге 1, Предложение 66: и в книге 3, предложение 25. Отправной точкой этого подхода является следствие VI законов движения. Это показывает, что если внешние ускоряющие силы со стороны некоторого массивного тела будут действовать одинаково и параллельно на некоторые другие рассматриваемые тела, то на эти тела будут воздействовать одинаково, и в этом случае их движения (относительно друг друга) будут продолжаться, как если бы таких внешних ускоряющих сил вообще не было. Только в том случае, если внешние силы (например, в книге 1, положение 66 и в книге 3, положение 25 — гравитационное притяжение к Солнцу) различны по величине или по направлению в своем ускоряющем воздействии на разные тела. считали (например, на Земле и Луне), что на относительные движения последних тел заметны последовательные воздействия. (Ньютон имел в виду ускоряющие силы или ускоряющую гравитацию, возникающую из-за какого-то внешнего массивного аттрактора, такого как Солнце. Мерой, которую он использовал, было ускорение, которое эта сила имеет тенденцию создавать (в современных терминах, сила на единицу массы), а не то, что мы бы сейчас вызовите сами силы.)

Таким образом, Ньютон пришел к выводу, что только разница между ускоряющимся притяжением Солнца к Луне и притяжением Солнца к Земле возмущает движение Луны относительно Земли.

Тогда Ньютон фактически использовал векторное разложение сил: провести этот анализ. В книге 1, предложение 66 и в книге 3, предложение 25, он показал с помощью геометрической конструкции, исходя из полного гравитационного притяжения Солнца к Земле и Солнца к Луне, разницу, которая представляет собой возмущающее воздействие на движение Луны относительно Земли. Таким образом, линия LS на диаграмме Ньютона, как показано ниже, представляет величину и направление возмущающего ускорения, действующего на Луну в текущем положении Луны P (линия LS не проходит через точку P, но текст показывает, что это не предназначено для быть значительным, это результат масштабных факторов и способа построения диаграммы).

Диаграмма Ньютона «найти силу Солнца, возмущающую Луну», сопровождающая Книгу 3, Предложение 25 «Начал ».

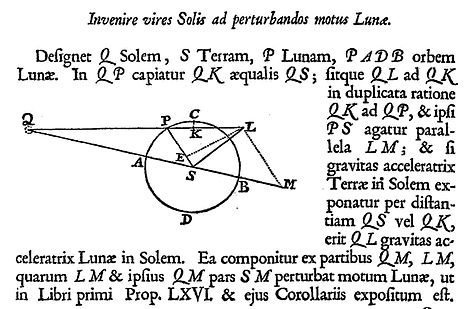
Здесь показана диаграмма Ньютона из первого (1687 г.) латинского издания « Начал» (книга 3, предложение 25, стр. 434). Здесь он представил свой анализ возмущающих ускорений на Луне в системе Солнце-Земля-Луна. Q представляет Солнце, S — Землю, а P — Луну.

Части этой диаграммы представляют расстояния, другие части — гравитационные ускорения (силы притяжения на единицу массы). В двойном значении SQ представляет расстояние Земля-Солнце, а также размер и направление гравитационного ускорения Земли-Солнца. Остальные расстояния на диаграмме тогда пропорциональны расстоянию SQ. Остальные достопримечательности пропорциональны привлекательности SQ.

Притяжения Солнца — SQ (на Земле) и LQ (на Луне). Размер LQ нарисован так, чтобы отношение притяжений LQ:SQ было обратным квадрату отношения расстояний PQ:SQ. (Ньютон строит KQ=SQ, что облегчает представление о пропорциях.) Притяжение Земли к Луне действует в направлении PS. (Но линия PS до сих пор обозначает только расстояние и направление, а о масштабном коэффициенте между солнечными и земными притяжениями ничего не определено).

Показав в одном масштабе солнечные притяжения LQ на Луне и SQ на Земле, Ньютон затем производит векторное разложение LQ на компоненты LM и MQ. Затем он определяет возмущающее ускорение на Луне как отличие этого от SQ. SQ и MQ параллельны друг другу, поэтому SQ можно напрямую вычесть из MQ, оставив MS. Таким образом, полученная разница после вычитания SQ из LQ представляет собой векторную сумму LM и MS: они в сумме дают возмущающее ускорение LS.

Позже Ньютон определил другое разделение возмущающего ускорения LM+MS = LS на ортогональные компоненты: поперечный компонент, параллельный LE, и радиальный компонент, фактически ES.

Альтернативное изображение солнечных возмущений, векторов LS1 и LS2, как LS на диаграмме Ньютона выше, для двух положений Луны P на ее орбите вокруг Земли S.

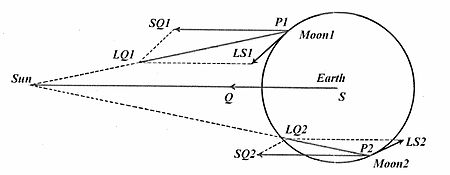
Схематическая схема Ньютона с тех пор была представлена ​​в других и, возможно, визуально более ясных формах. Здесь представлена ​​векторная презентация. указывая для двух разных положений Луны на ее орбите вокруг Земли, P1 и P2, соответствующие векторы LS1 и LS2 для возмущающего ускорения, вызываемого Солнцем. Положение Луны в точке P1 довольно близко к тому, что было в точке P на диаграмме Ньютона; соответствующее возмущение LS1 похоже на LS Ньютона по размеру и направлению. В другом положении P2 Луна находится дальше от Солнца, чем Земля, притяжение Солнца LQ2 к Луне слабее, чем притяжение Солнца SQ=SQ2 к Земле, и тогда результирующее возмущение LS2 направлено под углом от Солнца. .

Векторы солнечных возмущений (стрелки), аналогичные LS во многих положениях Луны на ее орбите вокруг Земли.

Конструкции, подобные тем, что изображены на диаграмме Ньютона, можно повторить для многих различных положений Луны на ее орбите. Для каждой позиции результатом является вектор возмущения, подобный LS1 или LS2 на второй диаграмме. Здесь показана часто представляемая форма диаграммы, которая суммирует размеры и направления векторов возмущений для многих различных положений Луны на ее орбите. Каждая маленькая стрелка представляет собой вектор возмущения, подобный LS, применимый к Луне в определенном положении вокруг орбиты, с которой начинается стрелка. Возмущения на Луне, когда она почти совпадает с осью Земля-Солнце, т.е. вблизи новолуния или полнолуния, направлены наружу, в сторону от Земли. Когда линия Луна-Земля находится под углом 90° от оси Земля-Солнце, они направлены внутрь, к Земле, с размером, составляющим лишь половину максимального размера осевых (наружных) возмущений. (Ньютон дал довольно хорошую количественную оценку размера солнечной возмущающей силы: в квадратуре , где она усиливает притяжение Земли, он определил ее как 1 / 178,725 среднего земного притяжения и вдвое больше, чем в новолуния и полнолуния, где оно противодействует земному притяжению и уменьшает его.)

Ньютон также показал, что та же самая закономерность возмущений применима не только к Луне в ее отношении к Земле, возмущенной Солнцем, но и к другим частицам в более общем плане в их отношении к твердой Земле, возмущенной Солнцем (или по Луне); например, различные части приливных вод на поверхности Земли. Изучение общей закономерности этих возмущающих ускорений выросло из первоначального исследования Ньютоном возмущений Луны, которое он также применил к силам, перемещающим приливные воды. В настоящее время этот общий образец сам по себе стал часто известен как приливная сила , независимо от того, применяется ли он к возмущениям движения Луны или приливных вод Земли – или к движениям любого другого объекта, который испытывает возмущения аналогичного характера.

После представления своей диаграммы «чтобы найти силу Солнца, возмущающую Луну» в Книге 3, Предложение 25, Ньютон разработал первое приближение к солнечной возмущающей силе, показав более подробно, как ее компоненты изменяются по мере того, как Луна следует своему месячному пути. вокруг Земли. Он также сделал первые шаги в исследовании того, как возмущающая сила проявляет свое воздействие, создавая неравномерности в движении Луны.

Для некоторых избранных лунных неравенств Ньютон показал в некоторых количественных деталях, как они возникают из-за солнечной возмущающей силы.

Большая часть лунных работ Ньютона была выполнена в 1680-х годах, и масштабы и точность его первых шагов в гравитационном анализе были ограничены несколькими факторами, включая его собственный выбор развивать и представлять работу в том виде, в котором, в целом, сложным геометрическим способом, а также ограниченной точностью и неопределенностью многих астрономических измерений его времени.

гравитационный период

Главной целью преемников Ньютона, от Леонарда Эйлера , Алексиса Клеро и Жана Даламбера в середине восемнадцатого века до Эрнеста Уильяма Брауна в конце девятнадцатого и начале двадцатого века, было полное и гораздо более точное объяснение лунного движения. движения на основе законов Ньютона, т. е. законов движения и всемирного тяготения за счет притяжения, обратно пропорционального квадратам расстояний между притягивающими телами. Они также хотели проверить закон обратных квадратов тяготения, и какое-то время в 1740-х годах он подвергался серьезным сомнениям из-за того, что тогда считалось большим расхождением между ньютоновскими и наблюдаемыми скоростями гравитации. движение лунного апогея. Однако вскоре после этого (1749–1750 гг.) Клеро показал , что, по крайней мере, основная причина расхождения лежит не в теории Луны, основанной на законах Ньютона, а в чрезмерных приближениях, на которые он и другие полагались для ее оценки.

Большинство усовершенствований в теории после Ньютона были сделаны в алгебраической форме: они включали объемные и весьма трудоемкие расчеты бесконечно малых и тригонометрию. Оставалось также для завершения теорий этого периода обратиться к наблюдательным измерениям.

теорий

Теоретики Луны использовали (и изобрели) множество различных математических подходов для анализа проблемы гравитации. Неудивительно, что их результаты имели тенденцию к сближению. Со времен первых гравитационных аналитиков среди преемников Ньютона, Эйлера , Клеро и Даламбера , было признано, что почти все основные лунные возмущения можно выразить с помощью всего лишь нескольких угловых аргументов и коэффициентов. Они могут быть представлены:

• средние движения или положения Луны и Солнца вместе с тремя коэффициентами и тремя угловыми положениями, которые вместе определяют форму и расположение их видимых орбит:
• два эксцентриситета ( $e$, около 0,0549, и $e'$, около 0,01675) эллипсов, приближающихся к видимым орбитам Луны и Солнца;
• угловое направление перигеев ( $\Gamma$ и $\Gamma '$) (или их противоположные точки — апогеи) двух орбит; и
• угол наклона ( $i$, среднее значение около 18523") между плоскостями двух орбит вместе с направлением ( $\Omega$) линии узлов, в которой пересекаются эти две плоскости. Восходящий узел ( $\Omega$) — узел, пройденный Луной, когда она стремится к северу относительно эклиптики.

Из этих основных параметров достаточно всего четырех основных дифференциальных угловых аргументов, чтобы выразить в их различных комбинациях почти все наиболее значительные возмущения лунных движений. Здесь они даны со своими условными символами, принадлежащими Делоне ; их иногда называют аргументами Делоне:

• $l$ средняя аномалия Луны (угловое расстояние средней долготы Луны от средней долготы ее перигея $\Gamma$);
• $l'$ средняя аномалия Солнца (угловое расстояние средней долготы Солнца от средней долготы его перигея $\Gamma '$);
• $F$ средний аргумент широты Луны (угловое расстояние средней долготы Луны от средней долготы ее восходящего (направленного на север) узла $\Omega$);
• $D$ средняя (солнечная) удлиненность Луны (угловое расстояние средней долготы Луны от средней долготы Солнца).

Кульминацией этой работы стала теория Луны Брауна (1897–1908). и Таблицы движения Луны (1919). Они использовались в Американских эфемеридах и Морском альманахе до 1968 года, а в измененной форме — до 1984 года.

лунные

Названы несколько крупнейших возмущений лунной долготы (вклад в разницу ее истинной эклиптической долготы относительно средней долготы). В терминах дифференциальных аргументов их можно выразить следующим образом, с округлением коэффициентов до ближайшей секунды дуги ("):

Уравнение центра

См. Также: Уравнение центра.

• Уравнение центра Луны, или эллиптическое неравенство, было известно, по крайней мере в приближении, древним, начиная с вавилонян и Гиппарха. Более поздние данные свидетельствуют о том, что они соответствуют приблизительному применению закона Кеплера о равных площадях на эллиптической орбите и представляют собой ускорение Луны по мере того, как ее расстояние от Земли уменьшается по мере ее движения к перигею, и затем его замедление замедляется по мере увеличения расстояния от Земли по мере продвижения к апогею. Влияние на долготу Луны можно аппроксимировать рядом слагаемых, первые три из которых являются $+22639''\sin(l)+769''\sin(2l)+36''\sin(3l)$.

Выселение

См. Также: Эвекция

• Выброс (или его приближение) был известен Птолемею, но его название и знание его причины датируются 17 веком. Его влияние на долготу Луны имеет странный период, составляющий около 31,8 дней. Это можно представить по-разному, например, как результат примерно 6-месячной либрации в положении перигея с сопровождающей 6-месячной пульсацией размера эксцентриситета орбиты Луны. Его основной термин $+4586''\sin(2D-l)$.

Вариант

Смотрите также: Вариация (астрономия)

• Вариация, открытая Тихо Браге, представляет собой ускорение Луны по мере приближения к новолунию и полнолунию и замедление по мере приближения к первой и последней четверти. Ее гравитационное объяснение с количественной оценкой впервые дал Ньютон. Его основной термин $+2370''\sin(2D)$.

уравнение

• Годовое уравнение, также открытое Браге, было качественно объяснено Ньютоном в терминах того, что орбита Луны становится немного расширенной по размеру и более продолжительной по периоду, когда в начале января Земля находится в перигелии, ближайшем к Солнцу, а орбита Солнца возмущающий эффект является самым сильным, а затем слегка сокращается по размеру и короче по периоду, когда Солнце находится наиболее далеко в начале июля, так что его возмущающий эффект становится слабее: современное значение главного члена, обусловленного этим эффектом, равно $-668''\sin(l')$.

неравенство

• Параллактическое неравенство, впервые обнаруженное Ньютоном, делает вариант Браге немного асимметричным из-за конечного расстояния и ненулевого параллакса Солнца. Его эффект заключается в том, что Луна немного отстает в первой четверти и немного впереди в последней четверти. Его основной термин $-125''\sin(D)$.

Приведение к эклиптике

• Приведение к эклиптике представляет собой геометрический эффект выражения движения Луны через долготу в плоскости эклиптики, хотя на самом деле ее движение происходит в плоскости, наклоненной примерно на 5 градусов. Его основной термин $-412''\sin(2F)$.

Аналитики середины XVIII века выражали возмущения положения Луны по долготе, используя около 25-30 тригонометрических терминов. Однако работы в девятнадцатом и двадцатом веках привели к совершенно разным формулировкам теории, поэтому эти термины больше не актуальны. Число членов, необходимых для выражения положения Луны с точностью, к которой стремились в начале двадцатого века, составляло более 1400; а количество членов, необходимых для имитации точности современных численных интеграций, основанных на наблюдениях с помощью лазерной локации, исчисляется десятками тысяч: нет предела увеличению количества необходимых членов по мере увеличения требований к точности.

Современные разработки

Луны

Установка лазерной локации в Центре космических полетов Годдарда

После Второй мировой войны и особенно с 1960-х годов теория Луны получила дальнейшее развитие несколько иным путем. Это стимулировалось двумя способами: с одной стороны, использованием автоматических цифровых вычислений, а с другой стороны, современными типами данных наблюдений со значительно возросшей точностью и точностью.

Уоллес Джон Эккерт , ученик Эрнеста Уильяма Брауна и сотрудник IBM , использовал экспериментальные цифровые компьютеры, разработанные там после Второй мировой войны, для вычисления астрономических эфемерид. Один из проектов заключался в том, чтобы поместить в машину лунную теорию Брауна и напрямую оценить выражения. Другой проект был чем-то совершенно новым: численное интегрирование уравнений движения Солнца и четырех главных планет. Это стало возможным только после того, как стали доступны электронные цифровые компьютеры. В конечном итоге это привело к созданию серии «Эфемериды развития лаборатории реактивного движения» .

Тем временем теория Брауна была улучшена за счет улучшения констант, введения эфемеридного времени и удаления некоторых связанных с этим эмпирических поправок. Это привело к созданию улучшенных лунных эфемерид (ILE). который, с некоторыми небольшими последовательными улучшениями, использовался в астрономических альманахах с 1960 по 1983 год. и позволил осуществить высадку на Луну .

Наиболее значительным усовершенствованием наблюдений за положением Луны стали измерения лунной лазерной локации , полученные с использованием наземных лазеров и специальных ретрорефлекторов, размещенных на поверхности Луны. Время прохождения импульса лазерного света до одного из ретрорефлекторов и обратно дает представление о расстоянии до Луны в этот момент. Первый из пяти ретрорефлекторов , действующих сегодня, был доставлен на Луну на космическом корабле «Аполлон-11» в июле 1969 года и размещен в подходящем месте на поверхности Луны Баззом Олдрином . Точность дальности была еще больше увеличена благодаря операции по лунной лазерной локации обсерватории Апач-Пойнт , созданной в 2005 году.

Численное интегрирование, теория относительности, приливы, либрации

Лунная теория, разработанная численно с высокой точностью с использованием этих современных мер, основана на более широком диапазоне соображений, чем классические теории: она учитывает не только гравитационные силы (с релятивистскими поправками), но также многие приливные и геофизические эффекты и значительно расширенная теория лунной либрации . Как и многие другие научные области, эта в настоящее время развивается и основывается на работе больших групп и институтов. Одну из ведущих ролей в этих разработках сыграла Лаборатория реактивного движения (JPL) Калифорнийского технологического института ; и имена, особенно связанные с переходом с начала 1970-х годов и далее от классических теорий Луны и эфемерид к современному состоянию науки, включают имена Дж. Деррала Малхолланда и Дж. Г. Уильямса, а также связанные с этим разработки (планетарных) эфемерид Солнечной системы. Э. Майлз Стэндиш.

С 1970-х годов JPL выпускает серию численно интегрированных эфемерид развития (с номером DExxx), включая лунные эфемериды (LExxx). Планетарные и лунные эфемериды DE200/LE200 использовались в эфемеридах официального Астрономического Альманаха за 1984–2002 гг., а эфемериды DE405/LE405 с еще большей точностью и точностью использовались начиная с выпуска за 2003 г. Текущие эфемериды — DE440.

Аналитические разработки

Параллельно с этими разработками в последние годы был разработан новый класс аналитической теории Луны, в частности, « Эфемериды Лунного Парижа». Жан Шапрон и Мишель Шапрон-Тузе из Бюро долгот . Используя компьютерную алгебру, аналитические разработки пошли дальше, чем раньше могли сделать классические аналитики, работающие вручную. Кроме того, некоторые из этих новых аналитических теорий (например, ELP) были адаптированы к числовым эфемеридам, ранее разработанным в JPL, как упоминалось выше. Основные цели этих недавних аналитических теорий, в отличие от целей классических теорий прошлых столетий, не заключались в получении улучшенных позиционных данных на текущие даты; скорее, их цели включали изучение дальнейших аспектов движения, таких как долговременные свойства, которые, возможно, не так легко очевидны из самих современных численных теорий.

Библиография

• «AE 1871»: «Морской альманах и астрономические эфемериды» за 1871 год (Лондон, 1867 г.).
• Э. У. Браун (1896). Вводный трактат по теории Луны , Издательство Кембриджского университета.
• Э. У. Браун. «Теория движения Луны» , Мемуары Королевского астрономического общества , 53 (1897), 39–116.
• Э. У. Браун. «Теория движения Луны» , Мемуары Королевского астрономического общества , 53 (1899), 163–202.
• Э. У. Браун. «Теория движения Луны» , Мемуары Королевского астрономического общества , 54 (1900), 1–63.
• Э. У. Браун. «О проверке закона Ньютона» , Ежемесячные заметки Королевского астрономического общества 63 (1903), 396–397.
• Э. У. Браун. «Теория движения Луны» , Мемуары Королевского астрономического общества , 57 (1905), 51–145.
• Э. У. Браун. «Теория движения Луны» , Мемуары Королевского астрономического общества , 59 (1908), 1–103.
• Э. У. Браун (1919). Таблицы движения Луны , Нью-Хейвен.
• М. Шапрон-Тузе и Ж. Шапрон. «Лунная эфемерида ELP-2000» , Astronomy & Astrophysicals 124 (1983), 50–62.
• М. Шапрон-Тузе и Дж. Шапрон: «ELP2000-85: полуаналитические лунные эфемериды, адекватные историческим временам» , Astronomy & Astrophysicals 190 (1988), 342–352.
• М. Шапрон-Тузе и Ж. Шапрон, Аналитические эфемериды Луны в 20 веке (Парижская обсерватория, 2002).
• Дж. Чапронт; М. Шапрон-Тузе; Г Франку. «Новое определение параметров лунной орбиты, постоянной прецессии и приливного ускорения на основе измерений LLR» , Astronomy & Astrophysicals 387 (2002), 700–709.
• Дж. Шапрон и Дж. Франку. «Возврат к теории Луны ELP. Введение новых планетарных возмущений» , Astronomy & Astrophysicals 404 (2003), 735–742.
• И.Б. Коэн и Энн Уитмен (1999). Исаак Ньютон: «Начала», новый перевод , University of California Press. (Библиографические сведения, но без текста, см. внешнюю ссылку .)
• Джо Дики; ПЛ Бендер; Дж. Э. Фаллер; и другие. «Лунная лазерная локация: продолжающееся наследие программы Аполлон» , Science 265 (1994), стр. 482–490.
• Дж. Л. Дрейер (1906). История астрономии от Фалеса до Кеплера , издательство Кембриджского университета (позже переиздано под измененным названием «История планетных систем от Фалеса до Кеплера»).
• У. Дж. Эккерт и др. Улучшенные лунные эфемериды 1952–1959: совместное дополнение к американским эфемеридам и (британскому) морскому альманаху (Типография правительства США, 1954).
• Дж. Эппинг и Дж. Н. Страссмайер. «О расшифровке халдейских астрономических таблиц», Голоса Марии Лаах , т. 21 (1881), стр. 277–292.
• «ESAE 1961»: «Пояснительное дополнение к астрономическим эфемеридам, американским эфемеридам и навигационному альманаху» («подготовлено совместно Управлением морских альманахов Соединенного Королевства и Соединенных Штатов Америки»), Лондон (HMSO), 1961.
• К. Гартуэйт; Д.Б. Холдридж и Дж.Д. Малхолланд. «Предварительная специальная теория возмущений движения Луны» , Astronomical Journal 75 (1970), 1133.
• Х. Годфрей (1885). Элементарный трактат по теории Луны , Лондон, (4-е изд.).
• Эндрю Мотт (1729а) (переводчик). «Математические принципы естественной философии сэра Исаака Ньютона, переведенные на английский язык», том I, содержащий книгу 1 .
• Эндрю Мотт (1729b) (переводчик). «Математические принципы естественной философии сэра Исаака Ньютона, переведенные на английский язык», том II, содержащий книги 2 и 3 (с указателем, приложением, содержащим дополнительные (ньютоновские) доказательства, и «Законы движения Луны согласно гравитации». , Джон Мачин).
• Джей Ди Малхолланд и Пи Джей Шелус. «Улучшение численных лунных эфемерид с помощью данных лазерной локации» , Moon 8 (1973), 532.
• О Нойгебауэр (1975). История древней математической астрономии (в 3 томах), Нью-Йорк (Спрингер).
• XX Ньюхолл; Э.М. Стэндиш; Дж. Дж. Уильямс. «DE102: Численно интегрированные эфемериды Луны и планет, охватывающие сорок четыре века» , Astronomy and Astrophysicals 125 (1983), 150.
• Военно-морская обсерватория США (2009 г.). «История астрономического альманаха». Архивировано 5 марта 2009 г. в Wayback Machine .
• Дж. Г. Уильямс и др. «Принятие решений на основе данных лунной лазерной локации», Бюллетень Американского астрономического общества (1972), 4Q, 267.
• Дж. Г. Уильямс; С.Г. Турышев; и Д. Х. Боггс. «Прогресс в испытаниях релятивистской гравитации на лунной лазерной локации» , Physical Review Letters , 93 (2004), 261101.

Внешние ссылки

• Цитаты, связанные с теорией Луны , в Wikiquote