Радиальная скорость

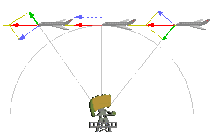
Самолет, пролетающий мимо радиолокационной станции: вектор скорости самолета (красный) представляет собой сумму радиальной скорости (зеленый) и тангенциальной скорости (синий).

Радиальная скорость или скорость прямой видимости цели относительно наблюдателя — это изменения векторного скорость смещения между двумя точками. Он формулируется как векторная проекция цели-наблюдателя относительной скорости на относительное направление или линию прямой видимости (LOS), соединяющую две точки.

Радиальная скорость или скорость дальности — это временная скорость расстояния между двумя или дальности точками. Это со знаком скалярная величина , сформулированная как скалярная проекция вектора относительной скорости на направление прямой видимости. Эквивалентно, радиальная скорость равна норме радиальной скорости по модулю знака. ^[а]

В астрономии за точку обычно принимается наблюдатель на Земле, поэтому лучевая скорость тогда обозначает скорость, с которой объект удаляется от Земли (или приближается к ней, при отрицательной лучевой скорости).

Формулировка

Учитывая дифференцируемый вектор ${\vec {r}}\in \mathbb {R} ^{3}$ определение мгновенного относительного положения цели относительно наблюдателя.

Пусть мгновенная относительная скорость цели относительно наблюдателя равна

{\vec {v}}={\frac {d{\vec {r}}}{dt}}\in \mathbb {R} ^{3}

( 1 )

Величина вектора положения ${\vec {r}}$ определяется как внутренний продукт

r=\|{\vec {r}}\|=\langle {\vec {r}},{\vec {r}}\rangle ^{1/2}

( 2 )

Скорость изменения величины — это производная по времени величины ( нормы ) ${\vec {r}}$ , выраженный как

{\dot {r}}={\frac {dr}{dt}}

( 3 )

Подставив ( 2 ) в ( 3 )

{\dot {r}}={\frac {d\langle {\vec {r}},{\vec {r}}\rangle ^{1/2}}{dt}}

Вычисление производной правой части по цепному правилу

{\dot {r}}={\frac {1}{2}}{\frac {d\langle {\vec {r}},{\vec {r}}\rangle }{dt}}{\frac {1}{r}}

{\dot {r}}={\frac {1}{2}}{\frac {\langle {\frac {d{\vec {r}}}{dt}},{\vec {r}}\rangle +\langle {\vec {r}},{\frac {d{\vec {r}}}{dt}}\rangle }{r}}

используя ( 1 ), выражение становится

{\dot {r}}={\frac {1}{2}}{\frac {\langle {\vec {v}},{\vec {r}}\rangle +\langle {\vec {r}},{\vec {v}}\rangle }{r}}

По взаимности, ^[1] $\langle {\vec {v}},{\vec {r}}\rangle =\langle {\vec {r}},{\vec {v}}\rangle$ .Определение единичного вектора относительного положения ${\hat {r}}={\vec {r}}/{r}$ (или направление LOS), скорость дальности просто выражается как

{\dot {r}}={\frac {\langle {\vec {r}},{\vec {v}}\rangle }{r}}=\langle {\hat {r}},{\vec {v}}\rangle

т. е. проекция вектора относительной скорости на направление прямой видимости.

Дальнейшее определение направления скорости ${\hat {v}}={\vec {v}}/{v}$ , с относительная скорость $v=\|{\vec {v}}\|$ , у нас есть:

{\dot {r}}=v\langle {\hat {r}},{\hat {v}}\rangle =v\langle {\hat {r}},{\hat {v}}\rangle

где внутренний продукт равен +1 или -1 для параллельных и антипараллельных векторов соответственно.

Сингулярность существует для совпадающей цели наблюдателя, т. е. $r=0$ ; в этом случае скорость диапазона не определена.

Приложения в астрономии

В астрономии лучевую скорость часто измеряют в первом порядке приближения с помощью доплеровской спектроскопии . Величину, полученную этим методом, можно назвать барицентрической мерой лучевой скорости или спектроскопической лучевой скоростью. ^[2] Однако из-за релятивистских и космологических эффектов на больших расстояниях, которые обычно проходит свет от астрономического объекта, чтобы достичь наблюдателя, эту меру невозможно точно преобразовать в геометрическую лучевую скорость без дополнительных предположений об объекте и пространстве между ним и наблюдателем. . ^[3] Напротив, астрометрическая лучевая скорость определяется астрометрическими наблюдениями (например, вековым изменением годового параллакса ). ^[3]^[4]^[5]

Спектроскопическая лучевая скорость

Свет от объекта со значительной относительной радиальной скоростью при излучении будет подвержен эффекту Доплера , поэтому частота света уменьшается для удаляющихся объектов ( красное смещение ) и увеличивается для приближающихся объектов ( синее смещение ).

Лучевую скорость звезды или других светящихся далеких объектов можно точно измерить, взяв спектр высокого разрешения и сравнив измеренные длины волн известных спектральных линий с длинами волн, полученными в результате лабораторных измерений. Положительная радиальная скорость указывает на то, что расстояние между объектами увеличивается или увеличивалось; Отрицательная лучевая скорость указывает на то, что расстояние между источником и наблюдателем уменьшается или уменьшалось.

В 1868 году Уильям Хаггинс рискнул оценить лучевую скорость Сириуса относительно Солнца, основываясь на наблюдаемом красном смещении света звезды. ^[6]

Диаграмма, показывающая, как орбита экзопланеты меняет положение и скорость звезды, когда они вращаются вокруг общего центра масс.

У многих двойных звезд орбитальное движение обычно вызывает изменения лучевой скорости на несколько километров в секунду (км/с). Поскольку спектры этих звезд изменяются из-за эффекта Доплера, их называют спектрально-двойными . Лучевую скорость можно использовать для оценки соотношения масс звезд и некоторых элементов орбит , таких как эксцентриситет и большая полуось . Тот же метод также использовался для обнаружения планет вокруг звезд: измерение движения определяет период обращения планеты, а полученная в результате амплитуда лучевой скорости позволяет рассчитать нижнюю границу массы планеты с использованием функции двойной массы . Одни только методы лучевых скоростей могут выявить только нижнюю границу, поскольку большая планета, вращающаяся под очень большим углом к лучу зрения, будет возмущать свою звезду в радиальном направлении так же, как гораздо меньшая планета с плоскостью орбиты на луче зрения. Было высказано предположение, что планеты с высокими эксцентриситетами, рассчитанными этим методом, на самом деле могут представлять собой двухпланетные системы с круговой или околокруговой резонансной орбитой. ^[7]^[8]

Обнаружение экзопланет

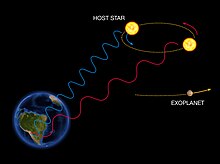
Метод лучевых скоростей для обнаружения экзопланет основан на обнаружении изменений скорости центральной звезды из-за изменения направления гравитационного притяжения (невидимой) экзопланеты, когда она вращается вокруг звезды. Когда звезда движется к нам, ее спектр смещается в голубую сторону, а при удалении от нас — в красную. Регулярно глядя на спектр звезды и, таким образом, измеряя ее скорость, можно определить, движется ли она периодически из-за влияния экзопланеты-компаньона.

Сокращение данных

С инструментальной точки зрения скорости измеряются относительно движения телескопа. Таким образом, важным первым шагом сокращения данных является удаление вкладов

вокруг эллиптическое движение Земли Солнца со скоростью примерно ± 30 км/с,
ежемесячное вращение Земли вокруг центра тяжести системы Земля-Луна со скоростью ±13 м/с, ^[9]
суточное вращение телескопа с земной корой вокруг оси Земли, составляющее на экваторе до ±460 м/с и пропорциональное косинусу географической широты телескопа,
Земли небольшие вклады от движения полюсов на уровне мм/с,
вклады 230 км/с от движения вокруг Галактического Центра и связанных с ним собственных движений. ^[10]
в случае спектроскопических измерений поправки порядка ±20 см/с по аберрации . ^[11]
Грех и вырождение — это воздействие, вызванное нахождением вне плоскости движения.

См. также

Собственное движение - мера наблюдаемых изменений видимого местоположения звезд.
Своеобразная скорость - скорость объекта относительно системы покоя.
Относительная скорость - скорость объекта или наблюдателя в системе отсчета покоя другого объекта или наблюдателя.
Космическая скорость (астрономия) - Исследование движения звезд
Бистатическая дальность действия
Эффект Доплера
Внутренний продукт
Определение орбиты
пространство ЛП

Примечания

^ Норма, неотрицательное число, умножается на -1, если скорость (красная стрелка на рисунке) и относительное положение образуют тупой угол или если относительная скорость (зеленая стрелка) и относительное положение антипараллельны.

Ссылки

^ Хоффман, Кеннет М.; Кунцель, Рэй (1971). Линейная алгебра (Второе изд.). Prentice-Hall Inc. с. 271 . ISBN 0135367972 .
^ Резолюция C1 об определении спектроскопической «барицентрической меры лучевой скорости» . Специальный выпуск: Предварительная программа XXV ГА в Сиднее, 13–26 июля 2003 г., Информационный бюллетень № 91. Страница 50. Секретариат МАС. Июль 2002 г. https://www.iau.org/static/publications/IB91.pdf .
^ Перейти обратно: ^а ^б Линдегрен, Леннарт; Дравинс, Дайнис (апрель 2003 г.). «Основное определение «лучевой скорости» » (PDF) . Астрономия и астрофизика . 401 (3): 1185–1201. arXiv : astro-ph/0302522 . Бибкод : 2003A&A...401.1185L . дои : 10.1051/0004-6361:20030181 . S2CID 16012160 . Проверено 4 февраля 2017 г.
^ Дравинс, Дайнис; Линдегрен, Леннарт; Мэдсен, Сорен (1999). «Астрометрические лучевые скорости. I. Неспектроскопические методы измерения лучевой скорости звезд». Астрон. Астрофизика . 348 : 1040–1051. arXiv : astro-ph/9907145 . Бибкод : 1999A&A...348.1040D .
^ Резолюция C 2 об определении «астрометрической лучевой скорости» . Специальный выпуск: Предварительная программа XXV ГА в Сиднее, 13–26 июля 2003 г., Информационный бюллетень № 91. Страница 51. Секретариат МАС. Июль 2002 г. https://www.iau.org/static/publications/IB91.pdf .
^ Хаггинс, В. (1868). «Дальнейшие наблюдения за спектрами некоторых звезд и туманностей с попыткой определить, движутся ли эти тела к Земле или от нее, а также наблюдения за спектрами Солнца и кометы II». Философские труды Лондонского королевского общества . 158 : 529–564. Бибкод : 1868RSPT..158..529H . дои : 10.1098/rstl.1868.0022 .
^ Англада-Эскуде, Гиллем; Лопес-Моралес, «Мерседес»; Чемберс, Джон Э. (2010). «Как эксцентричные орбитальные решения могут скрыть планетные системы на резонансных орбитах 2: 1». Письма астрофизического журнала . 709 (1): 168–78. arXiv : 0809.1275 . Бибкод : 2010ApJ...709..168A . дои : 10.1088/0004-637X/709/1/168 . S2CID 2756148 .
^ Кюрстер, Мартин; Трифонов, Трифон; Реферт, Сабина; Костогрыз, Надежда М.; Родер, Флориан (2015). «Распутывание резонансных орбит лучевой скорости 2: 1 от эксцентрических и тематическое исследование для HD 27894». Астрон. Астрофизика . 577 : А103. arXiv : 1503.07769 . Бибкод : 2015A&A...577A.103K . дои : 10.1051/0004-6361/201525872 . S2CID 73533931 .
^ Феррас-Мелло, С.; Мищенко Т.А. (2005). «Внесолнечные планетные системы». Хаос и стабильность в планетных системах . Конспект лекций по физике. Том. 683. стр. 219–271. Бибкод : 2005LNP...683..219F . дои : 10.1007/10978337_4 . ISBN 978-3-540-28208-2 . {{cite book}}: |journal= игнорируется ( помогите )
^ Рид, MJ; Дама, ТМ (2016). «О скорости вращения Млечного Пути, определенной по излучению HI» . Астрофизический журнал . 832 (2): 159. arXiv : 1608.03886 . Бибкод : 2016ApJ...832..159R . дои : 10.3847/0004-637X/832/2/159 . S2CID 119219962 .
^ Стампфф, П. (1985). «Строгое рассмотрение гелиоцентрического движения звезд». Астрон. Астрофизика . 144 (1): 232. Бибкод : 1985A&A...144..232S .

Дальнейшее чтение

Хоффман, Кеннет М.; Кунцель, Рэй (1971), Линейная алгебра (второе изд.), Prentice-Hall Inc., ISBN 0135367972
Рензе, Джон; Стовер, Кристофер; и Вайсштейн, Эрик В. «Внутренний продукт». Из MathWorld — веб-ресурса Wolfram. http://mathworld.wolfram.com/InnerProduct.html

Внешние ссылки

Уравнение лучевой скорости при поиске экзопланет (доплеровская спектроскопия или метод воббла)

[1] Норма, неотрицательное число, умножается на -1, если скорость (красная стрелка на рисунке) и относительное положение образуют тупой угол или если относительная скорость (зеленая стрелка) и относительное положение антипараллельны.

[2] Хоффман, Кеннет М.; Кунцель, Рэй (1971). Линейная алгебра (Второе изд.). Prentice-Hall Inc. с. 271 . ISBN 0135367972 .

[IAUInfBull91_c1-3] Резолюция C1 об определении спектроскопической «барицентрической меры лучевой скорости» . Специальный выпуск: Предварительная программа XXV ГА в Сиднее, 13–26 июля 2003 г., Информационный бюллетень № 91. Страница 50. Секретариат МАС. Июль 2002 г. https://www.iau.org/static/publications/IB91.pdf .

[Lindegren2003-4] Перейти обратно: ^а ^б Линдегрен, Леннарт; Дравинс, Дайнис (апрель 2003 г.). «Основное определение «лучевой скорости» » (PDF) . Астрономия и астрофизика . 401 (3): 1185–1201. arXiv : astro-ph/0302522 . Бибкод : 2003A&A...401.1185L . дои : 10.1051/0004-6361:20030181 . S2CID 16012160 . Проверено 4 февраля 2017 г.

[5] Дравинс, Дайнис; Линдегрен, Леннарт; Мэдсен, Сорен (1999). «Астрометрические лучевые скорости. I. Неспектроскопические методы измерения лучевой скорости звезд». Астрон. Астрофизика . 348 : 1040–1051. arXiv : astro-ph/9907145 . Бибкод : 1999A&A...348.1040D .

[IAUInfBull91_c2-6] Резолюция C 2 об определении «астрометрической лучевой скорости» . Специальный выпуск: Предварительная программа XXV ГА в Сиднее, 13–26 июля 2003 г., Информационный бюллетень № 91. Страница 51. Секретариат МАС. Июль 2002 г. https://www.iau.org/static/publications/IB91.pdf .

[7] Хаггинс, В. (1868). «Дальнейшие наблюдения за спектрами некоторых звезд и туманностей с попыткой определить, движутся ли эти тела к Земле или от нее, а также наблюдения за спектрами Солнца и кометы II». Философские труды Лондонского королевского общества . 158 : 529–564. Бибкод : 1868RSPT..158..529H . дои : 10.1098/rstl.1868.0022 .

[Anglada-Escude-8] Англада-Эскуде, Гиллем; Лопес-Моралес, «Мерседес»; Чемберс, Джон Э. (2010). «Как эксцентричные орбитальные решения могут скрыть планетные системы на резонансных орбитах 2: 1». Письма астрофизического журнала . 709 (1): 168–78. arXiv : 0809.1275 . Бибкод : 2010ApJ...709..168A . дои : 10.1088/0004-637X/709/1/168 . S2CID 2756148 .

[KursterAA2015-9] Кюрстер, Мартин; Трифонов, Трифон; Реферт, Сабина; Костогрыз, Надежда М.; Родер, Флориан (2015). «Распутывание резонансных орбит лучевой скорости 2: 1 от эксцентрических и тематическое исследование для HD 27894». Астрон. Астрофизика . 577 : А103. arXiv : 1503.07769 . Бибкод : 2015A&A...577A.103K . дои : 10.1051/0004-6361/201525872 . S2CID 73533931 .

[FMelloLNP683-10] Феррас-Мелло, С.; Мищенко Т.А. (2005). «Внесолнечные планетные системы». Хаос и стабильность в планетных системах . Конспект лекций по физике. Том. 683. стр. 219–271. Бибкод : 2005LNP...683..219F . дои : 10.1007/10978337_4 . ISBN 978-3-540-28208-2 . {{cite book}}: |journal= игнорируется ( помогите )

[Reiadarxiv1608-11] Рид, MJ; Дама, ТМ (2016). «О скорости вращения Млечного Пути, определенной по излучению HI» . Астрофизический журнал . 832 (2): 159. arXiv : 1608.03886 . Бибкод : 2016ApJ...832..159R . дои : 10.3847/0004-637X/832/2/159 . S2CID 119219962 .

[StumpffAA-12] Стампфф, П. (1985). «Строгое рассмотрение гелиоцентрического движения звезд». Астрон. Астрофизика . 144 (1): 232. Бибкод : 1985A&A...144..232S .

[а]

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]