Звездный параллакс

Для более широкого освещения этой темы см. Параллакс в астрономии .

Звездный параллакс является основой парсека , который представляет собой расстояние от Солнца до астрономического объекта , угол параллакса которого составляет одну угловую секунду . (1 а.е. и 1 парсек не в масштабе, 1 парсек = ~ 206265 а.е.)

Звездный параллакс — это видимое смещение положения ( параллакса ) любой близлежащей звезды (или другого объекта) на фоне далеких звезд. В более широком смысле, это метод определения расстояния до звезды посредством тригонометрии, метод звездного параллакса . Созданный разным орбитальным положением Земли , чрезвычайно небольшой наблюдаемый сдвиг является наибольшим через интервалы времени около шести месяцев, когда Земля достигает противоположных сторон Солнца на своей орбите, что дает базовое расстояние между наблюдениями около двух астрономических единиц . Сам параллакс астрономическую считается половиной этого максимума, что примерно эквивалентно наблюдательному сдвигу, который может произойти из-за разного положения Земли и Солнца, базовой линии в одну единицу (а.е.).

Звездный параллакс настолько трудно обнаружить, что его существование было предметом многочисленных споров в астрономии на протяжении сотен лет. Томас Хендерсон , Фридрих Георг Вильгельм фон Струве и Фридрих Бессель провели первые успешные измерения параллакса в 1832–1838 годах для звезд Альфа Центавра , Вега и 61 Лебедя .

Метод параллакса

Принцип

В течение года отмечается положение звезды S по отношению к другим звездам в ее видимом окружении:

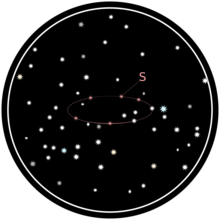
Звезды, которые, казалось, не двигались относительно друг друга, используются в качестве ориентиров для определения пути С.

Наблюдаемый путь представляет собой эллипс: проекцию орбиты Земли вокруг Солнца через точку S на далекий фон неподвижных звезд. Чем дальше S удален от оси орбиты Земли, тем больше эксцентриситет пути S. Центр эллипса соответствует точке, где S можно было бы увидеть с Солнца:

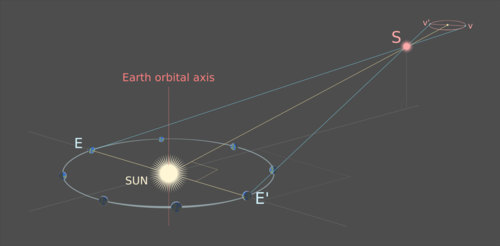
Плоскость орбиты Земли находится под углом к ​​линии, идущей от Солнца через S. Вершины v и v' эллиптической проекции пути S являются проекциями положений Земли E и E ′ так, что линия EE ′ пересекает линия Солнце-S под прямым углом; треугольник, созданный точками E, E ′ и S, является равнобедренным треугольником с линией Sun-S в качестве оси симметрии.

Любые звезды, которые не перемещались между наблюдениями, в целях точности измерений находятся бесконечно далеко. Это означает, что расстояние движения Земли по сравнению с расстоянием до этих бесконечно далеких звезд в пределах точности измерения равно 0. Таким образом, линия обзора от первого положения Земли E до вершины v будет по существу той же самой. как линия взгляда от второго положения Земли E ′ до той же вершины v и, следовательно, будет проходить параллельно ей - невозможно убедительно изобразить на изображении ограниченного размера:

Поскольку прямая E' - v ' является трансверсалью в той же (приблизительно евклидовой) плоскости, что и параллельные прямые Ev и E' - v, то соответствующие углы пересечения этих параллельных прямых с этой трансверсалью равны: угол θ между лучи зрения Ev и E' - v ' равны углу θ между E' - v и E' - v ' , который представляет собой угол θ между наблюдаемыми положениями S по отношению к ее явно неподвижному звездному окружению.

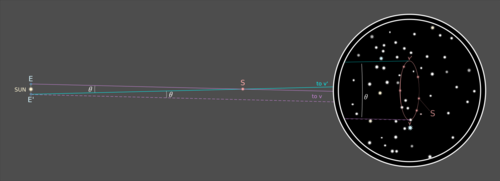
Расстояние d от Солнца до S теперь следует из простой тригонометрии:

  tan(⁠1/2⁠θ) = E-Sun / d, 

так что d = E-Sun/tan( ⁠ 1/2 θ), где E ⁠ - Солнце равно 1 а.е.

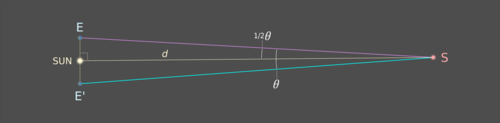
Чем дальше объект, тем меньше его параллакс.

Меры звездного параллакса даются в крошечных единицах угловых секунд или даже в тысячных долях угловых секунд (миллиугловых секундах). Единица расстояния парсек определяется как длина катета прямоугольного треугольника , примыкающего к углу в одну угловую секунду в одной вершине , где длина другого катета составляет 1 а.е. Поскольку звездные параллаксы и расстояния включают в себя такие тонкие прямоугольные треугольники , можно использовать удобное тригонометрическое приближение для преобразования параллаксов (в угловых секундах) в расстояние (в парсеках). Приблизительное расстояние — это просто величина, обратная параллаксу: $d{\text{ (pc)}}\approx 1/p{\text{ (arcsec)}}.$ Например, Проксима Центавра (ближайшая к Земле звезда, кроме Солнца), параллакс которой равен 0,7685, находится на расстоянии 1/0,7685 парсека = 1,301 парсека (4,24 светового дня).

Варианты

Звездный параллакс чаще всего измеряется с использованием годового параллакса , определяемого как разница в положении звезды, если смотреть с Земли и Солнца, то есть угол, образуемый звездой средним радиусом орбиты Земли вокруг Солнца. Парсек угловой (3,26 светового года ) определяется как расстояние, на котором годовой параллакс равен 1 секунде . Годовой параллакс обычно измеряется путем наблюдения за положением звезды в разное время года по мере движения Земли по своей орбите.

Углы, участвующие в этих расчетах, очень малы и поэтому их трудно измерить. Ближайшая к Солнцу звезда (а также звезда с самым большим параллаксом), Проксима Центавра , имеет параллакс 0,7685 ± 0,0002 угловой секунды. Этот угол примерно равен углу объекта диаметром 2 сантиметра, расположенного на расстоянии 5,3 километра.

Вывод

Для прямоугольного треугольника ,

$\tan p={\frac {1\,{\text{au}}}{d}},$

где $p$ — параллакс, 1 а.е. (149 600 000 км) — примерно среднее расстояние от Солнца до Земли, а $d$ это расстояние до звезды. Используя приближения малого угла (действительны, когда угол мал по сравнению с 1 радианом ),

$\tan x\approx x{\text{ radians}}=x\cdot {\frac {180}{\pi }}{\text{ degrees}}=x\cdot 180\cdot {\frac {3600}{\pi }}{\text{ arcseconds}},$

поэтому параллакс, измеряемый в угловых секундах, равен

$p''\approx {\frac {1{\text{ au}}}{d}}\cdot 180\cdot {\frac {3600}{\pi }}.$

Если параллакс равен 1", то расстояние равно

$d=1{\text{ au}}\cdot 180\cdot {\frac {3600}{\pi }}\approx 206,265{\text{ au}}\approx 3.2616{\text{ ly}}\equiv 1{\text{ parsec}}.$

Это определяет парсек — удобную единицу измерения расстояния с использованием параллакса. Следовательно, расстояние, измеряемое в парсеках, просто $d=1/p$, когда параллакс задан в угловых секундах.

Ошибка

Точные измерения параллакса расстояния имеют связанную с этим ошибку. Эта ошибка измерения угла параллакса не приводит непосредственно к ошибке определения расстояния, за исключением относительно небольших ошибок. Причина этого в том, что ошибка в сторону меньшего угла приводит к большей ошибке в расстоянии, чем ошибка в сторону большего угла.

Однако аппроксимацию ошибки расстояния можно вычислить по формуле

$\delta d=\delta \left({1 \over p}\right)=\left|{\partial \over \partial p}\left({1 \over p}\right)\right|\delta p={\delta p \over p^{2}}$

где d — расстояние, а p — параллакс. Аппроксимация гораздо более точна для ошибок параллакса, которые малы по сравнению с параллаксом, чем для относительно больших ошибок. Для получения значимых результатов в звездной астрономии голландский астроном Флор ван Леувен рекомендует, чтобы ошибка параллакса составляла не более 10% от общего параллакса при вычислении этой оценки ошибки.

История измерений

Ранняя теория и попытки

Гелиометр Доллонда конца 1700-х годов.

Звездный параллакс настолько мал, что его нельзя было наблюдать до 19 века, а его кажущееся отсутствие использовалось как научный аргумент против гелиоцентризма в эпоху раннего Нового времени . , ясно Из геометрии Евклида что этот эффект был бы необнаружим, если бы звезды находились достаточно далеко, но по разным причинам такие гигантские расстояния казались совершенно неправдоподобными: одним из Тихо Браге принципиальных возражений против гелиоцентризма Коперника было то, что для чтобы это было совместимо с отсутствием наблюдаемого звездного параллакса, между орбитой Сатурна и восьмой сферой (неподвижными звездами) должна была бы существовать огромная и маловероятная пустота.

Джеймс Брэдли впервые попытался измерить параллаксы звезд в 1729 году. Движение звезд оказалось слишком незначительным для его телескопа , но вместо этого он обнаружил аберрацию света. и нутацию земной оси и каталогизировали 3222 звезды.

19 и 20 века

Гелиометр Бесселя

Разделенная линза Бамбергского гелиометра (конец XIX века)

Измерение годового параллакса стало первым надежным способом определения расстояний до ближайших звезд. Во втором квартале 19 г. ^й века технический прогресс достиг такого уровня, который обеспечивал достаточную точность и точность измерений звездного параллакса. Джузеппе Каландрелли заметил звездный параллакс в 1805–1806 годах и пришел к значению 4 секунды для звезды Вега, что было сильно завышенной оценкой. Первые успешные измерения параллакса звезд были проведены Томасом Хендерсоном в Кейптауне, Южная Африка , в 1832–1833 годах, где он измерил параллакс одной из ближайших звезд, Альфы Центавра . Между 1835 и 1836 годами астроном Фридрих Георг Вильгельм фон Струве в обсерватории Дерптского университета измерил расстояние до Веги и опубликовал свои результаты в 1837 году. Фридрих Бессель , друг Струве, провел в 1837–1838 годах в Кёнигсбергской обсерватории интенсивную наблюдательную кампанию за звездой 61 Лебедя с использованием гелиометра и опубликовал свои результаты в 1838 году. Хендерсон опубликовал свои результаты в 1839 году, после возвращения из Южной Африки.

Эти три результата, два из которых были измерены с помощью лучших инструментов того времени (большой рефрактор Фраунгофера, используемый Струве, и гелиометр Фраунгофера Бесселя), были первыми в истории, позволившими установить надежную шкалу расстояний до звезд.

Большой гелиометр был установлен в обсерватории Куффнера (в Вене) в 1896 году и использовался для измерения расстояний до других звезд с помощью тригонометрического параллакса. К 1910 году он вычислил 16 расстояний от параллаксов до других звезд из 108, известных науке на тот момент.

Схема гелиометра из Британской энциклопедии 1911 года , которая представляет собой вид на разделенную линзу гелиометра.

Поскольку их было очень трудно измерить, к концу XIX века было получено всего около 60 звездных параллаксов, в основном с помощью нитевого микрометра . Астрографы, использующие астрономические фотографические пластинки, ускорили этот процесс в начале 20 века. Автоматические измерительные машины а более совершенные компьютерные технологии 1960-х годов позволили более эффективно составлять звездные каталоги . В 1980-х годах устройства с зарядовой связью (ПЗС) заменили фотографические пластинки и снизили оптическую погрешность до одной миллисекунды дуги.

Звездный параллакс остается стандартом для калибровки других методов измерения (см. Лестницу космических расстояний ). Точные расчеты расстояния на основе звездного параллакса требуют измерения расстояния от Земли до Солнца, которое теперь известно с исключительной точностью и основано на радиолокационном отражении от поверхностей планет.

Космическая астрометрия

Точное измерение расстояний до звезд Хабблом было расширено в 10 раз дальше Млечного Пути .

В 1989 году спутник Hipparcos был запущен в первую очередь для получения параллаксов и собственных движений близлежащих звезд, что увеличило количество звездных параллаксов, измеренных с точностью до миллисекундной секунды, в тысячу раз. Несмотря на это, Hipparcos способен измерять углы параллакса только для звезд, находящихся на расстоянии до 1600 световых лет , что составляет немногим более одного процента диаметра Галактики Млечный Путь .

Телескоп Хаббл WFC3 теперь имеет точность от 20 до 40 угловых секунд, что позволяет надежно измерять расстояния до 3066 парсеков (10 000 световых лет) для небольшого количества звезд. Это придает большую точность космической лестнице расстояний и улучшает знание расстояний во Вселенной, исходя из размеров орбиты Земли.

По мере увеличения расстояний между двумя точками наблюдения визуальный эффект параллакса также становится более заметным. Космический корабль НАСА « Новые горизонты» выполнил первое измерение межзвездного параллакса 22 апреля 2020 года, сделав изображения Проксимы Центавра и Вольфа 359 совместно с наземными обсерваториями. Относительная близость двух звезд в сочетании с расстоянием космического корабля от Земли в 6,5 миллиардов километров (около 43 а.е.) обеспечили заметный параллакс в угловые минуты, что позволило увидеть параллакс визуально без приборов.

Параллакс Проксимы Центавра, наблюдаемый с корабля «Новые горизонты» и с Земли.

Европейского космического агентства , Ожидается, что миссия Gaia запущенная 19 декабря 2013 года, измерит углы параллакса с точностью до 10 угловых микросекунд для всех умеренно ярких звезд, таким образом составив карту близлежащих звезд (и, возможно, планет) на расстоянии десятков тысяч. световых лет от Земли. В выпуске данных 2 за 2018 год утверждается, что средние ошибки для параллаксов 15-й величины и более ярких звезд составляют 20–40 угловых микросекунд.

Радиоастрометрия

Интерферометрия со очень длинной базой в радиодиапазоне может создавать изображения с угловым разрешением около 1 миллисекунды дуги, и, следовательно, для ярких радиоисточников точность измерений параллакса, выполненных в радиодиапазоне, может легко превысить оптические телескопы, такие как Гайя. Эти измерения, как правило, имеют ограниченную чувствительность, и их необходимо проводить по одному, поэтому работа обычно выполняется только для таких источников, как пульсары и рентгеновские двойные системы, где радиоизлучение сильнее оптического.

См. также

• Видимое место
• ТАУ (космический корабль) (заброшенный проект космической миссии, в котором использовался бы параллакс)

Ссылки

• Хиршфельд, Алан В. (2001). Параллакс: гонка за измерение космоса . Нью-Йорк: WH Freeman. ISBN  0-7167-3711-6 .
• Уиппл, Фред Л. (2007). Земля, Луна и планеты . Читайте книги. ISBN  978-1-4067-6413-0 . .
• Зейлик, Майкл А.; Грегори, Стефан А. (1998). Вводная астрономия и астрофизика (4-е изд.). Издательство Колледжа Сондерса. ISBN  0-03-006228-4 . .

Дальнейшее чтение

• Дайсон, ФРВ (1915). «Измерение расстояний звезд». Обсерватория . 38 : 292. Бибкод : 1915Obs....38..292D .