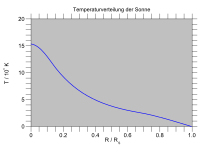
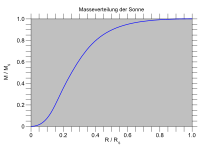
Звездная структура

Модели звездной структуры описывают внутреннюю структуру звезды и подробно делают прогнозы относительно светимости , цвета и будущей эволюции звезды. Разные классы и возрасты звезд имеют разную внутреннюю структуру, отражающую их элементный состав и механизмы транспортировки энергии.

Перенос тепла [ править ]

Информацию о переносе энергии см. в разделе Радиационная передача .

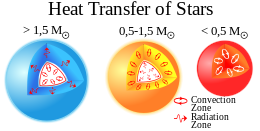
Различные слои звезд переносят тепло и наружу по-разному, в первую очередь конвекцией и радиационной передачей , но теплопроводность важна для белых карликов .

Конвекция является доминирующим способом переноса энергии, когда температурный градиент настолько крут, что данная порция газа внутри звезды будет продолжать подниматься, если она немного поднимется в результате адиабатического процесса . В этом случае поднимающийся пакет является плавучим и продолжает подниматься, если он теплее окружающего газа; если поднимающийся пакет холоднее окружающего газа, он упадет на свою первоначальную высоту. ^[1] В регионах с низким температурным градиентом и достаточно низкой непрозрачностью , позволяющей передавать энергию посредством излучения, излучение является доминирующим способом передачи энергии.

Внутренняя структура звезды главной последовательности зависит от массы звезды.

В звездах с массами 0,3–1,5 солнечных масс ( M _☉ ), включая Солнце, синтез водорода с гелием происходит в основном через протон-протонные цепочки , которые не создают крутого градиента температуры. Таким образом, во внутренней части звезд солнечной массы преобладает излучение. Внешняя часть звезд солнечной массы достаточно холодная, поэтому водород нейтрален и, следовательно, непрозрачен для ультрафиолетовых фотонов, поэтому доминирует конвекция. Следовательно, звезды солнечной массы имеют радиационное ядро с конвективными оболочками во внешней части звезды.

У массивных звезд (более 1,5 M _☉ ) температура ядра выше примерно 1,8×10 ⁷ K , поэтому водорода с гелием синтез происходит в основном через цикл CNO . В цикле CNO скорость генерации энергии масштабируется как температура в 15-й степени, тогда как скорость масштабируется как температура в 4-й степени в протон-протонных цепочках. ^[2] Из-за сильной температурной чувствительности цикла CNO градиент температуры во внутренней части звезды достаточно крутой, чтобы сделать ядро конвективным . Во внешней части звезды градиент температуры меньше, но температура достаточно высока, чтобы водород почти полностью ионизовался , поэтому звезда остается прозрачной для ультрафиолетового излучения. Таким образом, массивные звезды имеют радиационную оболочку.

Звезды главной последовательности с наименьшей массой не имеют зоны излучения; доминирующим механизмом переноса энергии по всей звезде является конвекция. ^[3]

Уравнения звездного строения [ править ]

Профиль температуры на Солнце

Масса внутри заданного радиуса Солнца

Профиль плотности на Солнце

Профиль давления на Солнце

Самая простая и часто используемая модель звездной структуры — это сферически-симметричная квазистатическая модель, которая предполагает, что звезда находится в устойчивом состоянии и что она сферически симметрична . Он содержит четыре основных дифференциальных уравнения первого порядка : два представляют, как материя и давление изменяются в зависимости от радиуса; два представляют, как температура и светимость изменяются в зависимости от радиуса. ^[4]

При формировании уравнений строения звезды (используя предполагаемую сферическую симметрию) учитывается плотность вещества $\rho (r)$ , температура $T(r)$ , полное давление (вещество плюс излучение) $P(r)$ , яркость $l(r)$ , и скорость генерации энергии на единицу массы $\epsilon (r)$ в сферической оболочке толщиной ${\mbox{d}}r$ на расстоянии $r$ от центра звезды. Предполагается, что звезда находится в локальном термодинамическом равновесии (ЛТР), поэтому температура вещества и фотонов одинакова . Хотя LTE строго не соблюдается, поскольку температура, которую данная оболочка «видит» ниже себя, всегда выше, чем температура выше, это приближение обычно превосходно, поскольку средняя длина свободного пробега фотонов $\lambda$ , много меньше длины, на которой температура существенно меняется, т.е. $\lambda \ll T/|\nabla T|$ .

Во-первых, это утверждение гидростатического равновесия : внешняя сила, возникающая из-за градиента давления внутри звезды, точно уравновешивается внутренней силой, вызванной гравитацией . Иногда это называют звездным равновесием.

{{\mbox{d}}P \over {\mbox{d}}r}=-{Gm\rho  \over r^{2}}

,

где $m(r)$ - совокупная масса внутри оболочки при $r$ G . — постоянная гравитационная Совокупная масса увеличивается с радиусом в соответствии с уравнением неразрывности массы :

{{\mbox{d}}m \over {\mbox{d}}r}=4\pi r^{2}\rho .

Интегрируя уравнение неразрывности массы от центра звезды ( $r=0$ ) к радиусу звезды ( $r=R$ ) дает полную массу звезды.

Учитывая энергию, покидающую сферическую оболочку, получаем уравнение энергии:

{{\mbox{d}}l \over {\mbox{d}}r}=4\pi r^{2}\rho (\epsilon -\epsilon _{\nu })

,

где $\epsilon _{\nu }$ — светимость, образующаяся в виде нейтрино (которые обычно покидают звезду, не взаимодействуя с обычным веществом) на единицу массы. За пределами ядра звезды, где происходят ядерные реакции, энергия не генерируется, поэтому светимость постоянна.

Уравнение переноса энергии принимает разные формы в зависимости от способа переноса энергии. Для кондуктивного переноса энергии (подходящего для белого карлика ) уравнение энергии имеет вид

{{\mbox{d}}T \over {\mbox{d}}r}=-{1 \over k}{l \over 4\pi r^{2}},

где k – теплопроводность .

В случае радиационного переноса энергии, подходящего для внутренней части звезды главной последовательности солнечной массы и внешней оболочки массивной звезды главной последовательности,

{{\mbox{d}}T \over {\mbox{d}}r}=-{3\kappa \rho l \over 64\pi r^{2}\sigma T^{3}},

где $\kappa$ это непрозрачность вопроса, $\sigma$ — константа Стефана–Больцмана , а константа Больцмана равна единице.

Случай конвективного переноса энергии не имеет известной строгой математической формулировки и предполагает турбулентность в газе. Конвективный перенос энергии обычно моделируется с использованием теории длины смешивания . При этом газ в звезде рассматривается как содержащий дискретные элементы, которые примерно сохраняют температуру, плотность и давление окружающей среды, но движутся через звезду на характерную длину, называемую длиной смешивания . ^[5] Для одноатомного идеального газа , когда конвекция является адиабатической , что означает, что конвективные пузырьки газа не обмениваются теплом с окружающей средой, теория длины смешивания дает

{{\mbox{d}}T \over {\mbox{d}}r}=\left(1-{1 \over \gamma }\right){T \over P}{{\mbox{d}}P \over {\mbox{d}}r},

где $\gamma =c_{p}/c_{v}$ – показатель адиабаты , отношение теплоемкостей газа. (Для полностью ионизованного идеального газа $\gamma =5/3$ .) Когда конвекция не адиабатическая, истинный градиент температуры не определяется этим уравнением. Например, на Солнце конвекция у основания конвекционной зоны, вблизи ядра, является адиабатической, а у поверхности — нет. Теория длины смешивания содержит два свободных параметра, которые необходимо задать, чтобы модель соответствовала наблюдениям, поэтому это феноменологическая теория, а не строгая математическая формулировка. ^[6]

Также требуются уравнения состояния , связывающие давление, непрозрачность и скорость генерации энергии с другими локальными переменными, подходящими для материала, такими как температура, плотность, химический состав и т. д. Соответствующие уравнения состояния для давления, возможно, должны включать идеальный газ. закон, давление излучения, давление вырожденных электронов и т. д. Непрозрачность не может быть точно выражена одной формулой. Он рассчитан для различных составов при определенных плотностях и температурах и представлен в табличной форме. ^[7] звездных структур Коды (то есть компьютерные программы, вычисляющие переменные модели) либо интерполируют в сетке плотность-температура, чтобы получить необходимую непрозрачность, либо используют аппроксимирующую функцию на основе табличных значений. Аналогичная ситуация имеет место и при точных расчетах уравнения состояния давления. Наконец, скорость генерации ядерной энергии рассчитывается на основе по ядерной физике экспериментов с использованием реакционных сетей для расчета скоростей реакций для каждого отдельного этапа реакции и равновесного содержания каждого изотопа в газе. ^[6]^[8]

В сочетании с набором граничных условий решение этих уравнений полностью описывает поведение звезды. Типичные граничные условия соответствующим образом задают значения наблюдаемых параметров на поверхности ( $r=R$ ) и центр ( $r=0$ ) звезды: $P(R)=0$ , что означает, что давление на поверхности звезды равно нулю; $m(0)=0$ , внутри центра звезды нет массы, как и требуется, если плотность массы остается конечной ; $m(R)=M$ , полная масса звезды равна массе звезды; и $T(R)=T_{eff}$ , температура на поверхности является эффективной температурой звезды.

Хотя в настоящее время модели эволюции звезд описывают основные особенности диаграмм цвет-величина , необходимо внести важные улучшения, чтобы устранить неопределенности, связанные с ограниченными знаниями о явлениях переноса. Самой сложной задачей остается численная обработка турбулентности. ^{[ нужна ссылка ]} Некоторые исследовательские группы разрабатывают упрощенное моделирование турбулентности в 3D-расчетах.

Быстрая эволюция

Вышеупомянутая упрощенная модель неадекватна без модификации в ситуациях, когда изменения состава происходят достаточно быстро. Уравнение гидростатического равновесия, возможно, придется изменить, добавив член радиального ускорения, если радиус звезды меняется очень быстро, например, если звезда радиально пульсирует. ^[9] Кроме того, если ядерное горение нестабильно или ядро звезды быстро разрушается, в уравнение энергии необходимо добавить энтропийный член. ^[10]

См. также [ править ]

Ссылки [ править ]

^ Хансен, Кавалер и Тримбл (2004 , §5.1.1)
^ Хансен, Кавалер и Тримбл (2004 , табл. 1.1)
^ Хансен, Кавалер и Тримбл (2004 , §2.2.1)
^ Это обсуждение следует за обсуждениями, например. например, Зейлик и Грегори (1998 , §16-1–16-2) и Хансен, Кавалер и Тримбл (2004 , §7.1)
^ Хансен, Кавалер и Тримбл (2004 , §5.1)
↑ Перейти обратно: Перейти обратно: ^а ^б Остли, Дейл А. и Кэррол, Брэдли В., Введение в современную звездную астрофизику , Аддисон-Уэсли (2007)
^ Иглесиас, Калифорния; Роджерс, Ф.Дж. (июнь 1996 г.), «Обновленная непрозрачность опала», Astrophysical Journal , 464 : 943–+, Бибкод : 1996ApJ...464..943I , doi : 10.1086/177381 .
^ Раушер, Т.; Хегер, А.; Хоффман, РД; Вусли, С.Э. (сентябрь 2002 г.), «Нуклеосинтез в массивных звездах с улучшенной ядерной и звездной физикой», The Astrophysical Journal , 576 (1): 323–348, arXiv : astro-ph/0112478 , Bibcode : 2002ApJ...576. .323R , дои : 10.1086/341728 .
^ Мойя, А.; Гарридо, Р. (август 2008 г.), «Код колебаний Гранады (GraCo)», Astrophysical and Space Science , 316 (1–4): 129–133, arXiv : 0711.2590 , Bibcode : 2008Ap&SS.316..129M , doi : 10.1007 /s10509-007-9694-2 , S2CID 16150778 .
^ Мюллер, Э. (июль 1986 г.), «Сети ядерных реакций и коды звездной эволюции – связь изменений состава и выделения энергии при взрывном ядерном горении», Astronomy and Astrophysicals , 162 (1–2): 103–108, Bibcode : 1986А&А...162..103М .

Источники [ править ]

Киппенхан, Р.; Вейгерт, А. (1990), Звездная структура и эволюция , Springer-Verlag.
Хансен, Карл Дж.; Кавалер, Стивен Д.; Тримбл, Вирджиния (2004), Stellar Interiors (2-е изд.), Springer, ISBN 0-387-20089-4
Кеннеди, Даллас К.; Бладман, Сидни А. (1997), «Вариационные принципы звездной структуры», Astrophysical Journal , 484 (1): 329–340, arXiv : astro-ph/9610099 , Bibcode : 1997ApJ...484..329K , doi : 10.1086/304333 , S2CID 16835178
Вайс, Ахим; Хиллебрандт, Вольфганг; Томас, Ганс-Кристоф; Риттер, Х. (2004), Принципы звездной структуры Кокса и Джули , Cambridge Scientific Publishers, Bibcode : 2004cgps.book.....W
Зейлик, Майкл А.; Грегори, Стефан А. (1998), Введение в астрономию и астрофизику (4-е изд.), Saunders College Publishing, ISBN 0-03-006228-4

Внешние ссылки [ править ]

код непрозрачности получен в ноябре 2009 г.
Желтый код CESAM , звездная эволюция и структура исходного кода на Фортране
EZ для развития ZAMS Stars — программного обеспечения на FORTRAN 90, созданного на основе кода Eggleton's Stellar Evolution, веб-интерфейс можно найти здесь [1] .
Женевские сетки моделей звездной эволюции (некоторые из них включают перемешивание, вызванное вращением)
База БаСТИ данных треков звездной эволюции

[1] Хансен, Кавалер и Тримбл (2004 , §5.1.1)

[2] Хансен, Кавалер и Тримбл (2004 , табл. 1.1)

[3] Хансен, Кавалер и Тримбл (2004 , §2.2.1)

[4] Это обсуждение следует за обсуждениями, например. например, Зейлик и Грегори (1998 , §16-1–16-2) и Хансен, Кавалер и Тримбл (2004 , §7.1)

[5] Хансен, Кавалер и Тримбл (2004 , §5.1)

[Ostlie-6] Перейти обратно: Перейти обратно: ^а ^б Остли, Дейл А. и Кэррол, Брэдли В., Введение в современную звездную астрофизику , Аддисон-Уэсли (2007)

[Rogers1996-7] Иглесиас, Калифорния; Роджерс, Ф.Дж. (июнь 1996 г.), «Обновленная непрозрачность опала», Astrophysical Journal , 464 : 943–+, Бибкод : 1996ApJ...464..943I , doi : 10.1086/177381 .

[Heger2002-8] Раушер, Т.; Хегер, А.; Хоффман, РД; Вусли, С.Э. (сентябрь 2002 г.), «Нуклеосинтез в массивных звездах с улучшенной ядерной и звездной физикой», The Astrophysical Journal , 576 (1): 323–348, arXiv : astro-ph/0112478 , Bibcode : 2002ApJ...576. .323R , дои : 10.1086/341728 .

[9] Мойя, А.; Гарридо, Р. (август 2008 г.), «Код колебаний Гранады (GraCo)», Astrophysical and Space Science , 316 (1–4): 129–133, arXiv : 0711.2590 , Bibcode : 2008Ap&SS.316..129M , doi : 10.1007 /s10509-007-9694-2 , S2CID 16150778 .

[10] Мюллер, Э. (июль 1986 г.), «Сети ядерных реакций и коды звездной эволюции – связь изменений состава и выделения энергии при взрывном ядерном горении», Astronomy and Astrophysicals , 162 (1–2): 103–108, Bibcode : 1986А&А...162..103М .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]