Сила

Чтобы узнать о других значениях, см. Сила (значения) . «Физическая сила» перенаправляется сюда. Чтобы узнать о других значениях, см. Физическая сила (значения) .

Сила
Силы можно описать как толчок или притяжение объекта. Они могут быть вызваны такими явлениями, как гравитация , магнетизм или чем-то еще, что может вызвать ускорение массы.
Общие символы	${\vec {F}}$, Ф , Ф
И объединились	Ньютон (Н)
Другие подразделения	дина , фунт-сила , паундаль , кип , килопонд
В базовых единицах СИ	кг м · ·с −2
Выводы из другие количества	F = м а
Измерение	${\mathsf {M}}{\mathsf {L}}{\mathsf {T}}^{-2}$

В физике сила — это воздействие, которое может заставить объект изменить свою скорость , т. е. ускориться , что означает изменение скорости или направления, если оно не уравновешено другими силами. Понятие силы делает повседневные представления о толкании или тяге математически точными. Поскольку величина и направление силы важны, сила является векторной величиной. Единицей ( силы в системе СИ является Н) , а сила часто обозначается символом F. ньютон

Сила играет центральную роль в классической механике, фигурируя во всех трёх законах движения Ньютона , которые определяют, что сила, действующая на объект с неизменной массой , равна произведению массы объекта и ускорения , которому он подвергается. Типы сил, часто встречающихся в классической механике, включают упругие , фрикционные , контактные или «нормальные» силы и гравитационные . Вращательная версия силы — это крутящий момент , который вызывает изменения скорости вращения объекта. В расширенном теле каждая часть часто оказывает воздействие на соседние части; Распределением таких сил по телу является внутреннее механическое напряжение . В равновесии эти напряжения не вызывают ускорения тела, поскольку силы уравновешивают друг друга. Если они не находятся в равновесии, они могут вызвать деформацию твердых материалов или течение жидкостей .

В современной физике , которая включает в себя теорию относительности и квантовую механику , законы, управляющие движением, пересматриваются, чтобы полагаться на фундаментальные взаимодействия как на первопричину силы. Однако понимание силы, обеспечиваемое классической механикой, полезно для практических целей.

Разработка концепции

Философы древности использовали концепцию силы при изучении неподвижных и движущихся объектов и простых машин , но такие мыслители, как Аристотель и Архимед, сохраняли фундаментальные ошибки в понимании силы. Отчасти это было связано с неполным пониманием порой неочевидной силы трения и, как следствие, с неадекватным представлением о природе естественного движения. Фундаментальной ошибкой было убеждение, что для поддержания движения даже с постоянной скоростью необходима сила. Большинство прежних заблуждений о движении и силе в конечном итоге были исправлены Галилео Галилеем и сэром Исааком Ньютоном . Благодаря своей математической проницательности Ньютон сформулировал законы движения , которые не совершенствовались более двухсот лет.

К началу 20-го века Эйнштейн разработал теорию относительности , которая правильно предсказала действие сил на объекты с возрастающими импульсами, близкими к скорости света, а также дала представление о силах, создаваемых гравитацией и инерцией . Благодаря современным знаниям в области квантовой механики и технологиям, которые могут ускорять частицы, близкие к скорости света, физика элементарных частиц разработала Стандартную модель для описания сил между частицами, меньшими, чем атомы. Стандартная модель предсказывает, что обменные частицы, называемые калибровочными бозонами, являются фундаментальным средством испускания и поглощения сил. Известны только четыре основных взаимодействия: в порядке убывания силы это: сильное , электромагнитное , слабое и гравитационное . в области физики частиц высоких энергий, Наблюдения сделанные в 1970-х и 1980-х годах, подтвердили, что слабые и электромагнитные взаимодействия являются выражением более фундаментального электрослабого взаимодействия.

Доньютоновские концепции

Смотрите также: Аристотелевская физика и теория импульса.

Аристотель , как известно, описал силу как все, что заставляет объект подвергаться «неестественному движению».

С античных времен концепция силы признавалась неотъемлемой частью функционирования каждой простой машины . Механическое преимущество, обеспечиваемое простой машиной, позволило использовать меньшую силу в обмен на то, что эта сила действует на большем расстоянии и выполняет тот же объем работы . Анализ характеристик сил в конечном итоге завершился работами Архимеда , который особенно прославился разработкой трактовки сил плавучести, присущих жидкостям .

Аристотель провел философское обсуждение понятия силы как неотъемлемой части аристотелевской космологии . По мнению Аристотеля, земная сфера содержала четыре элемента , которые покоятся в разных «естественных местах». Аристотель считал, что неподвижные объекты на Земле, состоящие в основном из элементов земли и воды, находятся на своем естественном месте, когда находятся на земле, и что они остаются такими, если их оставить в покое. Он различал врожденную тенденцию объектов находить свое «естественное место» (например, падение тяжелых тел), приводящую к «естественному движению», и неестественное или вынужденное движение, требующее непрерывного приложения силы. Эта теория, основанная на повседневном опыте движения объектов, например, на постоянном приложении силы, необходимой для поддержания движения тележки, имела концептуальные проблемы с объяснением поведения снарядов , например полета стрел. Лучник заставляет стрелу двигаться в начале полета, а затем она плывет по воздуху, даже если на нее не действует никакая видимая действующая причина. Аристотель знал об этой проблеме и предположил, что воздух, вытесняемый на пути снаряда, доставляет снаряд к цели. Это объяснение требует непрерывной среды, такой как воздух, для поддержания движения.

Хотя физика Аристотеля подвергалась критике еще в VI веке, его недостатки не были исправлены до работы Галилео Галилея 17-го века , который находился под влиянием позднесредневековой идеи о том, что объекты, находящиеся в вынужденном движении, обладают врожденной силой импульса . Галилей провел эксперимент, в котором камни и пушечные ядра катились вниз по склону, чтобы опровергнуть аристотелевскую теорию движения . Он показал, что тела ускоряются под действием силы тяжести до степени, не зависящей от их массы, и утверждал, что объекты сохраняют свою скорость, если на них не действует сила, например трение . Идея Галилея о том, что сила необходима для изменения движения, а не для его поддержания, усовершенствованная Исааком Бекманом , Рене Декартом и Пьером Гассенди , стала ключевым принципом ньютоновской физики.

Ньютона В начале 17 века, до «Начал» , термин «сила» ( лат . vis ) применялся ко многим физическим и нефизическим явлениям, например, к ускорению точки. Произведение точечной массы на квадрат ее скорости назвал vis viva (живая сила) Лейбниц . Современное понятие силы соответствует vis motrix Ньютона (ускоряющая сила).

Механика Ньютона

Основная статья: законы движения Ньютона

Сэр Исаак Ньютон описал движение всех объектов, используя понятия инерции и силы. В 1687 году Ньютон опубликовал свой выдающийся труд «Philosophiæ Naturalis Principia Mathematica» . В этой работе Ньютон изложил три закона движения, которые до сих пор доминируют в описании сил в физике. Точные способы выражения законов Ньютона развивались вместе с новыми математическими подходами.

Первый закон

Основная статья: первый закон Ньютона

Первый закон движения Ньютона гласит, что естественное поведение покоящегося объекта — продолжать находиться в покое, а естественное поведение объекта, движущегося с постоянной скоростью по прямой, — продолжать двигаться с постоянной скоростью по этой прямой линии. Последнее вытекает из первого в силу того принципа, что законы физики одинаковы для всех инерциальных наблюдателей , т. е. всех наблюдателей, не ощущающих себя в движении. Наблюдатель, движущийся вместе с объектом, увидит его покоящимся. Таким образом, его естественным поведением будет оставаться в состоянии покоя по отношению к этому наблюдателю, а это означает, что наблюдатель, который видит, что он движется с постоянной скоростью по прямой линии, увидит, что он продолжает это делать.

Сэр Исаак Ньютон в 1689 году. Его «Начала» представили три закона движения на геометрическом языке, тогда как современная физика использует дифференциальное исчисление и векторы .

Второй закон

Основная статья: второй закон Ньютона

Согласно первому закону, для движения с постоянной скоростью по прямой не нужна причина. Именно изменение движения требует причины, а второй закон Ньютона устанавливает количественную связь между силой и изменением движения. Второй закон Ньютона гласит, что результирующая сила, действующая на объект, равна скорости изменения его импульса со временем . Если масса объекта постоянна, этот закон подразумевает, что ускорение объекта прямо пропорционально чистой силе, действующей на объект, направлено в направлении чистой силы и обратно пропорционально массе объекта .

Современная формулировка второго закона Ньютона представляет собой векторное уравнение:

$$\mathbf {F} ={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}},$$

где $\mathbf {p}$ - это импульс системы, а $\mathbf {F}$ — чистая ( векторная сумма ) сила. Если тело находится в равновесии, результирующая сила по определению равна нулю (тем не менее, уравновешенные силы могут присутствовать). Напротив, второй закон гласит, что если на объект действует несбалансированная сила, это приведет к изменению импульса объекта с течением времени.

В обычных инженерных приложениях масса в системе остается постоянной, что позволяет использовать простую алгебраическую форму для второго закона. По определению импульса,

$$\mathbf {F} ={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}={\frac {\mathrm {d} \left(m\mathbf {v} \right)}{\mathrm {d} t}},$$

где m - масса и $\mathbf {v}$ это скорость . Если второй закон Ньютона применить к системе постоянной массы , m можно вывести за пределы оператора производной. Тогда уравнение становится

$$\mathbf {F} =m{\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}.$$

Путем подстановки определения ускорения алгебраическая версия второго закона Ньютона получается :

$$\mathbf {F} =m\mathbf {a} .$$

Третий закон

Основная статья: Третий закон Ньютона

Всякий раз, когда одно тело оказывает силу на другое, последнее одновременно оказывает на первое равное и противоположное усилие. В векторной форме, если $\mathbf {F} _{1,2}$ - сила тела 1 на тело 2 и $\mathbf {F} _{2,1}$ что тела 2 на теле 1, то

$$\mathbf {F} _{1,2}=-\mathbf {F} _{2,1}.$$

Этот закон иногда называют законом действия-противодействия . $\mathbf {F} _{1,2}$ назвал действие и $-\mathbf {F} _{2,1}$ реакция ​ .

Третий закон Ньютона является результатом применения симметрии к ситуациям, когда силы можно объяснить наличием различных объектов. Третий закон означает, что все силы представляют собой взаимодействия между различными телами. и, таким образом, не существует такой вещи, как однонаправленная сила или сила, действующая только на одно тело.

В системе, состоящей из объекта 1 и объекта 2, результирующая сила, действующая на систему из-за их взаимного взаимодействия, равна нулю:

$$\mathbf {F} _{1,2}+\mathbf {F} _{2,1}=0.$$

В более общем смысле, в замкнутой системе частиц все внутренние силы уравновешены. Частицы могут ускоряться относительно друг друга, но центр масс системы не будет ускоряться. Если на систему действует внешняя сила, она заставит центр масс ускориться пропорционально величине внешней силы, деленной на массу системы.

Объединив второй и третий законы Ньютона, можно показать, что линейный импульс системы сохраняется в любой замкнутой системе . В системе двух частиц, если $\mathbf {p} _{1}$ - импульс объекта 1 и $\mathbf {p} _{2}$ импульс объекта 2, то

$${\frac {\mathrm {d} \mathbf {p} _{1}}{\mathrm {d} t}}+{\frac {\mathrm {d} \mathbf {p} _{2}}{\mathrm {d} t}}=\mathbf {F} _{1,2}+\mathbf {F} _{2,1}=0.$$

Используя аналогичные аргументы, это можно обобщить на систему с произвольным числом частиц. В общем, пока все силы возникают в результате взаимодействия объектов с массой, можно определить систему, в которой чистый импульс никогда не теряется и не приобретается.

Определение слова «сила»

используется второй закон Ньютона . В некоторых учебниках в качестве определения силы Однако для уравнения $\mathbf {F} =m\mathbf {a}$ для постоянной массы $m$ чтобы затем иметь какой-либо прогнозный контент, его необходимо объединить с дополнительной информацией. Более того, вывод о том, что сила присутствует, поскольку тело ускоряется, справедлив только в инерциальной системе отсчета. На вопрос о том, какие аспекты законов Ньютона принять в качестве определений, а какие считать содержащими физическое содержание, давался по-разному. которые в конечном итоге не влияют на то, как теория используется на практике. Среди известных физиков, философов и математиков, которые стремились к более четкому определению понятия силы, — Эрнст Мах и Уолтер Нолл .

Объединение сил

Добавление векторов $v_{1}$ и $v_{2}$ приводит к $v$

Силы действуют в определенном направлении и имеют размеры , зависящие от силы толчка или притяжения. Из-за этих характеристик силы классифицируются как « векторные величины ». Это означает, что силы подчиняются другому набору математических правил, чем физические величины, не имеющие направления (обозначаемые скалярными величинами). необходимо знать как величину, так и направление обеих сил Например, при определении того, что происходит, когда на один и тот же объект действуют две силы, для расчета результата . Если обе эти части информации не известны для каждой силы, ситуация неоднозначна.

Исторически силы впервые количественно исследовались в условиях статического равновесия , когда несколько сил уравновешивали друг друга. Такие эксперименты демонстрируют важнейшие свойства сил как аддитивных векторных величин : они имеют величину и направление. Когда две силы действуют на точечную частицу , результирующая сила, равнодействующая (также называемая чистой силой ), может быть определена, следуя параллелограмма правилу сложения векторов : сложение двух векторов, представленных сторонами параллелограмма, дает эквивалент результирующий вектор, равный по величине и направлению поперечному параллелограмму. Величина равнодействующей варьируется от разности величин двух сил до их суммы в зависимости от угла между их линиями действия.

Схемы свободного тела блока на плоской поверхности и наклонной плоскости . Силы вычисляются и суммируются для определения их величин и чистой силы.

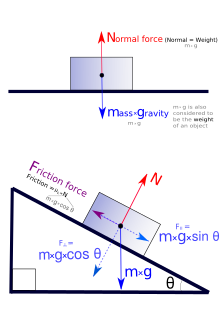
Диаграммы свободного тела можно использовать как удобный способ отслеживать силы, действующие на систему. В идеале эти диаграммы рисуются с сохранением углов и относительных величин векторов сил, чтобы можно было выполнить графическое сложение векторов для определения чистой силы.

Силы не только складываются, но и могут быть разделены на независимые компоненты, расположенные под прямым углом друг к другу. Таким образом, горизонтальную силу, направленную на северо-восток, можно разделить на две силы: одну, направленную на север, и другую, направленную на восток. Суммирование этих составляющих сил с помощью сложения векторов дает исходную силу. Разложение векторов силы на компоненты набора базисных векторов часто является более математически чистым способом описания сил, чем использование величин и направлений. Это связано с тем, что для ортогональных компонентов компоненты векторной суммы однозначно определяются скалярным сложением компонентов отдельных векторов. Ортогональные компоненты независимы друг от друга, поскольку силы, действующие под углом девяносто градусов друг к другу, не влияют на величину или направление друг друга. Выбор набора ортогональных базисных векторов часто осуществляется с учетом того, какой набор базисных векторов сделает математику наиболее удобной. Желателен выбор базисного вектора, направленного в том же направлении, что и одна из сил, поскольку тогда эта сила будет иметь только один ненулевой компонент. Ортогональные векторы силы могут быть трехмерными, при этом третий компонент находится под прямым углом к ​​двум другим.

Равновесие

Когда все силы, действующие на объект, уравновешены, говорят, что объект находится в состоянии равновесия . Следовательно, равновесие наступает, когда результирующая сила, действующая на точечную частицу, равна нулю (т. е. векторная сумма всех сил равна нулю). При работе с удлиненным телом также необходимо, чтобы чистый крутящий момент был равен нулю. Тело находится в статическом равновесии относительно системы отсчета, если оно покоится и не ускоряется, тогда как тело в динамическом равновесии движется с постоянной скоростью по прямой, т. е. движется, но не ускоряется. То, что один наблюдатель считает статическим равновесием, другой может видеть как динамическое равновесие, и наоборот.

Статический

Основные статьи: Статика и статическое равновесие

Статическое равновесие было понято задолго до изобретения классической механики. На объекты, которые не ускоряются, действует нулевая результирующая сила.

Простейший случай статического равновесия возникает, когда две силы равны по величине, но противоположны по направлению. Например, объект на ровной поверхности под действием силы тяжести тянется (притягивается) вниз к центру Земли. В то же время к поверхности прикладывается сила, которая противостоит силе, направленной вниз, равной силе, направленной вверх (называемой нормальной силой ). Эта ситуация создает нулевую результирующую силу и, следовательно, никакого ускорения.

Нажатие на объект, лежащий на поверхности трения, может привести к ситуации, когда объект не будет двигаться, поскольку приложенной силе противодействует статическое трение , возникающее между объектом и поверхностью стола. В ситуации отсутствия движения сила статического трения точно уравновешивает приложенную силу, что приводит к отсутствию ускорения. Статическое трение увеличивается или уменьшается в ответ на приложенную силу до верхнего предела, определяемого характеристиками контакта между поверхностью и объектом.

Статическое равновесие между двумя силами является наиболее распространенным способом измерения сил с использованием простых устройств, таких как весы и пружинные весы . Например, объект, подвешенный на вертикальных пружинных весах, испытывает силу тяжести, действующую на объект, уравновешиваемую силой, приложенной «силой реакции пружины», которая равна весу объекта. С помощью таких инструментов были открыты некоторые количественные законы силы: сила гравитации пропорциональна объему для объектов постоянной плотности (широко использовалась на протяжении тысячелетий для определения стандартных весов); Принцип Архимеда плавучести; Архимедом Анализ рычага ; закон Бойля для давления газа; и закон Гука для пружин. Все они были сформулированы и экспериментально проверены до того, как Исаак Ньютон изложил свои Три закона движения .

Динамический

Основная статья: Динамика (физика)

Галилео Галилей был первым, кто указал на внутренние противоречия, содержащиеся в описании сил Аристотелем.

Динамическое равновесие было впервые описано Галилеем , который заметил, что некоторые предположения аристотелевской физики противоречат наблюдениям и логике . Галилей понял, что простое сложение скоростей требует, чтобы понятия «абсолютной системы покоя » не существовало. Галилей пришел к выводу, что движение с постоянной скоростью полностью эквивалентно покою. Это противоречило идее Аристотеля о «естественном состоянии» покоя, к которому естественным образом приближаются объекты с массой. Простые эксперименты показали, что понимание Галилеем эквивалентности постоянной скорости и покоя было правильным. Например, если бы моряк уронил пушечное ядро ​​из «вороньего гнезда» корабля, движущегося с постоянной скоростью, согласно аристотелевской физике, ядро ​​упало бы прямо вниз, в то время как корабль двигался бы под ним. Таким образом, в аристотелевской вселенной падающее пушечное ядро ​​приземлилось бы за подножием мачты движущегося корабля. Когда этот эксперимент действительно проводится, ядро ​​всегда падает у подножия мачты, как будто оно знает, что оно должно путешествовать вместе с кораблем, несмотря на то, что оно отделено от него. Поскольку при падении к пушечному ядру не прилагается никакой направленной вперед горизонтальной силы, остается единственный вывод: ядро ​​продолжает двигаться с той же скоростью, что и лодка при падении. Таким образом, не требуется никакой силы, чтобы поддерживать движение пушечного ядра с постоянной скоростью вперед.

Более того, на любой объект, движущийся с постоянной скоростью, должна действовать нулевая результирующая сила (результирующая сила). Это определение динамического равновесия: когда все силы, действующие на объект, уравновешиваются, но он по-прежнему движется с постоянной скоростью. Простой случай динамического равновесия возникает при движении с постоянной скоростью по поверхности с кинетическим трением . В такой ситуации сила прикладывается в направлении движения, а кинетическая сила трения точно противодействует приложенной силе. Это приводит к нулевой чистой силе, но поскольку объект стартовал с ненулевой скоростью, он продолжает двигаться с ненулевой скоростью. Аристотель ошибочно истолковал это движение как вызванное приложенной силой. Если принять во внимание кинетическое трение, становится ясно, что нет результирующей силы, вызывающей движение с постоянной скоростью.

Примеры сил в классической механике

Некоторые силы являются следствием фундаментальных. В таких ситуациях для получения физического понимания можно использовать идеализированные модели. Например, каждый твердый объект считается твердым телом .

Гравитационный

Основная статья: Гравитация

Изображения свободно падающего баскетбольного мяча, снятые стробоскопом с частотой 20 вспышек в секунду. Единицы измерения расстояния справа кратны примерно 12 миллиметрам. Баскетбольный матч начинается в состоянии покоя. В момент первой вспышки (нулевая дистанция) он отпускается, после чего количество упавших единиц равно квадрату количества вспышек.

То, что мы сейчас называем гравитацией, не считалось универсальной силой до работ Исаака Ньютона. До Ньютона тенденция падения объектов на Землю не считалась связанной с движением небесных объектов. Галилей сыграл важную роль в описании характеристик падающих объектов, определив, что ускорение каждого объекта в свободном падении постоянно и не зависит от массы объекта. Сегодня это ускорение силы тяжести по отношению к поверхности Земли обычно обозначается как $\mathbf {g}$ и имеет величину около 9,81 метра в секунду в квадрате (это измерение берется на уровне моря и может варьироваться в зависимости от местоположения) и направлено к центру Земли. Это наблюдение означает, что сила гравитации, действующая на объект на поверхности Земли, прямо пропорциональна массе объекта. Таким образом, объект, имеющий массу $m$ испытает силу:

$$\mathbf {F} =m\mathbf {g} .$$

Для объекта, находящегося в свободном падении, этой силе нет сопротивления, и результирующая сила, действующая на объект, равна его весу. Для объектов, не находящихся в свободном падении, силе тяжести противостоят силы реакции, прикладываемые их опорами. Например, человек, стоящий на земле, испытывает нулевую чистую силу, поскольку нормальная сила (сила реакции) действует со стороны земли вверх на человека, которая уравновешивает его вес, направленный вниз.

Вклад Ньютона в теорию гравитации состоял в том, чтобы объединить движения небесных тел, которые, как предполагал Аристотель, находились в естественном состоянии постоянного движения, с падающим движением, наблюдаемым на Земле. Он предложил закон гравитации , который мог бы объяснить небесные движения, описанные ранее с использованием законов движения планет Кеплера .

Ньютон пришел к выводу, что на больших расстояниях эффекты гравитации можно наблюдать по-разному. В частности, Ньютон определил, что ускорение Луны вокруг Земли можно было бы приписать той же силе тяжести, если бы ускорение силы тяжести уменьшалось по закону обратных квадратов . Далее Ньютон понял, что ускорение тела под действием силы тяжести пропорционально массе другого притягивающего тела. Объединение этих идей дает формулу, связывающую массу ( $m_{\oplus }$) и радиус ( $R_{\oplus }$) Земли к ускорению свободного падения:

$$\mathbf {g} =-{\frac {Gm_{\oplus }}{{R_{\oplus }}^{2}}}{\hat {\mathbf {r} }},$$

где направление вектора определяется выражением ${\hat {\mathbf {r} }}$, — единичный вектор , направленный наружу от центра Земли.

В этом уравнении размерная константа $G$ используется для описания относительной силы тяжести. Эта константа стала известна как константа гравитации Ньютона , хотя ее значение было неизвестно при жизни Ньютона. Лишь в 1798 году Генри Кавендиш смог провести первое измерение $G$ использование торсионных весов ; об этом широко сообщалось в прессе как об измерении массы Земли с тех пор, как стало известно $G$ может позволить определить массу Земли с учетом приведенного выше уравнения. Ньютон понял, что, поскольку все небесные тела подчиняются одним и тем же законам движения , его закон тяготения должен быть универсальным. Вкратце, закон гравитации Ньютона гласит, что сила, действующая на сферический объект массы $m_{1}$ из-за гравитационного притяжения массы $m_{2}$ является

$$\mathbf {F} =-{\frac {Gm_{1}m_{2}}{r^{2}}}{\hat {\mathbf {r} }},$$

где $r$ расстояние между центрами масс двух объектов и ${\hat {\mathbf {r} }}$ — единичный вектор, направленный в направлении от центра первого объекта к центру второго объекта.

Эта формула была достаточно мощной, чтобы служить основой для всех последующих описаний движения в Солнечной системе вплоть до 20 века. В то время сложные методы анализа возмущений были изобретены для расчета отклонений орбит из-за влияния нескольких тел на планету , Луну , комету или астероид . Формализм был достаточно точным, чтобы позволить математикам предсказать существование планеты Нептун еще до того, как ее заметили.

Электромагнитный

Основная статья: Электромагнитная сила

Электростатическая сила была впервые описана Кулоном в 1784 году как сила, которая существует между двумя зарядами . Свойства электростатической силы заключались в том, что она изменялась по закону обратных квадратов, направленная в радиальном направлении , была одновременно притягивающей и отталкивающей (имелась внутренняя полярность ), не зависела от массы заряженных объектов и подчинялась принципу суперпозиции . Закон Кулона объединяет все эти наблюдения в одно краткое утверждение.

Последующие математики и физики обнаружили, что конструкция электрического поля полезна для определения электростатической силы, воздействующей на электрический заряд в любой точке пространства. Электрическое поле было основано на использовании гипотетического « пробного заряда » в любом месте пространства, а затем на использовании закона Кулона для определения электростатической силы. Таким образом, электрическое поле в любой точке пространства определяется как

$$\mathbf {E} ={\mathbf {F} \over {q}},$$

где $q$ — величина гипотетического испытательного заряда. Точно так же идея магнитного поля была введена, чтобы выразить, как магниты могут влиять друг на друга на расстоянии. Закон силы Лоренца определяет силу, действующую на тело с зарядом. $q$ из-за электрических и магнитных полей:

$$\mathbf {F} =q\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right),$$

где $\mathbf {F}$ это электромагнитная сила, $\mathbf {E}$ - электрическое поле в месте нахождения тела, $\mathbf {B}$ магнитное поле, а $\mathbf {v}$ - скорость частицы. Магнитный вклад в силу Лоренца представляет собой векторное произведение вектора скорости на магнитное поле.

Происхождение электрических и магнитных полей не было полностью объяснено до 1864 года, когда Джеймс Клерк Максвелл объединил ряд более ранних теорий в набор из 20 скалярных уравнений, которые позже были переформулированы в 4 векторных уравнения Оливером Хевисайдом и Джозайей Уиллардом Гиббсом . Эти « уравнения Максвелла » полностью описали источники полей как стационарные и движущиеся заряды, а также взаимодействия самих полей. Это привело Максвелла к открытию, что электрические и магнитные поля могут «самогенерироваться» посредством волны , движущейся со скоростью, которую он рассчитал как скорость света . Это понимание объединило зарождающиеся поля электромагнитной теории с оптикой и привело непосредственно к полному описанию электромагнитного спектра .

Нормальный

F _N представляет собой нормальную силу, действующую на объект.

Основная статья: Нормальная сила

Когда объекты находятся в контакте, сила, возникающая непосредственно между ними, называется нормальной силой и представляет собой компонент общей силы в системе, действующей перпендикулярно границе раздела между объектами. Нормальная сила тесно связана с третьим законом Ньютона. Например, нормальная сила отвечает за структурную целостность столов и полов, а также является силой, которая реагирует всякий раз, когда внешняя сила давит на твердый объект. Примером нормальной силы в действии является сила удара объекта, врезающегося в неподвижную поверхность.

Трение

Основная статья: Трение

Трение – это сила, противодействующая относительному движению двух тел. В макроскопическом масштабе сила трения напрямую связана с нормальной силой в точке контакта. Существуют две широкие классификации сил трения: статическое трение и кинетическое трение .

Статическая сила трения ( $\mathbf {F} _{\mathrm {sf} }$) будет точно противодействовать силам, приложенным к объекту, параллельному поверхности, до предела, определяемого коэффициентом статического трения ( $\mu _{\mathrm {sf} }$), умноженный на нормальную силу ( $\mathbf {F} _{\text{N}}$). Другими словами, величина статической силы трения удовлетворяет неравенству:

$$0\leq \mathbf {F} _{\mathrm {sf} }\leq \mu _{\mathrm {sf} }\mathbf {F} _{\mathrm {N} }.$$

Кинетическая сила трения ( $F_{\mathrm {kf} }$) обычно не зависит ни от приложенных сил, ни от движения объекта. Таким образом, величина силы равна:

$$\mathbf {F} _{\mathrm {kf} }=\mu _{\mathrm {kf} }\mathbf {F} _{\mathrm {N} },$$

где $\mu _{\mathrm {kf} }$ – коэффициент кинетического трения . Коэффициент кинетического трения обычно меньше коэффициента статического трения.

Напряжение

Основная статья: Напряжение (физика)

Силы натяжения можно моделировать с помощью идеальных струн, которые не имеют массы, не имеют трения, нерушимы и не растягиваются. Их можно комбинировать с идеальными блоками , которые позволяют идеальным струнам менять физическое направление. Идеальные струны мгновенно передают силы натяжения в парах действие-противодействие, так что если два объекта соединены идеальной струной, любая сила, направленная вдоль струны первым объектом, сопровождается силой, направленной вдоль струны в противоположном направлении вторым объектом. . Подсоединив одну и ту же веревку несколько раз к одному и тому же объекту с помощью конфигурации, в которой используются подвижные шкивы, можно увеличить силу натяжения груза. Для каждой струны, действующей на нагрузку, на нагрузку действует другой фактор силы натяжения струны. Такие машины обеспечивают механическое преимущество за счет соответствующего увеличения длины перемещаемой струны, необходимой для перемещения груза. Эти тандемные эффекты в конечном итоге приводят к сохранению механической энергии , поскольку работа, совершаемая над нагрузкой, одинакова, независимо от сложности машины.

Весна

Основные статьи: Эластичность (физика) и закон Гука

F _k – сила, реагирующая на нагрузку на пружину

Простая сила упругости возвращает пружину к ее естественной длине. Идеальная пружина считается безмассовой, лишенной трения, нерушимой и бесконечно растягивающейся. Такие пружины создают силы, которые толкают при сжатии или тянут при растяжении пропорционально смещению пружины от ее положения равновесия. Эта линейная зависимость была описана Робертом Гуком в 1676 году, в честь которого закон Гука назван . Если $\Delta x$ - перемещение, сила, действующая идеальной пружиной, равна:

$$\mathbf {F} =-k\Delta \mathbf {x} ,$$

где $k$ — это постоянная пружины (или постоянная силы), специфичная для пружины. Знак минус указывает на тенденцию силы действовать противоположно приложенной нагрузке.

Центростремительный

Основная статья: Центростремительная сила

Для объекта, находящегося в равномерном круговом движении , результирующая сила, действующая на объект, равна:

$$\mathbf {F} =-{\frac {mv^{2}}{r}}{\hat {\mathbf {r} }},$$

где $m$ это масса объекта, $v$ - скорость объекта и $r$ расстояние до центра кругового пути и ${\hat {\mathbf {r} }}$ - единичный вектор , направленный в радиальном направлении наружу от центра. Это означает, что результирующая сила, ощущаемая объектом, всегда направлена ​​к центру изогнутой траектории. Такие силы действуют перпендикулярно вектору скорости, связанной с движением объекта, и поэтому не меняют скорость объекта (величину скорости), а только направление вектора скорости. В более общем смысле, результирующую силу, ускоряющую объект, можно разделить на компонент, перпендикулярный пути, и компонент, касательный к пути. Это дает как тангенциальную силу, которая ускоряет объект, замедляя или ускоряя его, так и радиальную (центростремительную) силу, которая меняет его направление.

Механика сплошных сред

Когда сила сопротивления ( $\mathbf {F} _{\text{d}}$), связанное с сопротивлением воздуха, становится равным по величине силе тяжести на падающем объекте ( $\mathbf {F} _{\text{g}}$), объект достигает состояния динамического равновесия при конечной скорости .

Основные статьи: Давление , Сопротивление (физика) и Напряжение (механика).

Законы Ньютона и ньютоновская механика в целом были впервые разработаны для описания того, как силы влияют на идеализированные точечные частицы, а не на трехмерные объекты. В реальной жизни материя имеет расширенную структуру, и силы, действующие на одну часть объекта, могут влиять на другие части объекта. В ситуациях, когда решетка, удерживающая вместе атомы в объекте, может течь, сжиматься, расширяться или иным образом менять форму, теории механики сплошной среды описывают, как силы влияют на материал. Например, в протяженных жидкостях разница в давлении приводит к тому, что силы направляются вдоль градиентов давления следующим образом:

$${\frac {\mathbf {F} }{V}}=-\mathbf {\nabla } P,$$

где $V$ - объем объекта в жидкости и $P$ — скалярная функция , описывающая давление во всех точках пространства. Градиенты и перепады давления приводят к выталкивающей силе для жидкостей, взвешенных в гравитационных полях, ветрам в науке об атмосфере и подъемной силе , связанной с аэродинамикой и полетом .

Конкретным примером такой силы, связанной с динамическим давлением, является сопротивление жидкости: объемная сила, которая сопротивляется движению объекта через жидкость из-за вязкости . При так называемом « сопротивлении Стокса » сила примерно пропорциональна скорости, но противоположна по направлению:

$$\mathbf {F} _{\mathrm {d} }=-b\mathbf {v} ,$$

где:

• $b$ — константа, зависящая от свойств жидкости и размеров объекта (обычно площади поперечного сечения ), а
• $\mathbf {v}$ это скорость объекта.

Более формально, силы в механике сплошной среды полностью описываются тензором с напряжений членами, которые грубо определяются как

$$\sigma ={\frac {F}{A}},$$

где $A$ – соответствующая площадь поперечного сечения объема, для которого рассчитывается тензор напряжений. Этот формализм включает члены давления, связанные с силами, которые действуют нормально к площади поперечного сечения ( матричные диагонали тензора), а также члены сдвига , связанные с силами, которые действуют параллельно площади поперечного сечения (недиагональные элементы). Тензор напряжений учитывает силы, вызывающие все напряжения (деформации), включая также растягивающие напряжения и сжатия .

Фиктивный

Основная статья: Фиктивные силы

Существуют силы, зависящие от системы координат , то есть они появляются вследствие принятия неньютоновских (то есть неинерциальных ) систем отсчета . К таким силам относятся центробежная сила и сила Кориолиса . Эти силы считаются фиктивными, поскольку они не существуют в системах отсчета, не имеющих ускорения. Поскольку эти силы не являются подлинными, их также называют «псевдосилами».

В общей теории относительности гравитация становится фиктивной силой, возникающей в ситуациях, когда пространство-время отклоняется от плоской геометрии.

основанные на

Вращение и крутящий момент

Связь между силой ( F ), крутящим моментом ( τ ) и количества движения векторами ( p и L ) во вращающейся системе.

Основная статья: Крутящий момент

Силы, которые заставляют вращаться протяженные объекты, связаны с крутящими моментами . Математически момент силы $\mathbf {F}$ определяется относительно произвольной контрольной точки как векторное произведение :

$${\boldsymbol {\tau }}=\mathbf {r} \times \mathbf {F} ,$$

где $\mathbf {r}$ – вектор положения точки приложения силы относительно опорной точки.

Крутящий момент является эквивалентом силы при вращении, точно так же, как угол является эквивалентом вращения для положения , угловая скорость для скорости и угловой момент для импульса . Как следствие первого закона движения Ньютона, существует инерция вращения , которая гарантирует, что все тела сохраняют свой угловой момент, если на них не действует несбалансированный крутящий момент. Точно так же второй закон движения Ньютона можно использовать для вывода аналогичного уравнения для мгновенного углового ускорения твердого тела:

$${\boldsymbol {\tau }}=I{\boldsymbol {\alpha }},$$

где

• $I$ это момент инерции тела
• ${\boldsymbol {\alpha }}$ – угловое ускорение тела.

Это дает определение момента инерции, который является вращательным эквивалентом массы. В более продвинутых трактовках механики, где описывается вращение в течение определенного интервала времени, момент инерции должен быть заменен тензором , который при правильном анализе полностью определяет характеристики вращения, включая прецессию и нутацию .

Аналогично, дифференциальная форма Второго закона Ньютона дает альтернативное определение крутящего момента:

$${\boldsymbol {\tau }}={\frac {\mathrm {d} \mathbf {L} }{\mathrm {dt} }},$$

где $\mathbf {L}$ - угловой момент частицы.

Третий закон движения Ньютона требует, чтобы все объекты, создающие крутящие моменты, сами испытывали равные и противоположные крутящие моменты. и, следовательно, также напрямую подразумевает сохранение углового момента для закрытых систем, которые испытывают вращения и обороты под действием внутренних моментов.

Янк

Рывок . определяется как скорость изменения силы

$\mathbf {Y} ={\frac {d\mathbf {F} }{dt}}$

Этот термин используется в биомеханическом анализе. спортивная оценка и роботизированное управление. Вторая (называемая «перетягивание»), третья («рывок»), четвертая («встряска») и высшие производные используются редко.

Кинематические интегралы

Основные статьи: Импульс , Механическая работа и Мощность (физика)

Силы можно использовать для определения ряда физических понятий путем интегрирования по кинематическим переменным . Например, интегрирование по времени дает определение импульса :

$$\mathbf {J} =\int _{t_{1}}^{t_{2}}{\mathbf {F} \,\mathrm {d} t},$$

что согласно Второму закону Ньютона должно быть эквивалентно изменению импульса (что приводит к теореме об импульсном импульсе ).

Аналогично, интегрирование по положению дает определение работы , совершаемой силой:

$$W=\int _{\mathbf {x} _{1}}^{\mathbf {x} _{2}}{\mathbf {F} \cdot {\mathrm {d} \mathbf {x} }},$$

что эквивалентно изменению кинетической энергии (что приводит к теореме об энергии работы ).

Мощность P — это скорость изменения d W /d t работы W при траектории за счет изменения положения. удлинении $d\mathbf {x}$ за интервал времени d t :

$$\mathrm {d} W={\frac {\mathrm {d} W}{\mathrm {d} \mathbf {x} }}\cdot \mathrm {d} \mathbf {x} =\mathbf {F} \cdot \mathrm {d} \mathbf {x} ,$$

так

$$P={\frac {\mathrm {d} W}{\mathrm {d} t}}={\frac {\mathrm {d} W}{\mathrm {d} \mathbf {x} }}\cdot {\frac {\mathrm {d} \mathbf {x} }{\mathrm {d} t}}=\mathbf {F} \cdot \mathbf {v} ,$$

с $\mathbf {v} =\mathrm {d} \mathbf {x} /\mathrm {d} t$ скорость ​ .

энергия

Основная статья: Потенциальная энергия

Вместо силы часто потенциальной энергии используется математически связанное понятие поля . Например, гравитационную силу, действующую на объект, можно рассматривать как действие гравитационного поля , присутствующего в месте расположения объекта. Математически переформулировав определение энергии (через определение работы ), потенциальное скалярное поле $U(\mathbf {r} )$ определяется как поле, градиент которого равен и противоположен силе, создаваемой в каждой точке:

$$\mathbf {F} =-\mathbf {\nabla } U.$$

Силы можно разделить на консервативные и неконсервативные. Консервативные силы эквивалентны градиенту потенциала , а неконсервативные силы — нет.

Сохранение

Основная статья: Консервативная сила

Консервативная сила, действующая на закрытую систему, имеет связанную с ней механическую работу, которая позволяет энергии преобразовываться только между кинетическими или потенциальными формами. Это означает, что для закрытой системы чистая механическая энергия сохраняется всякий раз, когда на систему действует консервативная сила. Таким образом, сила напрямую связана с разницей потенциальной энергии между двумя разными точками пространства. и может рассматриваться как артефакт потенциального поля точно так же, как направление и величина потока воды можно рассматривать как артефакт контурной карты высоты местности.

Консервативные силы включают гравитацию , электромагнитную силу и силу пружины . У каждой из этих сил есть модели, которые зависят от положения, которое часто задается в виде радиального вектора. $\mathbf {r}$ исходящие из сферически-симметричных потенциалов. Примеры этого следующие:

Для гравитации:

$$\mathbf {F} _{\text{g}}=-{\frac {Gm_{1}m_{2}}{r^{2}}}{\hat {\mathbf {r} }},$$

где $G$ гравитационная постоянная , а $m_{n}$ — масса объекта n .

Для электростатических сил:

$$\mathbf {F} _{\text{e}}={\frac {q_{1}q_{2}}{4\pi \varepsilon _{0}r^{2}}}{\hat {\mathbf {r} }},$$

где $\varepsilon _{0}$ – электрическая проницаемость свободного пространства , $q_{n}$ — электрический заряд объекта n .

Для пружинных сил:

$$\mathbf {F} _{\text{s}}=-kr{\hat {\mathbf {r} }},$$

где $k$ это константа пружины .

Для некоторых физических сценариев невозможно смоделировать силы, возникающие вследствие простого градиента потенциалов. Это часто происходит из-за макроскопического статистического среднего микросостояний . Например, статическое трение вызвано градиентами многочисленных электростатических потенциалов между атомами , но проявляется как силовая модель, независимая от какого-либо вектора положения на макромасштабе. Неконсервативные силы, помимо трения, включают другие контактные силы , растяжение , сжатие и сопротивление . При любом достаточно подробном описании все эти силы являются результатами консервативных, поскольку каждая из этих макроскопических сил является чистым результатом градиентов микроскопических потенциалов.

Связь между макроскопическими неконсервативными силами и микроскопическими консервативными силами описывается детальным рассмотрением с помощью статистической механики . В макроскопических закрытых системах неконсервативные силы изменяют внутреннюю энергию системы и часто связаны с переносом тепла. Согласно Второму закону термодинамики , неконсервативные силы обязательно приводят к преобразованиям энергии внутри закрытых систем из упорядоченного состояния в более случайное по мере увеличения энтропии .

Единицы

Единицей системе СИ силы в является ньютон (символ Н), который представляет собой силу, необходимую для ускорения массы в один килограмм со скоростью один метр в секунду в квадрате, или кг·м·с. ⁻² .Соответствующей СГС единицей является дина , сила, необходимая для ускорения массы в один грамм на один сантиметр в секунду в квадрате, или г·см·с. ⁻² . Таким образом, ньютон равен 100 000 дин.

Гравитационная фут-фунт-секунда английской единицы силы — фунт-сила (фунт-сила), определяемая как сила, действующая под действием силы тяжести на фунт массы в стандартном гравитационном поле 9,80665 м·с. ⁻² . Фунт-сила представляет собой альтернативную единицу измерения массы: одна пуля — это масса, которая ускоряется на один фут в секунду в квадрате под воздействием одной фунт-силы. Альтернативной единицей силы в другой системе фут-фунт-секунда, абсолютной системе fps, является паундал , определяемый как сила, необходимая для ускорения массы в один фунт со скоростью один фут в секунду в квадрате.

Фунт-сила имеет метрический аналог, который используется реже, чем ньютон: килограмм-сила (кгс) (иногда килопонд) — это сила, действующая стандартной гравитацией на один килограмм массы. Килограмм-сила приводит к альтернативной, но редко используемой единице массы: метрическая пуля (иногда кружка или хил) — это масса, которая ускоряется со скоростью 1 м·с. ⁻² при приложении силы 1 кгс. Килограмм-сила не является частью современной системы СИ и, как правило, устарела, иногда используется для выражения веса самолета, реактивной тяги, натяжения велосипедных спиц, настроек динамометрического ключа и выходного крутящего момента двигателя.

Единицы силы

	Ньютон	дина	килограмм-сила , килопонд	фунт-сила	фунт
1 Н	≡ 1   кг⋅м/с 2	= 10 5  мужчина	≈ 0,10197   кп	≈ 0,22481   фунт-сила	≈ 7,2330   фунтов
1   человек	=  10 –5  Н	≡   1   г⋅см/с 2	≈  1.0197 × 10 −6  КП	≈  2.2481 × 10 −6  фунт-сила	≈  7.2330 × 10 −5  пдл
1   кп	=   9,80665   Н	=   980665   дина	≡  g n  ×  1  kg	≈   2,2046   фунт-сила	≈   70,932   фунтов
1 фунт-сила	≈   4,448222   Н	≈  444822  dyn	≈   0,45359   кп	≡  g n  ×  1  lb	≈   32,174   фунта
1   пдл	≈   0,138255   Н	≈  13825  dyn	≈   0,014098   кп	≈   0,031081   фунт-сила	≡   1   фунт⋅ фут /с 2
Значение g n , используемое в официальном определении килограмм-силы (9,80665 м/с). 2 ) используется здесь для всех гравитационных единиц.

См. также Тонна-сила .

Пересмотр концепции сил

В начале 20-го века появились новые физические идеи для объяснения экспериментальных результатов в астрономической и субмикроскопической областях. Как обсуждается ниже, теория относительности меняет определение импульса, а квантовая механика повторно использует понятие «силы» в микроскопическом контексте, где законы Ньютона не применяются напрямую.

Специальная теория относительности

Основная статья: Релятивистская механика § Сила

В специальной теории относительности масса и энергия эквивалентны (в этом можно убедиться, вычислив работу, необходимую для ускорения объекта). Когда скорость объекта увеличивается, увеличивается и его энергия и, следовательно, его эквивалент массы (инерция). Таким образом, для ускорения на ту же величину требуется больше силы, чем при более низкой скорости. Второй закон Ньютона,

$$\mathbf {F} ={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}},$$

остается действительным, поскольку это математическое определение. Но чтобы импульс сохранялся при релятивистской относительной скорости, $v$, импульс необходимо переопределить как:

$$\mathbf {p} ={\frac {m_{0}\mathbf {v} }{\sqrt {1-v^{2}/c^{2}}}},$$

где $m_{0}$ это масса покоя и $c$ скорость света .

Выражение, связывающее силу и ускорение для частицы с постоянной ненулевой массой покоя $m$ переезд в $x$ направление со скоростью $v$ является:

$$\mathbf {F} =\left(\gamma ^{3}ma_{x},\gamma ma_{y},\gamma ma_{z}\right),$$

где

$$\gamma ={\frac {1}{\sqrt {1-v^{2}/c^{2}}}}.$$

называется фактором Лоренца . Фактор Лоренца резко возрастает по мере приближения относительной скорости к скорости света. Следовательно, для создания того же ускорения при предельной скорости необходимо прикладывать все большую и большую силу. Относительная скорость не может достигать $c$. Если $v$ очень мал по сравнению с $c$, затем $\gamma$ очень близко к 1 и

$$\mathbf {F} =m\mathbf {a}$$

является близким приближением. Даже для использования в теории относительности можно восстановить форму

$$F^{\mu }=mA^{\mu }$$

за счет использования четырехвекторов . Это соотношение верно в теории относительности, когда $F^{\mu }$ это четыре силы , $m$ – инвариантная масса , а $A^{\mu }$ это четырехкратное ускорение .

Общая . теория относительности включает в себя более радикальный отход от ньютоновского подхода к силе, особенно к гравитационной силе Это переосмысление природы гравитации более подробно описано ниже .

Квантовая механика

Основные статьи: Квантовая механика и принцип исключения Паули

Квантовая механика — это теория физики, первоначально разработанная для понимания микроскопических явлений: поведения на уровне молекул, атомов или субатомных частиц. Грубо говоря, чем меньше система, тем больше адекватная математическая модель требует понимания квантовых эффектов. Концептуальная основа квантовой физики отличается от классической физики. Вместо того, чтобы думать о таких величинах, как положение, импульс и энергия, как о свойствах объекта , нужно учитывать, какой результат может появиться при выполнении измерения выбранного типа. Квантовая механика позволяет физику рассчитать вероятность того, что выбранное измерение приведет к определенному результату. Ожидаемое значение измерения представляет собой среднее значение возможных результатов, которые оно может дать, взвешенное по вероятностям их появления.

В квантовой механике взаимодействия обычно описываются с точки зрения энергии, а не силы. Теорема Эренфеста обеспечивает связь между значениями квантового ожидания и классической концепцией силы, связь, которая обязательно является неточной, поскольку квантовая физика фундаментально отличается от классической. В квантовой физике правило Борна используется для расчета ожидаемых значений измерения положения или измерения импульса. Эти ожидаемые значения обычно меняются со временем; то есть в зависимости от времени, в которое (например) производится измерение положения, вероятности различных его возможных результатов будут различаться. Теорема Эренфеста, грубо говоря, гласит, что уравнения, описывающие, как эти ожидаемые значения изменяются с течением времени, имеют форму, напоминающую второй закон Ньютона, где сила определяется как отрицательная производная потенциальной энергии. Однако чем более выражены квантовые эффекты в данной ситуации, тем труднее сделать из этого сходства осмысленные выводы.

Квантовая механика также вводит два новых ограничения, которые взаимодействуют с силами субмикроскопического масштаба и которые особенно важны для атомов. Несмотря на сильное притяжение ядра, принцип неопределенности ограничивает минимальную степень распределения вероятностей электронов. а принцип Паули не позволяет электронам иметь одно и то же распределение вероятностей. Это порождает возникающее давление, известное как давление вырождения . Динамическое равновесие между давлением вырождения и электромагнитной силой притяжения придает атомам, молекулам, жидкостям и твердым телам стабильность .

Квантовая теория поля

Основная статья: Квантовая теория поля

Диаграмма Фейнмана распада нейтрона на протон. находится W-бозон между двумя вершинами, что указывает на отталкивание.

В современной физике элементарных частиц силы и ускорение частиц объясняются как математический побочный продукт обмена калибровочными бозонами , несущими импульс . С развитием квантовой теории поля и общей теории относительности стало понятно, что сила — это избыточное понятие, возникающее из-за сохранения импульса ( 4-импульса в теории относительности и импульса виртуальных частиц в квантовой электродинамике ). Сохранение импульса может быть напрямую выведено из однородности или симметрии пространства и поэтому обычно считается более фундаментальным , чем концепция силы. Таким образом, известные в настоящее время фундаментальные силы правильнее считать « фундаментальными взаимодействиями ».

Хотя для детального предсказания результата таких взаимодействий необходимы сложные математические описания, существует концептуально простой способ их описания с помощью диаграмм Фейнмана . На диаграмме Фейнмана каждая частица материи представлена ​​в виде прямой линии (см. мировую линию ), путешествующей во времени, которая обычно увеличивается вверх или вправо на диаграмме. Частицы материи и антиматерии идентичны, за исключением направления их распространения по диаграмме Фейнмана. Мировые линии частиц пересекаются в вершинах взаимодействия , и диаграмма Фейнмана представляет любую силу, возникающую в результате взаимодействия, возникающую в вершине, с соответствующим мгновенным изменением направления мировых линий частицы. Калибровочные бозоны испускаются из вершины в виде волнистых линий и в случае виртуального обмена частицами поглощаются в соседней вершине. Полезность диаграмм Фейнмана состоит в том, что с помощью тех же правил можно описать и другие типы физических явлений, входящие в общую картину фундаментальных взаимодействий , но концептуально отделенные от сил. Например, диаграмма Фейнмана может в кратких деталях описать, как нейтрон распадается на электрон , протон и антинейтрино — взаимодействие, опосредованное тем же калибровочным бозоном, который отвечает за слабое ядерное взаимодействие .

Фундаментальные взаимодействия

Основная статья: Фундаментальное взаимодействие

Все известные силы Вселенной подразделяются на четыре фундаментальных взаимодействия . Сильное слабое и взаимодействия действуют только на очень коротких расстояниях и ответственны за взаимодействия между субатомными частицами , включая нуклоны и составные ядра . Электромагнитная сила действует между электрическими зарядами , а гравитационная сила действует между массами . Все остальные силы в природе происходят из этих четырех фундаментальных взаимодействий, действующих в рамках квантовой механики , включая ограничения, введенные уравнением Шредингера и принципом исключения Паули . Например, трение – это проявление электромагнитной силы, действующей между атомами двух поверхностей. Силы в пружинах , моделируемые законом Гука , также являются результатом электромагнитных сил. Центробежные силы — это силы ускорения , возникающие просто из-за ускорения вращающихся систем отсчета .

Фундаментальные теории сил возникли в результате объединения различных идей. Например, универсальная теория гравитации Ньютона показала, что сила, ответственная за падение объектов вблизи поверхности Земли , является также силой, ответственной за падение небесных тел вокруг Земли ( Луны ) и вокруг Солнца (планет). Майкл Фарадей и Джеймс Клерк Максвелл продемонстрировали, что электрические и магнитные силы были объединены посредством теории электромагнетизма. В 20 веке развитие квантовой механики привело к современному пониманию того, что первые три фундаментальные силы (все, кроме гравитации) являются проявлениями материи ( фермионов ), взаимодействующей путем обмена виртуальными частицами, называемыми калибровочными бозонами . Эта Стандартная модель физики элементарных частиц предполагает сходство между силами и побудила ученых предсказать объединение слабых и электромагнитных взаимодействий в электрослабой теории, что впоследствии было подтверждено наблюдениями.

Четыре фундаментальные силы природы

Свойство/Взаимодействие	Гравитация	Слабый	Электромагнитный	Сильный
		(Электрослабый)		Фундаментальный	Остаточный
Действует на:	Масса - Энергия	Вкус	Электрический заряд	Цветовой заряд	Атомные ядра
Частицы испытывают:	Все	Кварки, лептоны	Электрически заряженный	Кварки, Глюоны	Адроны
Частицы, опосредующие:	Гравитация (пока не наблюдалось)	В + В − С 0	с	Глюоны	Мезоны
Сила в шкале кварков:	10 −41	10 −4	1	60	Непригодный к кваркам
Сила в масштабе протоны/нейтроны:	10 −36	10 −7	1	Непригодный адронам	20

Гравитационный

Такие инструменты, как GRAVITY, представляют собой мощный зонд для обнаружения силы гравитации.

Закон тяготения Ньютона является примером действия на расстоянии : одно тело, например Солнце, оказывает влияние на любое другое тело, например на Землю, независимо от того, насколько далеко они друг от друга находятся. Причем это действие на расстоянии мгновенное. Согласно теории Ньютона, изменение положения одного тела меняет гравитационное притяжение, ощущаемое всеми другими телами в один и тот же момент времени. Альберт Эйнштейн признал, что это несовместимо со специальной теорией относительности и ее предсказанием о том, что воздействия не могут распространяться быстрее скорости света . Итак, он искал новую теорию гравитации, которая была бы релятивистски последовательной. Орбита Меркурия не соответствовала предсказанной законом гравитации Ньютона. Некоторые астрофизики предсказывали существование неоткрытой планеты ( Вулкан ), которая могла бы объяснить расхождения. Когда Эйнштейн сформулировал свою теорию общей теории относительности (ОТО), он сосредоточился на проблемной орбите Меркурия и обнаружил, что его теория добавила поправку, которая могла бы объяснить несоответствие . Это был первый случай, когда теория гравитации Ньютона оказалась неточной.

С тех пор общая теория относительности была признана теорией, лучше всего объясняющей гравитацию. В ОТО гравитация не рассматривается как сила, а, скорее, объекты, свободно движущиеся в гравитационных полях, перемещаются по собственной инерции по прямым линиям через искривленное пространство-время , определяемое как кратчайший пространственно-временной путь между двумя пространственно-временными событиями. С точки зрения объекта все движение происходит так, как если бы гравитации не было вообще. Только при наблюдении за движением в глобальном смысле можно наблюдать искривление пространства-времени и определять силу на основе искривленной траектории объекта. Таким образом, прямая линия в пространстве-времени рассматривается как кривая линия в пространстве и называется баллистической траекторией объекта. Например, баскетбольный мяч брошенный с земли движется по параболе , так как находится в однородном гравитационном поле. Ее пространственно-временная траектория представляет собой почти прямую линию, слегка изогнутую (с радиусом кривизны порядка нескольких световых лет ). Производная по времени изменяющегося импульса объекта — это то, что мы называем «гравитационной силой».

Электромагнитный

Уравнения Максвелла и набор методов, построенных на их основе, адекватно описывают широкий спектр физических явлений, связанных с силой в электричестве и магнетизме. Эта классическая теория уже включает эффекты относительности. Понимание квантованных электромагнитных взаимодействий между элементарными частицами требует квантовой электродинамики (или КЭД). В КЭД фотоны являются фундаментальными обменными частицами, описывающими все взаимодействия, относящиеся к электромагнетизму, включая электромагнитную силу.

Сильное ядерное оружие

Основная статья: Сильное взаимодействие

Есть две «ядерные силы», которые сегодня обычно описываются как взаимодействия, имеющие место в квантовых теориях физики элементарных частиц. Сильное ядерное взаимодействие — это сила, ответственная за структурную целостность атомных ядер , и получившее свое название из-за своей способности преодолевать электромагнитное отталкивание между протонами.

Сегодня считается, что сильное взаимодействие представляет собой взаимодействие между кварками и глюонами , подробно описанное теорией квантовой хромодинамики (КХД). Сильное взаимодействие — это фундаментальная сила , опосредованная глюонами, действующая на кварки, антикварки и сами глюоны. Сильная сила действует только непосредственно на элементарные частицы. в атомных ядрах) наблюдается остаток Между адронами (в частности, нуклонами , известный как ядерная сила . Здесь сильное взаимодействие действует косвенно, передаваемое через глюоны, входящие в состав виртуальных пи- и ро- мезонов , классических передатчиков ядерного взаимодействия. Неудача многих поисков свободных кварков показала, что затронутые элементарные частицы невозможно наблюдать напрямую. Это явление называется ограничением цвета .

Слабое ядерное

Основная статья: Слабое взаимодействие

Уникальное среди фундаментальных взаимодействий слабое ядерное взаимодействие не создает связанных состояний. Слабое взаимодействие обусловлено обменом тяжелыми W- и Z-бозонами . Поскольку слабое взаимодействие опосредовано двумя типами бозонов, его можно разделить на два типа взаимодействия или « вершины » — заряженный ток , в котором участвуют электрически заряженные W ⁺ и В ⁻ бозоны и нейтральный ток с участием электрически нейтрального Z ⁰ бозоны. Самый известный эффект слабого взаимодействия — это бета-распад (нейтронов в атомных ядрах) и связанная с ним радиоактивность . Это тип взаимодействия заряженных токов. Слово «слабый» происходит от того факта, что напряженность поля составляет около 10 ¹³ раз меньше, чем у сильного взаимодействия . Тем не менее, на коротких расстояниях он сильнее гравитации. Также была разработана последовательная электрослабая теория, которая показывает, что электромагнитные силы и слабое взаимодействие неразличимы при температурах, превышающих примерно 10°С. ¹⁵  К. ​ Такие температуры имели место при столкновениях плазмы в первые моменты Большого взрыва .

См. также

• Контактная сила - сила между двумя объектами, находящимися в физическом контакте.
• Управление усилием – управление усилием осуществляется машиной.
• Датчик силы - Прибор для измерения силы.
• Порядки величины (силы) - Сравнение широкого спектра физических сил.
• Система параллельных сил – Ситуация в машиностроении
• Твердое тело - физический объект, который не деформируется под воздействием на него сил или моментов.
• Удельная сила - Понятие в физике.

Внешние ссылки

• «Классическая механика, неделя 2: Законы Ньютона» . MIT OpenCourseWare . Проверено 9 августа 2023 г.
• «Основы физики I, Лекция 3: Законы движения Ньютона» . Открытые курсы Йельского университета . Проверено 9 августа 2023 г.