Подъем (сила)

Чтобы узнать о других значениях, см. Лифт (значения) .

1902 года Планер Райта демонстрирует свою подъемную силу, подтягиваясь вверх.

Когда жидкость обтекает объект, она оказывает силу на объект . Подъемная сила — это составляющая этой силы, перпендикулярная направлению набегающего потока. Она контрастирует с силой сопротивления , которая является составляющей силы, параллельной направлению потока. Обычно подъемная сила действует в направлении вверх, чтобы противостоять силе тяжести , но определено, что она действует перпендикулярно потоку и, следовательно, может действовать в любом направлении.

Если окружающей жидкостью является воздух, эта сила называется аэродинамической силой . В воде или любой другой жидкости это называется гидродинамической силой .

Динамический подъем отличается от других видов подъемной силы в жидкостях. Аэростатическая подъемная сила или плавучесть , при которой внутренняя жидкость легче окружающей жидкости, не требует движения и используется на воздушных шарах, дирижаблях, дирижаблях, лодках и подводных лодках. Глиссирующий подъемник , при котором в поток жидкости погружена только нижняя часть тела, применяется на моторных лодках, досках для серфинга, виндсерферах, парусных лодках и водных лыжах.

Обзор

Подъемная сила определяется как составляющая аэродинамической силы , перпендикулярная направлению потока, а сопротивление - это составляющая, параллельная направлению потока.

Жидкость , обтекающая поверхность твердого объекта, оказывает на него силу . Не имеет значения, движется ли объект в неподвижной жидкости (например, самолет, летящий по воздуху), или объект неподвижен, а жидкость движется (например, крыло в аэродинамической трубе), или оба движутся (например, парусник, использующий ветер для движения вперед). Подъемная сила — это составляющая этой силы, перпендикулярная направлению набегающего потока. Подъёмная сила всегда сопровождается силой сопротивления , которая является составляющей поверхностной силы, параллельной направлению потока.

Подъемная сила в основном связана с крыльями самолетов обтекаемыми , хотя она чаще создается многими другими телами , такими как пропеллеры , воздушные змеи , винты вертолетов , крылья гоночных автомобилей , морские паруса , ветряные турбины , а также парусников килями , корабельными рулями. , и подводные крылья в воде. Подъемник также используется летающими и планирующими животными , особенно птицами , летучими мышами и насекомыми , и даже в растительном мире семенами некоторых деревьев. Хотя общее значение слова « лифт » предполагает, что подъемная сила противостоит весу, подъемная сила может быть в любом направлении относительно силы тяжести, поскольку она определяется относительно направления потока, а не направления силы тяжести. Когда самолет движется по прямой и горизонтальной траектории, большая часть подъемной силы противодействует силе тяжести. Однако, когда самолет набирает высоту , снижается или выполняет поворот, подъемная сила наклоняется относительно вертикали. Подъемная сила также может действовать как прижимная сила в некоторых фигурах высшего пилотажа или на крыле гоночного автомобиля. Лифт также может быть в основном горизонтальным, например, на парусном судне.

Подъемная сила, обсуждаемая в этой статье, в основном относится к аэродинамическим профилям, хотя морские крылья на подводных крыльях и гребные винты имеют одни и те же физические принципы и работают одинаково, несмотря на различия между воздухом и водой, такие как плотность, сжимаемость и вязкость.

Обтекание поднимающегося профиля представляет собой явление механики жидкости , которое можно понять по существу на двух уровнях: существуют математические теории , которые основаны на установленных законах физики и точно представляют поток, но требуют решения уравнений в частных производных. И есть физические объяснения без математики, которые менее строги. Правильно объяснить подъем в этих качественных терминах сложно, поскольку связанные с этим причинно-следственные связи неуловимы. , Исчерпывающее объяснение охватывающее все существенные аспекты, обязательно является сложным. Существует также множество упрощенных объяснений , но все они оставляют необъясненными значительные части явления, а в некоторых также есть элементы, которые просто неверны.

Упрощенное физическое объяснение подъемной силы на аэродинамическом профиле.

Поперечное сечение крыла определяет форму аэродинамического профиля.

Аэродинамический профиль представляет собой обтекаемую форму, способную создавать значительно большую подъемную силу, чем сопротивление. Плоская пластина может создавать подъемную силу, но не такую ​​большую, как обтекаемый профиль, и с несколько большим сопротивлением.Большинство упрощенных объяснений следуют одному из двух основных подходов, основанных либо на законах движения Ньютона , либо на принципе Бернулли .

Объяснение на основе отклонения потока и законов Ньютона.

Когда крыло создает подъемную силу, оно отклоняет воздух вниз, и для этого оно должно оказывать на воздух нисходящую силу. Третий закон Ньютона требует, чтобы воздух оказывал на крыло равную направленную вверх силу.

Профиль создает подъемную силу, оказывая нисходящую силу на воздух, проходящий мимо. Согласно третьему закону Ньютона , воздух должен оказывать на аэродинамический профиль равную и противоположную (вверх) силу, которая и есть подъемная сила.

Когда воздушный поток приближается к аэродинамическому профилю, он изгибается вверх, но, проходя через аэродинамический профиль, он меняет направление и следует по траектории, изогнутой вниз. Согласно второму закону Ньютона, это изменение направления потока требует направленной вниз силы, приложенной к воздуху со стороны аэродинамического профиля. Тогда третий закон Ньютона требует, чтобы воздух оказывал направленную вверх силу на крыло; таким образом, создается сила реакции, подъемная сила, противоположная изменению направления. В случае крыла самолета крыло оказывает направленную вниз силу на воздух, а воздух оказывает направленную вверх силу на крыло.

Поворот потока вниз производится не только нижней поверхностью аэродинамического профиля, и поток воздуха над аэродинамическим профилем отвечает за большую часть поворота вниз.

Это объяснение верно, но оно неполно. Это не объясняет, как аэродинамический профиль может придавать поворот вниз гораздо более глубокой полосе потока, чем она на самом деле касается. Более того, в нем не упоминается, что подъемная сила создается за счет разницы давлений , и не объясняется, как поддерживается эта разница давлений.

Споры относительно эффекта Коанды

Основная статья: Эффект Коанды

Некоторые версии объяснения подъемной силы с помощью отклонения потока ссылаются на эффект Коанды как на причину, по которой поток может следовать за выпуклой верхней поверхностью профиля. Традиционное определение в области аэродинамики заключается в том, что эффект Коанды относится к тенденции струи жидкости оставаться прикрепленной к прилегающей поверхности, которая отклоняется от потока, и, как следствие, к вовлечению окружающего воздуха в поток.

В более широком смысле, некоторые считают, что этот эффект включает тенденцию любого пограничного слоя жидкости прилипать к искривленной поверхности, а не только пограничного слоя, сопровождающего струю жидкости. Именно в этом более широком смысле эффект Коанды используется в некоторых популярных источниках для объяснения того, почему воздушный поток остается прикрепленным к верхней стороне аэродинамического профиля. Это спорное использование термина «эффект Коанды»; поток, следующий за верхней поверхностью, просто отражает отсутствие отрыва пограничного слоя, поэтому он не является примером эффекта Коанды. Независимо от того, применимо ли это более широкое определение «эффекта Коанды», название «эффект Коанды» не дает объяснения, а просто дает явлению имя.

Способность потока жидкости следовать по криволинейной траектории не зависит от сдвиговых сил, вязкости жидкости или наличия пограничного слоя. Воздух, обтекающий профиль, прилипающий как к верхней, так и к нижней поверхностям и создающий подъемную силу, считается явлением невязкого потока.

Объяснения, основанные на увеличении скорости потока и принципе Бернулли.

Есть две распространенные версии этого объяснения: одна основана на «равном времени прохождения», а другая — на «препятствии» воздушному потоку.

Иллюстрация неправильного объяснения подъемной силы профиля, равного времени прохождения.

Ложное объяснение, основанное на равном времени прохождения.

Объяснение «равного времени прохождения» начинается с утверждения, что поток над верхней поверхностью быстрее, чем поток над нижней поверхностью, потому что длина пути над верхней поверхностью больше и его необходимо пройти за равное время прохождения. Принцип Бернулли гласит, что при определенных условиях увеличение скорости потока связано с уменьшением давления. Сделан вывод, что пониженное давление на верхнюю поверхность приводит к подъему вверх.

Хотя это правда, что поток ускоряется, серьезным недостатком этого объяснения является то, что оно не объясняет правильно, что вызывает ускорение потока. Объяснение большей длины пути просто неверно. Никакой разницы в длине пути не требуется, и даже если разница есть, она обычно слишком мала, чтобы объяснить наблюдаемую разницу в скорости. Это связано с тем, что предположение о равном времени прохождения неверно применительно к телу, создающему подъемную силу. Не существует физического принципа, который требовал бы одинакового времени прохождения во всех ситуациях, и результаты экспериментов подтверждают, что для тела, создающего подъемную силу, время прохождения не одинаково. Фактически, воздух, проходящий мимо вершины аэродинамического профиля, создающего подъемную силу, движется намного быстрее, чем предсказывает равное время прохождения. Гораздо более высокая скорость потока над верхней поверхностью хорошо видна на этой анимированной визуализации потока .

Препятствие потоку воздуха

Оптимизация и обтекание труб вокруг аэродинамического профиля, создающего подъемную силу. Поток двумерный, а профиль имеет бесконечный размах. Обратите внимание на более узкие трубки потока вверху и более широкие трубы внизу.

Как и объяснение равного времени прохождения, объяснение «препятствия» или «защемления трубы» утверждает, что поток над верхней поверхностью быстрее, чем поток над нижней поверхностью, но дает другую причину разницы в скорости. В нем утверждается, что изогнутая верхняя поверхность действует как большее препятствие для потока, заставляя линии тока сжиматься ближе друг к другу, делая каналы более узкими. Когда водотоки становятся уже, сохранение массы требует увеличения скорости потока. Пониженное давление на верхней поверхности и подъемная сила следуют из более высокой скорости по принципу Бернулли , как и в объяснении равного времени прохождения. Иногда проводят аналогию с соплом Вентури , утверждая, что верхняя поверхность крыла действует как сопло Вентури, сужая поток.

Одним из серьезных недостатков объяснения препятствий является то, что оно не объясняет, как происходит защемление трубки потока или почему оно сильнее на верхней поверхности, чем на нижней. Для обычных крыльев, плоских снизу и изогнутых сверху, это имеет некоторый интуитивный смысл, но не объясняет, как плоские пластины, симметричные аэродинамические профили, паруса парусника или обычные аэродинамические профили, летящие вверх тормашками, могут создавать подъемную силу, и попытки расчета подъемной силы основаны на на величину сужения или обструкции не предсказывают экспериментальные результаты. Еще один недостаток заключается в том, что сохранение массы не является удовлетворительной физической причиной ускорения потока. Чтобы эффективно объяснить ускорение объекта, необходимо определить силу, которая его ускоряет.

Проблемы, общие для обеих версий объяснения, основанного на Бернулли.

Серьезный недостаток, общий для всех объяснений, основанных на Бернулли, заключается в том, что они подразумевают, что разница скоростей может возникать по причинам, отличным от разницы давления, и что разница скоростей затем приводит к разнице давлений в соответствии с принципом Бернулли. Эта подразумеваемая односторонняя причинно-следственная связь является заблуждением. Настоящая взаимосвязь между давлением и скоростью потока представляет собой взаимное взаимодействие . Как поясняется ниже в разделе с более подробным физическим объяснением , создание подъемной силы требует поддержания разницы давлений как в вертикальном, так и в горизонтальном направлениях. Объяснения Бернулли не объясняют, как сохраняются перепады давления в вертикальном направлении. То есть они исключают часть взаимодействия потока и отклонения.

Хотя два приведенных выше простых объяснения, основанных на Бернулли, неверны, нет ничего неправильного в принципе Бернулли или в том факте, что воздух движется быстрее в верхней части крыла, и принцип Бернулли можно правильно использовать как часть более сложного объяснения подъемной силы. .

Основные атрибуты лифта

Подъемная сила является результатом разницы давлений и зависит от угла атаки, формы профиля, плотности воздуха и скорости полета.

Перепады давления

Давление — это нормальная сила, действующая на единицу площади воздухом на себя и на поверхности, которых он касается. Подъемная сила передается за счет давления, действующего перпендикулярно поверхности профиля. Таким образом, чистая сила проявляется в виде разницы давлений. Направление результирующей силы подразумевает, что среднее давление на верхней поверхности профиля ниже, чем среднее давление на нижней стороне.

Эти перепады давления возникают в связи с искривлением воздушного потока. Когда жидкость движется по изогнутой траектории, существует градиент давления , перпендикулярный направлению потока, с более высоким давлением снаружи кривой и более низким давлением внутри. Эта прямая связь между изогнутыми линиями тока и перепадами давления, иногда называемая теоремой о кривизне линий тока из второго закона Ньютона , была выведена Леонардом Эйлером в 1754 году:

${\frac {\operatorname {d} p}{\operatorname {d} R}}=\rho {\frac {v^{2}}{R}}$

Левая часть этого уравнения представляет собой разницу давлений, перпендикулярную потоку жидкости. В правой части уравнения ρ — плотность, v — скорость, а R — радиус кривизны. Эта формула показывает, что более высокие скорости и более узкая кривизна создают больший перепад давления и что для прямого потока (R → ∞) перепад давления равен нулю.

Угол атаки

Основная статья: Угол атаки

Угол атаки профиля

Угол атаки — это угол между хордой профиля и набегающим потоком воздуха. Симметричный профиль создает нулевую подъемную силу при нулевом угле атаки. Но по мере увеличения угла атаки воздух отклоняется на больший угол, и вертикальная составляющая скорости воздушного потока увеличивается, что приводит к большей подъемной силе. При малых углах симметричный профиль создает подъемную силу, примерно пропорциональную углу атаки.

По мере увеличения угла атаки подъемная сила достигает максимума под некоторым углом; увеличение угла атаки сверх этого критического угла атаки приводит к отделению потока на верхней поверхности от крыла; отклонение вниз меньше, поэтому аэродинамический профиль создает меньшую подъемную силу. Говорят, что аэродинамический профиль заглох .

Форма профиля крыла

Профиль с выпуклостью по сравнению с симметричным профилем.

Максимальная подъемная сила, которую может создать профиль крыла при заданной скорости полета, зависит от формы профиля, особенно от величины изгиба (кривизна, при которой верхняя поверхность более выпуклая, чем нижняя, как показано справа). Увеличение развала обычно увеличивает максимальную подъемную силу при данной скорости полета.

Изогнутые профили создают подъемную силу при нулевом угле атаки. Когда линия хорды горизонтальна, задняя кромка направлена ​​вниз, и, поскольку воздух следует за задней кромкой, он отклоняется вниз. Когда изогнутый профиль перевернут, угол атаки можно отрегулировать так, чтобы подъемная сила была направлена ​​вверх. Это объясняет, как самолет может летать вверх тормашками.

Условия потока

Условия окружающего потока, которые влияют на подъемную силу, включают плотность жидкости, вязкость и скорость потока. На плотность влияет температура и скорость звука среды, т.е. эффекты сжимаемости.

Скорость и плотность воздуха

Подъемная сила пропорциональна плотности воздуха и примерно пропорциональна квадрату скорости потока. Подъемная сила также зависит от размера крыла и обычно пропорциональна площади крыла, проецируемой в направлении подъемной силы. В расчетах удобно измерять подъемную силу с помощью коэффициента подъемной силы, основанного на этих факторах.

Пограничный слой и перетаскивание профиля

Какой бы гладкой ни казалась поверхность аэродинамического профиля, любая поверхность в масштабе молекул воздуха является шероховатой. Молекулы воздуха, летящие на поверхность, отскакивают от шероховатой поверхности в случайных направлениях относительно их первоначальных скоростей. В результате, когда воздух рассматривается как сплошной материал, оказывается, что он не может скользить по поверхности, и скорость воздуха относительно аэродинамического профиля у поверхности уменьшается почти до нуля (т. е. молекулы воздуха «прилипают» к поверхности). к поверхности, а не скользить по ней), то, что известно как условие прилипания . Поскольку скорость воздуха у поверхности близка к нулю, а воздух вдали от поверхности движется, существует тонкий пограничный слой, в котором воздух вблизи поверхности подвергается сдвиговому движению . воздуха Вязкость сопротивляется сдвигу, вызывая напряжение сдвига на поверхности аэродинамического профиля, называемое сопротивлением поверхностного трения . На большей части поверхности большинства аэродинамических профилей пограничный слой естественно турбулентен, что увеличивает сопротивление трения обшивки.

В обычных условиях полета пограничный слой остается прикрепленным как к верхней, так и к нижней поверхностям вплоть до задней кромки, и его влияние на остальную часть потока незначительно. По сравнению с предсказаниями теории невязкого потока , в которой нет пограничного слоя, прикрепленный пограничный слой незначительно уменьшает подъемную силу и несколько изменяет распределение давления, что приводит к связанному с вязкостью сопротивлению давления сверх поверхностного трения. тащить. Сумма сопротивления поверхностного трения и сопротивления давления, связанного с вязкостью, обычно называется сопротивлением профиля .

Остановка

Отрыв воздушного потока от крыла при большом угле атаки

Максимальная подъемная сила профиля при заданной скорости полета ограничена отрывом пограничного слоя . По мере увеличения угла атаки достигается точка, в которой пограничный слой больше не может оставаться прикрепленным к верхней поверхности. Когда пограничный слой отделяется, он оставляет область рециркуляционного потока над верхней поверхностью, как показано на фотографии визуализации потока справа. Это известно как стойло , или сваливание . На углах атаки выше сваливания подъемная сила существенно снижается, но до нуля не падает. Максимальная подъемная сила, которая может быть достигнута до сваливания, с точки зрения коэффициента подъемной силы, как правило, составляет менее 1,5 для одноэлементных профилей и может быть более 3,0 для профилей с щелевыми закрылками высокой подъемной силы и развернутыми передними устройствами.

Блефные тела

Дополнительная информация: Образование вихрей и вибрация, вызванная вихрями.

Обтекание необтекаемых тел – то есть без обтекаемой формы или срывающихся аэродинамических профилей – может также создавать подъемную силу в дополнение к сильной силе сопротивления. Этот подъем может быть постоянным или колебаться из-за образования вихрей . Взаимодействие гибкости объекта с испусканием вихря может усилить эффект колебательной подъемной силы и вызвать вибрации, вызванные вихрем . Например, поток вокруг круглого цилиндра создает вихревую улицу Кармана : вихри сбрасываются поочередно с сторон цилиндра. Колебательный характер потока создает колеблющуюся подъемную силу на цилиндре, хотя чистая (средняя) сила незначительна. подъемной силы Частота характеризуется безразмерным числом Струхаля , которое зависит от числа Рейнольдса потока.

В случае гибкой конструкции эта колебательная подъемная сила может вызвать вихревые вибрации. При определенных условиях – например, при резонансе или сильной корреляции подъемной силы по размаху – результирующее движение конструкции из-за колебаний подъемной силы может быть значительно усилено. Такие вибрации могут создавать проблемы и угрожать обрушением высоких искусственных сооружений, таких как промышленные дымоходы .

В эффекте Магнуса подъемная сила создается вращающимся цилиндром в набегающем потоке. Здесь механическое вращение действует на пограничный слой, заставляя его разделяться в разных местах по обе стороны цилиндра. Асимметричное разделение изменяет эффективную форму цилиндра с точки зрения потока, так что цилиндр действует как подъемный профиль с циркуляцией во внешнем потоке.

Более полное физическое объяснение

Как описано выше в разделе « Упрощенное физическое объяснение подъемной силы на аэродинамическом профиле », существует два основных популярных объяснения: одно основано на отклонении потока вниз (законы Ньютона), а другое — на разнице давлений, сопровождающейся изменениями скорости потока (принцип Бернулли). ). Любой из них сам по себе правильно определяет некоторые аспекты подъемного потока, но оставляет необъясненными другие важные аспекты явления. Более полное объяснение включает как отклонение вниз, так и разницу давлений (включая изменения скорости потока, связанные с разницей давления), и требует более детального рассмотрения потока.

Подъемная сила на поверхности профиля

Форма профиля и угол атаки работают вместе, так что профиль оказывает нисходящую силу на воздух, когда он проходит мимо. Согласно третьему закону Ньютона, воздух должен оказывать на аэродинамический профиль равную и противоположную (направленную вверх) силу, которая и является подъемной силой.

Чистая сила, действующая со стороны воздуха, возникает как разница давлений на поверхностях аэродинамического профиля. Давление в жидкости всегда положительно в абсолютном смысле. поэтому давление всегда следует рассматривать как толкающее, а не как притягивающее. Таким образом, давление оказывает давление на профиль крыла повсюду, как на верхней, так и на нижней поверхности. Текущий воздух реагирует на присутствие крыла, уменьшая давление на верхнюю поверхность крыла и увеличивая давление на нижнюю поверхность. Давление на нижнюю поверхность оказывает большее давление вверх, чем пониженное давление на верхнюю поверхность — вниз, и конечным результатом является подъем вверх.

Разница давлений, вызывающая подъемную силу, действует непосредственно на поверхности профиля; однако понимание того, как создается разница давлений, требует понимания того, что делает поток на более широкой площади.

Более широкий поток вокруг профиля

Обтекание профиля: точки движутся вместе с потоком. Черные точки — это временные срезы , которые разделяются на две части — верхнюю и нижнюю часть — на переднем крае. Заметная разница в скорости между линиями тока верхней и нижней поверхности наиболее четко показана на анимации изображения: верхние маркеры достигают задней кромки задолго до нижних. Цвета точек обозначают линии тока .

Профиль влияет на скорость и направление потока на большой площади, создавая структуру, называемую полем скорости . Когда аэродинамический профиль создает подъемную силу, поток перед аэродинамическим профилем отклоняется вверх, поток над и под аэродинамическим профилем отклоняется вниз, оставляя воздух далеко позади аэродинамического профиля в том же состоянии, что и встречный поток далеко впереди. Поток над верхней поверхностью ускоряется, а поток под профилем замедляется. Вместе с отклонением воздуха вверх спереди и отклонением воздуха вниз непосредственно сзади это создает чистый циркуляционный компонент потока. Отклонение вниз и изменения скорости потока выражены и распространяются на большую площадь, как это видно на анимации потока справа. Эти различия в направлении и скорости потока максимальны вблизи профиля и постепенно уменьшаются далеко вверх и вниз. Все эти особенности поля скорости проявляются и в теоретических моделях подъемных течений.

Давление также подвергается воздействию на обширной территории в виде неоднородного давления, называемого полем давления . Когда профиль создает подъемную силу, над профилем имеется диффузная область низкого давления и обычно диффузная область высокого давления внизу, как показано изобарами (кривыми постоянного давления) на чертеже. Разница давлений, действующая на поверхность, является лишь частью этого поля давления.

Взаимное взаимодействие перепадов давления и изменения скорости потока

Поле давления вокруг профиля. Линии представляют собой изобары одинакового давления по своей длине. Стрелки показывают перепад давления от высокого (красный) до низкого (синий) и, следовательно, также результирующую силу, которая заставляет воздух ускоряться в этом направлении.

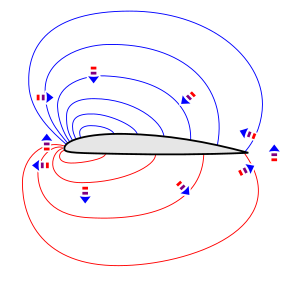
Неравномерное давление оказывает на воздух силы в направлении от более высокого давления к более низкому давлению. Направление силы различно в разных местах аэродинамического профиля, как указано блокирующими стрелками в поле давления вокруг профиля аэродинамического профиля. Воздух над профилем выталкивается к центру области низкого давления, а воздух под крылом выталкивается наружу из центра области высокого давления.

Согласно второму закону Ньютона , сила заставляет воздух ускоряться в направлении силы. Таким образом, вертикальные стрелки на прилагаемой диаграмме поля давления указывают на то, что воздух над и под аэродинамическим профилем ускоряется или поворачивается вниз, и что неравномерное давление, таким образом, является причиной отклонения потока вниз, видимого в анимации потока. Чтобы произвести этот поворот вниз, профиль должен иметь положительный угол атаки или достаточный положительный развал. Обратите внимание, что поворот потока вниз по верхней поверхности является результатом того, что воздух выталкивается вниз под более высоким давлением над ним, чем под ним. Некоторые объяснения, относящиеся к «эффекту Коанды», предполагают, что вязкость играет ключевую роль в развороте вниз, но это неверно. (см. выше в разделе « Споры по поводу эффекта Коанды »).

Стрелки перед аэродинамическим профилем указывают, что поток перед аэродинамическим профилем отклоняется вверх, а стрелки за аэродинамическим профилем указывают, что поток позади аэродинамического профиля снова отклоняется вверх после отклонения вниз по аэродинамическому профилю. Эти отклонения также видны в анимации потока.

Стрелки перед аэродинамическим профилем и позади него также указывают на то, что воздух, проходящий через область низкого давления над аэродинамическим профилем, ускоряется при входе и замедляется при выходе. Воздух, проходящий через область высокого давления под аэродинамическим профилем, замедляется при входе, а затем ускоряется обратно при выходе. Таким образом, неравномерное давление также является причиной изменений скорости потока, видимых на анимации потока. Изменения скорости потока согласуются с принципом Бернулли , который гласит, что при устойчивом потоке без вязкости более низкое давление означает более высокую скорость, а более высокое давление означает более низкую скорость.

Таким образом, изменения направления и скорости потока напрямую вызваны неоднородным давлением. Но эта причинно-следственная связь не просто односторонняя; он работает в обоих направлениях одновременно. На движение воздуха влияет разница давлений, но существование разницы давления зависит от движения воздуха. Таким образом, эта связь представляет собой взаимное или взаимное взаимодействие: поток воздуха меняет скорость или направление в ответ на разницу давления, а разница давления поддерживается сопротивлением воздуха изменению скорости или направления. Разница давлений может существовать только в том случае, если есть что-то, чему она может противостоять. В аэродинамическом потоке разница давлений противодействует инерции воздуха, поскольку воздух ускоряется за счет разницы давлений. Вот почему масса воздуха является частью расчета и почему подъемная сила зависит от плотности воздуха.

Поддержание разницы давлений, которая оказывает подъемную силу на поверхности профиля, требует поддержания неравномерного давления в широкой области вокруг профиля. Это требует поддержания разницы давлений как в вертикальном, так и в горизонтальном направлениях и, таким образом, требует как поворота потока вниз, так и изменения скорости потока в соответствии с принципом Бернулли. Перепады давления и изменения направления и скорости потока поддерживают друг друга во взаимном взаимодействии. Разница давлений естественным образом вытекает из второго закона Ньютона и из того факта, что поток вдоль поверхности повторяет преимущественно наклоненные вниз контуры профиля крыла. И тот факт, что воздух имеет массу, имеет решающее значение для взаимодействия.

Насколько простые объяснения терпят неудачу

Создание подъемной силы требует как поворота потока вниз, так и изменения скорости потока в соответствии с принципом Бернулли. Каждое из упрощенных объяснений, приведенных выше в разделе « Упрощенные физические объяснения подъемной силы на аэродинамическом профиле», терпит неудачу, пытаясь объяснить подъемную силу только с точки зрения одного или другого, таким образом объясняя только часть явления и оставляя другие части необъясненными.

Количественная оценка подъема

Интеграция давления

Когда известно распределение давления на поверхности профиля, для определения общей подъемной силы необходимо сложить вклады в силу давления от локальных элементов поверхности, каждый из которых имеет свое локальное значение давления. Таким образом, общая подъемная сила представляет собой интеграл давления в направлении, перпендикулярном потоку в дальней зоне, на поверхность аэродинамического профиля.

$L=\oint p\mathbf {n} \cdot \mathbf {k} \;\mathrm {d} S,$

где:

• S — площадь проекции (в плане) профиля, измеренная перпендикулярно среднему потоку воздуха;
• n — нормальный единичный вектор, направленный внутрь крыла;
• k — вертикальный единичный вектор, перпендикулярный направлению набегающего потока .

В приведенном выше уравнении подъемной силы не учитываются силы поверхностного трения , которые малы по сравнению с силами давления.

Используя вектор i, параллельный набегающему потоку, вместо k в интеграле, мы получаем выражение для сопротивления давления D _p (которое включает в себя часть давления профиля сопротивления и, если крыло трехмерное, индуцированное сопротивление). тащить). Если мы используем вектор j по размаху , мы получим боковую силу Y .

${\begin{aligned}D_{p}&=\oint p\mathbf {n} \cdot \mathbf {i} \;\mathrm {d} S,\\Y&=\oint p\mathbf {n} \cdot \mathbf {j} \;\mathrm {d} S.\end{aligned}}$

Для достоверности этого интегрирования обычно требуется, чтобы форма профиля крыла представляла собой замкнутую кусочно-гладкую кривую .

Коэффициент подъемной силы

Основная статья: Коэффициент подъемной силы

Подъемная сила зависит от размера крыла и примерно пропорциональна площади крыла. Часто бывает удобно количественно оценить подъемную силу данного профиля по его коэффициенту подъемной силы. $C_{L}$, который определяет его общую подъемную силу, выраженную в единице площади крыла.

Если значение $C_{L}$ для крыла с заданным углом атаки можно определить подъемную силу, создаваемую для конкретных условий потока:

$L={\tfrac {1}{2}}\rho v^{2}SC_{L}$

где

• $L$ это подъемная сила
• $\rho$ плотность воздуха
• $v$ это скорость или истинная воздушная скорость
• $S$ - площадь крыла в плане (проецируемая)
• $C_{L}$ - коэффициент подъемной силы при желаемом угле атаки, число Маха и число Рейнольдса.

Математические теории подъемной силы

Математические теории подъемной силы основаны на механике сплошной жидкости, предполагая, что воздух течет как непрерывная жидкость. Подъемная сила создается в соответствии с фундаментальными принципами физики, наиболее важными из которых являются следующие три принципа:

• Сохранение импульса , которое является следствием законов движения Ньютона , особенно второго закона Ньютона, который связывает результирующую силу, действующую на элемент воздуха, со скоростью изменения его импульса ,
• Сохранение массы , включая предположение, что поверхность профиля непроницаема для обтекающего воздуха, и
• Сохранение энергии , которое гласит, что энергия не создается и не уничтожается.

Поскольку профиль влияет на течение в обширной области вокруг него, законы сохранения механики воплощаются в виде уравнений в частных производных в сочетании с набором требований граничных условий , которым поток должен удовлетворять на поверхности профиля и вдали от него. аэродинамический профиль.

Для прогнозирования подъемной силы требуется решение уравнений для конкретной формы профиля и условий потока, что обычно требует вычислений, которые настолько объемны, что их можно использовать только на компьютере, с помощью методов вычислительной гидродинамики (CFD). Определение чистой аэродинамической силы с помощью решения CFD требует «сложения» ( интегрирования ) сил, возникающих из-за давления и сдвига, определенных с помощью CFD, по каждому элементу поверхности аэродинамического профиля, как описано в разделе « Интеграция давления ».

Уравнения Навье-Стокса (NS) обеспечивают потенциально наиболее точную теорию подъемной силы, но на практике учет эффектов турбулентности в пограничном слое на поверхности профиля требует некоторой точности и требует использования усредненного по Рейнольдсу уравнения Навье-Стокса. уравнения (RANS). Были также разработаны более простые, но менее точные теории.

Уравнения Навье – Стокса (НС)

Эти уравнения представляют собой сохранение массы, второй закон Ньютона (сохранение импульса), сохранение энергии, закон Ньютона для действия вязкости , закон теплопроводности Фурье , уравнение состояния, связывающее плотность, температуру и давление, а также формулы для вязкость и теплопроводность жидкости.

В принципе, уравнения NS в сочетании с граничными условиями отсутствия перетока и скольжения на поверхности профиля могут использоваться для прогнозирования подъемной силы в любой ситуации обычного полета в атмосфере с высокой точностью. Однако в практических ситуациях воздушные потоки всегда связаны с турбулентностью в пограничном слое рядом с поверхностью профиля, по крайней мере, над кормовой частью профиля. Прогнозирование подъемной силы путем решения уравнений NS в их необработанной форме потребует вычислений для разрешения деталей турбулентности, вплоть до мельчайших вихрей. Это пока невозможно даже на самом мощном компьютере. Таким образом, в принципе уравнения NS обеспечивают полную и очень точную теорию подъемной силы, но практическое предсказание подъемной силы требует, чтобы эффекты турбулентности моделировались в уравнениях RANS, а не вычислялись напрямую.

Усредненные по Рейнольдсу уравнения Навье – Стокса (RANS)

Это уравнения NS с турбулентными движениями, усредненными по времени, и эффекты турбулентности на усредненный по времени поток, представленные моделированием турбулентности (дополнительный набор уравнений, основанный на сочетании анализа размерностей и эмпирической информации о том, как турбулентность влияет на поток). пограничный слой в усреднённом по времени смысле). Решение RANS состоит из усредненных по времени вектора скорости, давления, плотности и температуры, определенных в плотной сетке точек, окружающих профиль крыла.

Требуемый объем вычислений составляет ничтожную долю (миллиардные доли). того, что потребуется для разрешения всех турбулентных движений при необработанных расчетах NS, и при наличии больших компьютеров теперь практично выполнять расчеты RANS для целых самолетов в трех измерениях. Поскольку модели турбулентности несовершенны, точность расчетов RANS несовершенна, но достаточна для практического проектирования самолетов. Прогнозируемый RANS подъем обычно находится в пределах нескольких процентов от фактического подъема.

Уравнения невязкого течения (Эйлера или потенциала)

Уравнения Эйлера представляют собой уравнения НШ без учета эффектов вязкости, теплопроводности и турбулентности. Как и решение RANS, решение Эйлера состоит из вектора скорости, давления, плотности и температуры, определенных в плотной сетке точек, окружающих профиль. Хотя уравнения Эйлера проще уравнений НС, они не поддаются точным аналитическим решениям.

Дальнейшее упрощение доступно с помощью теории потенциального потока , которая уменьшает количество неизвестных, которые необходимо определить, и делает возможными аналитические решения в некоторых случаях, как описано ниже.

Расчеты Эйлера или потенциального потока примерно правильно предсказывают распределение давления на поверхностях профиля для углов атаки ниже сваливания, где они могут упустить общую подъемную силу на целых 10–20%. При углах атаки выше сваливания невязкие расчеты не предсказывают, что сваливание произошло, и в результате они сильно переоценивают подъемную силу.

В теории потенциального потока предполагается, что поток является безвихревым , то есть небольшие порции жидкости не имеют чистой скорости вращения. Математически это выражается утверждением, что ротор векторного поля скорости всюду равен нулю. Безвихревые потоки обладают тем удобным свойством, что скорость можно выразить как градиент скалярной функции, называемой потенциалом . Поток, представленный таким образом, называется потенциальным потоком.

В теории потенциального потока поток считается несжимаемым. Преимущество теории несжимаемого потенциального потока состоит в том, что уравнение ( уравнение Лапласа ), которое необходимо решить для потенциала, является линейным , что позволяет строить решения путем суперпозиции других известных решений. Уравнение потока несжимаемой жидкости также можно решить с помощью конформного отображения — метода, основанного на теории функций комплексной переменной. В начале 20-го века, до того, как стали доступны компьютеры, конформное отображение использовалось для генерации решений уравнения потенциального потока несжимаемой жидкости для класса идеализированных форм профиля крыла, что дало некоторые из первых практических теоретических предсказаний распределения давления на поднимающемся профиле крыла.

Решение потенциального уравнения непосредственно определяет только поле скорости. Поле давления выводится из поля скорости с помощью уравнения Бернулли.

Сравнение неподъемной картины обтекания профиля; и характер подъемного потока, соответствующий условию Кутты, при котором поток плавно покидает заднюю кромку.

Применение теории потенциального потока к подъемному потоку требует специального подхода и дополнительных предположений. Проблема возникает потому, что подъемная сила на профиле в невязком потоке требует циркуляции в потоке вокруг профиля (см. « Циркуляция и теорема Кутты-Жуковского » ниже), но единственная потенциальная функция, непрерывная во всей области вокруг профиля, не может представлять собой поток с ненулевой циркуляцией. Решение этой проблемы состоит в том, чтобы ввести разрез ветки , кривую или линию от некоторой точки поверхности профиля на бесконечное расстояние и допустить скачок значения потенциала поперек разреза. Скачок потенциала вызывает циркуляцию в потоке, равную скачку потенциала, и, таким образом, позволяет представить ненулевую циркуляцию. Однако скачок потенциала является свободным параметром, который не определяется уравнением потенциала или другими граничными условиями, поэтому решение является неопределенным. Решение потенциального потока существует для любого значения циркуляции и любого значения подъемной силы. Один из способов разрешить эту неопределенность — ввести Состояние Кутты , а именно, из всех возможных решений физически разумным является то, при котором поток плавно покидает заднюю кромку. Эскизы линий тока иллюстрируют одну картину течения с нулевой подъемной силой, при которой поток огибает заднюю кромку и покидает верхнюю поверхность перед задней кромкой, и другую схему течения с положительной подъемной силой, при которой поток плавно уходит у задней кромки в соответствии с условием Кутты.

Линеаризованный потенциальный поток

Это теория потенциального потока с дальнейшими предположениями, что профиль очень тонкий, а угол атаки мал. Линеаризованная теория предсказывает общий характер распределения давления на профиле и то, как на него влияют форма профиля и угол атаки, но недостаточно точна для проектных работ. Для 2D-профиля такие расчеты можно выполнить за доли секунды в электронной таблице на ПК.

Циркуляция и теорема Кутты – Жуковского

Циркуляционная составляющая обтекания профиля

Когда профиль создает подъемную силу, несколько компонентов общего поля скоростей способствуют чистой циркуляции воздуха вокруг него: восходящий поток перед профилем, ускоренный поток вверху, замедленный поток внизу и нисходящий поток позади.

Циркуляцию можно понимать как общую величину «вращения» (или завихрения ) невязкой жидкости вокруг аэродинамического профиля.

Теорема Кутты-Жуковского связывает подъемную силу на единицу ширины размаха двумерного профиля с этой циркуляционной составляющей потока. Это ключевой элемент в объяснении подъемной силы, которая следует за развитием потока вокруг профиля, когда профиль начинает свое движение из состояния покоя, а стартовый вихрь образуется и остается позади, что приводит к образованию циркуляции вокруг профиля. Затем подъемная сила выводится из теоремы Кутты-Жуковского. Это объяснение в значительной степени математическое, и его общее развитие основано на логических выводах, а не на физических причинах и следствиях.

Модель Кутты-Жуковского не предсказывает, какую циркуляцию или подъемную силу создает двумерный профиль крыла. Для расчета подъемной силы на единицу пролета с использованием Кутты – Жуковского требуется известное значение циркуляции. В частности, если выполняется условие Кутты, при котором задняя критическая точка перемещается к задней кромке профиля и закрепляется там на время полета, подъемная сила может быть рассчитана теоретически с помощью метода конформного отображения.

Подъемная сила, создаваемая обычным профилем, определяется как его конструкцией, так и условиями полета, такими как скорость движения вперед, угол атаки и плотность воздуха. Подъемную силу можно увеличить путем искусственного увеличения циркуляции, например, путем выдувания пограничного слоя или использования выдувных закрылков . В роторе Флеттнера весь профиль имеет круглую форму и вращается вокруг оси размаха, создавая циркуляцию.

Трехмерный поток

Поперечное сечение комбинации крыло-корпус самолета, показывающее изобары трехмерного подъемного потока.

Поперечное сечение комбинации крыло-корпус самолета, показывающее векторы скорости трехмерного подъемного потока.

Обтекание трехмерного крыла сопряжено со значительными дополнительными проблемами, особенно касающимися законцовок крыла. Для крыла с малым удлинением , такого как типичное треугольное крыло , двумерные теории могут обеспечить плохую модель, а эффекты трехмерного потока могут доминировать. Даже для крыльев с большим удлинением трехмерные эффекты, связанные с конечным размахом, могут влиять на весь размах, а не только вблизи законцовок.

Законцовки крыла и распределение по размаху

Вертикальный градиент давления на законцовках крыла заставляет воздух течь вбок, из-под крыла, затем вверх и обратно по верхней поверхности. Это уменьшает градиент давления на законцовке крыла, а следовательно, и подъемную силу. Подъемная сила имеет тенденцию уменьшаться в направлении размаха от основания к законцовке, и распределение давления вокруг секций профиля соответственно изменяется в направлении размаха. Распределение давления в плоскостях, перпендикулярных направлению полета, имеет тенденцию выглядеть так, как показано на рисунке справа. Такое изменяющееся по размаху распределение давления поддерживается за счет взаимного взаимодействия с полем скорости. Поток под крылом ускоряется снаружи, поток за пределами законцовок ускоряется вверх, а поток над крылом ускоряется внутрь, что приводит к схеме потока, показанной справа.

Поток поворачивается вниз сильнее, чем был бы в двумерном потоке с той же формой профиля и подъемной силой в сечении, а для достижения той же подъемной силы требуется более высокий угол атаки в сечении по сравнению с двумерным потоком. Крыло фактически летит с нисходящим потоком, созданным им самим, как если бы набегающий поток был наклонен вниз, в результате чего общий вектор аэродинамической силы немного наклонен назад по сравнению с тем, что было бы в двух измерениях. Дополнительная обратная составляющая вектора силы называется сопротивлением, вызванным подъемной силой .

Вычисление Эйлера концевого вихря, скатывающегося из прицепного листа завихренности

Разница в составляющей скорости по размаху над и под крылом (между внутренним направлением вверху и внешним направлением внизу) сохраняется на задней кромке и в следе вниз по течению. После того, как поток покидает заднюю кромку, эта разница в скорости возникает в относительно тонком слое сдвига, называемом вихревой пеленой.

Подковообразная вихревая система

Вид сверху на крыло, показывающий подковообразную вихревую систему.

Поток на законцовках крыла, выходящий из крыла, создает вихрь на законцовке. Когда основной вихревой лист проходит вниз по потоку от задней кромки, он сворачивается на своих внешних краях, сливаясь с вершинными вихрями. Совокупность вихрей на законцовках крыла и питающих их вихревых листов называется вихревым следом.

Помимо завихренности в следящем вихревом следе существует завихренность в пограничном слое крыла, называемая «связанной завихренностью», которая соединяет отстающие листы с двух сторон крыла в вихревую систему общей формы подковы. Подковообразная форма вихревой системы была признана британским пионером воздухоплавания Ланчестером в 1907 году.

Учитывая распределение связанной завихренности и завихренности в следе, закон Био – Савара (соотношение векторного исчисления) можно использовать для расчета возмущения скорости в любой точке поля, вызванного подъемной силой крыла. Приближенные теории распределения подъемной силы и сопротивления трехмерных крыльев, вызванного подъемной силой, основаны на таком анализе, примененном к подковообразной вихревой системе крыла. В этих теориях связанная завихренность обычно идеализируется и предполагается, что она находится на поверхности изгиба внутри крыла.

Поскольку в таких теориях скорость выводится из завихренности, некоторые авторы описывают ситуацию, подразумевая, что завихренность является причиной возмущений скорости, используя, например, такие термины, как «скорость, индуцированная вихрем». Но такое объяснение механической причинно-следственной связи между завихренностью и скоростью не согласуется с физикой. Возмущения скорости при обтекании крыла фактически создаются полем давления.

Проявления подъема в дальнем поле

Комплексный баланс силы/импульса в подъемных потоках

Контрольные объемы различной формы, которые использовались при анализе баланса импульса в двумерном обтекании несущего профиля. Предполагается, что профиль оказывает на воздух нисходящую силу -L' на единицу пролета, и пропорции, в которых эта сила проявляется в виде потоков импульса и разницы давлений на внешней границе, указаны для каждой различной формы контрольного объема.

Обтекание несущего профиля должно удовлетворять второму закону Ньютона о сохранении импульса как локально в каждой точке поля потока, так и в интегральном смысле в любой протяженной области потока. Для расширенной области второй закон Ньютона принимает форму теоремы об импульсе для контрольного объема , где контрольным объемом может быть любая область потока, выбранная для анализа. Теорема об импульсе утверждает, что интегрированная сила, действующая на границах контрольного объема ( поверхностный интеграл ), равна интегрированной скорости изменения времени ( материальная производная ) импульса частиц жидкости, проходящих через внутреннюю часть контрольного объема. Для установившегося течения это можно выразить в виде чистого поверхностного интеграла потока импульса через границу.

Подъемный поток вокруг двумерного профиля обычно анализируется в контрольном объеме, который полностью окружает профиль, так что внутренней границей контрольного объема является поверхность профиля, где нисходящая сила на единицу размаха $-L'$ действует на жидкость со стороны аэродинамического профиля. Внешняя граница обычно представляет собой большой круг или большой прямоугольник. На этой внешней границе, удаленной от профиля, скорость и давление хорошо представлены скоростью и давлением, связанными с однородным потоком плюс вихрь, а вязкое напряжение незначительно, так что единственная сила, которая должна быть интегрирована по внешней границе, равна давление. Скорость набегающего потока обычно предполагается горизонтальной с подъемной силой вертикально вверх, так что интересующим компонентом является вертикальный импульс.

Для случая свободного воздуха (без заземляющего слоя) сила $-L'$ Воздействие профиля на жидкость частично проявляется в виде потоков импульса, а частично в виде перепадов давления на внешней границе в пропорциях, которые зависят от формы внешней границы, как показано на диаграмме справа. Для плоского горизонтального прямоугольника, длина которого намного превышает его высоту, потоки вертикального импульса через переднюю и заднюю часть пренебрежимо малы, а подъемная сила полностью объясняется совокупной разностью давлений сверху и снизу. Для квадрата или круга потоки импульса и разности давлений составляют половину подъемной силы каждый. Для вертикального прямоугольника, высота которого значительно превышает его ширину, неуравновешенные силы давления сверху и снизу незначительны, а подъемная сила полностью объясняется потоками импульса, причем поток восходящего импульса поступает в управляющий объем через передний учет. половину подъемной силы, а поток нисходящего импульса, который выходит из контрольного объема через заднюю часть, составляет другую половину.

Результаты всех описанных выше анализов контрольного объема согласуются с описанной выше теоремой Кутты-Жуковского. При выводе теоремы использовались контрольные объемы как высокого прямоугольника, так и круга.

Подъемная сила среагировала избыточным давлением на землю под самолетом.

Иллюстрация распределения давления выше атмосферного на земле под самолетом в дозвуковом полете

Профиль создает поле давления в окружающем воздухе, как описано выше в разделе « Более широкое обтекание профиля ». Связанные с этим полем перепады давления постепенно затухают, становясь очень малыми на больших расстояниях, но никогда не исчезая совсем. Под самолетом поле давления сохраняется в виде положительного возмущения давления, которое достигает земли, образуя на земле картину давления, немного превышающего окружающее, как показано справа. Хотя разница давлений очень мала далеко под самолетом, она распространяется на большую площадь и в сумме образует значительную силу. При устойчивом горизонтальном полете суммарная сила, возникающая из-за разницы давлений, равна общей аэродинамической подъемной силе самолета и весу самолета. Согласно третьему закону Ньютона, этой силе давления, действующей на землю со стороны воздуха, соответствует равная и противоположная направленная вверх сила, действующая на воздух со стороны земли, которая компенсирует всю нисходящую силу, действующую на воздух со стороны самолета. Таким образом, чистая сила подъемной силы, действующая на атмосферу в целом, равна нулю, и, следовательно, в атмосфере не происходит комплексного накопления вертикального импульса, как было отмечено Ланчестером на ранних этапах развития современной аэродинамики.

См. также

• Коэффициент сопротивления
• Разделение потока
• Гидродинамика
• Фольга (механика жидкости)
• Эффект Кюсснера
• Отношение подъемной силы к лобовому сопротивлению
• Теория подъемной линии
• Спойлер (автомобильный)

Ссылки

• Эбботт, Айдахо; фон Дёнхофф, AE (1958), Теория секций крыла , Dover Publications
• Андерсон, DF; Эберхардт, С. (2001), Понимание полета , McGraw-Hill.
• Андерсон, JD (1991), Основы аэродинамики, 2-е изд. , МакГроу-Хилл
• Андерсон, JD (1995), Вычислительная гидродинамика, Основы с приложениями , ISBN  978-0-07-113210-7
• Андерсон, доктор юридических наук (1997), История аэродинамики , издательство Кембриджского университета.
• Андерсон, JD (2004), Введение в полет (5-е изд.), McGraw-Hill, стр. 352–361, §5.19, ISBN  978-0-07-282569-5
• Андерсон, доктор юридических наук (2008), «Введение в полет», 6-е издание , McGraw Hill
• Арис, Р. (1989), Векторы, тензоры и основные уравнения механики жидкости , Dover Publications.
• Ауэрбах, Д. (2000), «Почему самолеты летают», Eur. Дж. Физ. , 21 (4): 289–296, Бибкод : 2000EJPh...21..289A , doi : 10.1088/0143-0807/21/4/302 , S2CID   250821727
• Бабинский, Х. (2003), «Как работают крылья?», Phys. Образование. , 38 (6): 497, Bibcode : 2003PhyEd..38..497B , doi : 10.1088/0031-9120/38/6/001 , S2CID   1657792
• Бэтчелор, Г.К. (1967), Введение в гидродинамику , издательство Кембриджского университета.
• Клэнси, LJ (1975), Аэродинамика , Научно-технический институт Лонгмана
• Крейг, генеральный директор (1997), Прекратите злоупотреблять Бернулли , Андерсон, Индиана: Регенеративная пресса
• Дюран, В.Ф., изд. (1932), Аэродинамическая теория, вып. 1 , Дуврские публикации
• Истлейк, Китай (2002), «Взгляд аэродинамики на подъемную силу, Бернулли и Ньютон», Учитель физики , 40 (3): 166–173, Бибкод : 2002PhTea..40..166E , doi : 10.1119/1.1466553 , S2CID   121425815
• Джинс, Дж. (1967), Введение в кинетическую теорию газов , издательство Кембриджского университета.
• Кулфан, Б.М. (2010), Палеоаэродинамические исследования, часть I: Эволюция биологических и технических полетов , AIAA 2010-154.
• Ланчестер, Ф.В. (1907), Аэродинамика , А. Констебль и Ко.
• Лангевише, В. (1944), Палка и руль направления - объяснение искусства полета , McGraw-Hill
• Лиссаман, PBS (1996), Факты подъема , AIAA 1996–161.
• Марчай, Калифорния (1985), Теория и практика парусного спорта , Патнэм
• Макбит, С. (2006), Аэродинамика гоночных автомобилей , Спаркфорд, Хейнс
• Маклин, Д. (2012), Понимание аэродинамики – аргументация из реальной физики , Уайли
• Милн-Томсон, LM (1966), Теоретическая аэродинамика, 4-е изд. , Дуврские публикации
• Прандтль, Л.; Титдженс, О.Г. (1934), Прикладная гидро- и аэромеханика , Dover Publications.
• Раскин, Дж. (1994), Эффект Коанды: понимание того, почему работают крылья , заархивировано из оригинала 28 сентября 2007 г.
• Шлихтинг, Х. (1979), Теория пограничного слоя, седьмое изд. , МакГроу-Хилл
• Шапиро, А.Х. (1953), Динамика и термодинамика потока сжимаемой жидкости , Ronald Press Co.
• Смит, Н.Ф. (1972), «Бернулли и Ньютон в механике жидкости», Учитель физики , 10 (8): 451, Бибкод : 1972PhTea..10..451S , doi : 10.1119/1.2352317
• Спаларт, Филипп Р. (2000), Стратегии моделирования и моделирования турбулентности , том. 21, Международный журнал по теплу и потоку жидкости, стр. 21. 252
• Шумер, Б.; Мутлу; Фредсё, Йорген (2006), Гидродинамика цилиндрических конструкций (переработанная ред.) {{citation}}: CS1 maint: несколько имен: список авторов ( ссылка )
• Туэйтс, Б., изд. (1958), Аэродинамика несжимаемой жидкости , Dover Publications
• Триттон, ди-джей (1980), Физическая гидродинамика , Ван Ностранд Рейнхольд
• Ван Дайк, М. (1969), «Теория пограничного слоя высшего порядка», Annual Review of Fluid Mechanics , 1 (1): 265–292, Бибкод : 1969AnRFM...1..265D , doi : 10.1146/annurev .fl.01.010169.001405
• фон Мизес, Р. (1959), Теория полета , Dover Publications
• Уолтем, К. (1998), «Полет без Бернулли», Учитель физики , 36 (8): 457–462, Бибкод : 1998PhTea..36..457W , doi : 10.1119/1.879927
• Вельтнер, К. (1987), «Сравнение объяснений аэродинамической подъемной силы», Am. Дж. Физ. , 55 (1): 53, Бибкод : 1987AmJPh..55...50W , doi : 10.1119/1.14960
• Уайт, FM (1991), Поток вязкой жидкости, 2-е изд. , МакГроу-Хилл
• Вилле, Р.; Фернхольц, Х. (1965), «Отчет о первом европейском коллоквиуме по механике по эффекту Коанда», J. Fluid Mech. , 23 (4): 801–819, Бибкод : 1965JFM....23..801W , doi : 10.1017/s0022112065001702 , S2CID   121981660
• Уильямсон, ЧК; Говардхан, Р. (2004), «Вихревые вибрации», Annual Review of Fluid Mechanics , 36 : 413–455, Bibcode : 2004AnRFM..36..413W , doi : 10.1146/annurev.fluid.36.050802.122128 , S2CID   58937745
• Здравкович, М.М. (2003), Обтекание круглых цилиндров 2 , Oxford University Press, стр. 850–855, ISBN  978-0-19-856561-1

Дальнейшее чтение

• «Введение в полет» , Джон Д. Андерсон-младший, МакГроу-Хилл, ISBN   0-07-299071-6 - Доктор Андерсон является куратором отдела аэродинамики Национального музея авиации и космонавтики Смитсоновского института и почетным профессором Университета Мэриленда.
• «Понимание полета» , Дэвид Андерсон и Скотт Эберхардт, McGraw-Hill, ISBN   0-07-136377-7 - Физик и авиационный инженер объясняют полет нетехническими терминами и конкретно обращаются к мифу о равном времени полета. Они связывают циркуляцию профиля с эффектом Коанда, что является спорным.
• Аэродинамика , Клэнси, LJ (1975), раздел 4.8, Pitman Publishing Limited, Лондон. ISBN   0-273-01120-0 .
• Аэродинамика, аэронавтика и механика полета , Маккормик, Барнс В., (1979), глава 3, John Wiley & Sons, Inc., Нью-Йорк ISBN   0-471-03032-5 .
• Основы полета , Ричард С. Шевелл, Prentice-Hall International Editions, ISBN   0-13-332917-8 – это текст для односеместрового курса бакалавриата по машиностроению или авиационной технике. Его разделы, посвященные теории полета, понятны при поверхностном знании математического анализа и физики.
• Крейг, Пол П. (1957). «Наблюдение идеального потенциального потока в сверхтекучей жидкости». Физический обзор . 108 (5): 1109–1112. Бибкод : 1957PhRv..108.1109C . дои : 10.1103/PhysRev.108.1109 . – Эксперименты в условиях сверхтекучести , приводящие к исчезновению подъемной силы в невязком потоке, поскольку условие Кутты больше не выполняется.
• «Аэродинамика на уровне частиц», Чарльз А. Краммер (2005 г., редакция 2012 г.) - трактовка аэродинамики, подчеркивающая корпускулярную природу воздуха, в отличие от обычно используемого жидкостного приближения. arXiv : nlin/0507032
• «Полет без Бернулли» Крис Уолтем Том. 36 ноября 1998 г. Учитель физики - используя физическую модель, основанную на втором законе Ньютона, автор представляет строгую гидродинамическую модель полета. [8] Архивировано 28 сентября 2011 г. в Wayback Machine.
• Бернулли, Ньютон и динамический подъем. Норман Ф. Смит. Школьная наука и математика, том 73. Часть I: Бернулли, Ньютон и динамический подъем. Часть II * Архивировано 17 декабря 2012 г., в archive.today. Часть II Бернулли, Ньютон и динамический подъем. Часть II. I * Архивировано 14 декабря 2017 г. в Wayback Machine.

Внешние ссылки

• Обсуждение очевидного «конфликта» между различными объяснениями лифта. Архивировано 25 июля 2021 года в Wayback Machine.
• Учебное пособие НАСА с анимацией, описывающее подъемную силу. Архивировано 9 марта 2009 г. в Wayback Machine.
• NASA FoilSim II 1.5 бета. Симулятор лифта
• Объяснение подъемной силы с анимацией потока жидкости вокруг аэродинамического профиля. Архивировано 13 июня 2021 г. в Wayback Machine.
• Объяснение того, почему и как крылья создают подъемную силу, основанную на давлении. Архивировано 19 декабря 2006 г. в Wayback Machine.
• Физика полета – обзор. Архивировано 9 марта 2021 г. на Wayback Machine . Интернет-доклад профессора доктора Клауса Вельтнера
• Как работают крылья? Хольгер Бабинский
• Бернулли или Ньютон: кто прав насчет подъемной силы? Архивировано 24 сентября 2015 года в Wayback Machine Plane and Pilot . журнале
• Физика за одну минуту. Как на самом деле работает крыло? Архивировано 20 мая 2021 г. в Wayback Machine (видео на YouTube).
• Как на самом деле работают крылья, Кембриджский университет. Архивировано 14 июня 2021 года, в Wayback Machine Хольгера Бабинского (со ссылкой на видео на YouTube «Одна минута физики: как на самом деле работает крыло?»)
• От вершины до морского дна – поднимаемый вес как функция высоты и глубины, Рольф Штайнеггер
• Интерактивное веб-приложение Joukowski Transform. Архивировано 19 октября 2019 г. в Wayback Machine.
• Как летают самолеты. Архивировано 11 июня 2021 года на YouTube-презентации Wayback Machine Кшиштофа Фидковского, доцента кафедры аэрокосмической техники Мичиганского университета.