Классическая проблема центральной силы

В классической механике задача центральной силы заключается в определении движения частицы в одном центральном потенциальном поле . Центральная сила — это сила (возможно, отрицательная), которая направлена ​​от частицы непосредственно к фиксированной точке пространства, центру, и величина которой зависит только от расстояния объекта до центра. В некоторых важных случаях проблема может быть решена аналитически, т. е. с использованием хорошо изученных функций, таких как тригонометрические функции .

Решение этой проблемы важно для классической механики , поскольку многие природные силы являются центральными. Примеры включают гравитацию и электромагнетизм, описываемые законом всемирного тяготения Ньютона и законом Кулона соответственно. Эта проблема важна еще и потому, что некоторые более сложные задачи классической физики (например, задача двух тел с силами, действующими вдоль линии, соединяющей два тела) можно свести к задаче о центральной силе. Наконец, решение проблемы центральной силы часто дает хорошее начальное приближение к истинному движению, как, например, при расчете движения планет в Солнечной системе .

Основы

Суть задачи центральной силы состоит в том, чтобы найти положение r частицы, движущейся под действием центральной силы F , либо в зависимости от времени t , либо в зависимости от угла φ относительно центра силы и произвольной оси.

Определение центральной силы

Центральная сила притяжения, действующая на тело в положении P (показано красным). По определению, центральная сила должна быть направлена ​​либо к фиксированной точке O (если она притягивает), либо от нее (если отталкивает).

Смотрите также: Центральная сила и обозначения Ньютона.

Консервативная центральная сила F имеет два определяющих свойства. Во-первых, он должен направлять частицы либо прямо к фиксированной точке пространства, центру силы, который часто обозначают О, либо от него . Другими словами, центральная сила должна действовать вдоль линии, соединяющей О с текущим положением частицы. Во-вторых, консервативная центральная сила зависит только от расстояния r между О и движущейся частицей; оно не зависит явно от времени или других дескрипторов положения.

Это двойное определение может быть выражено математически следующим образом. Центр силы О можно выбрать в качестве начала системы координат. Вектор r, соединяющий O с текущим положением частицы, известен как вектор положения . Следовательно, центральная сила должна иметь математическую форму $$\mathbf {F} =F(r){\hat {\mathbf {r} }}$$где r — величина вектора | р | (расстояние до центра силы), а r̂ = r /r — соответствующий единичный вектор . Согласно второму закону движения Ньютона , центральная сила F создает параллельное ускорение a, масштабируемое массой m частицы. $$\mathbf {F} =F(r){\hat {\mathbf {r} }}=m\mathbf {a} =m{\ddot {\mathbf {r} }}$$

Для сил притяжения F ( r ) отрицательна, поскольку она уменьшает расстояние r до центра. И наоборот, для сил отталкивания F ( r ) положительна.

Потенциальная энергия

Смотрите также: Кинетическая энергия и Потенциальная энергия.

Если центральная сила является консервативной силой , то величину F ( r ) центральной силы всегда можно выразить как производную независимой от времени потенциальной энергии функции U ( r ) $$F(r)=-{\frac {dU}{dr}}$$

Таким образом, полная энергия частицы — сумма ее кинетической энергии и потенциальной энергии U — является константой; Говорят, что энергия сохраняется . Чтобы показать это, достаточно того, что работа W, совершаемая силой, зависит только от начального и конечного положений, а не от пути, пройденного между ними.

$$W=\int _{\mathbf {r} _{1}}^{\mathbf {r} _{2}}\mathbf {F} \cdot d\mathbf {r} =\int _{\mathbf {r} _{1}}^{\mathbf {r} _{2}}F(r){\hat {\mathbf {r} }}\cdot d\mathbf {r} =\int _{r_{1}}^{r_{2}}Fdr=U(r_{1})-U(r_{2})$$

Эквивалентно, достаточно, чтобы ротор силового поля F был равен нулю; используя формулу ротора в сферических координатах , $$\nabla \times \mathbf {F} ={\frac {1}{r\sin \theta }}\left({\frac {\partial F}{\partial \varphi }}\right){\hat {\boldsymbol {\theta }}}-{\frac {1}{r}}\left({\frac {\partial F}{\partial \theta }}\right){\hat {\boldsymbol {\varphi }}}=0$$потому что частные производные для центральной силы равны нулю; величина F не зависит от угловых сферических координат θ и φ.

Поскольку скалярный потенциал V ( r ) зависит только от расстояния r до начала координат, он обладает сферической симметрией . В этом отношении проблема центральной силы аналогична геодезическим Шварцшильда в общей теории относительности и квантовомеханическим трактовкам частиц в потенциалах сферической симметрии .

Одномерная проблема

Если начальная скорость v частицы совпадает с вектором положения r , то движение всегда остается на линии, определяемой r . Это следует из того, что сила – а согласно второму закону Ньютона, также и ускорение a – также ориентирована на r . Для определения этого движения достаточно решить уравнение $$m{\ddot {r}}=F(r)$$

Одним из методов решения является использование закона сохранения полной энергии. $$|{\dot {r}}|={\Big |}{\frac {dr}{dt}}{\Big |}={\sqrt {\frac {2}{m}}}{\sqrt {E_{\text{tot}}-U(r)}}$$

Беря обратное и интегрируя, получаем: $$|t-t_{0}|={\sqrt {\frac {m}{2}}}\int {\frac {|dr|}{\sqrt {E_{\text{tot}}-U(r)}}}$$

В оставшейся части статьи предполагается, что начальная скорость v частицы не совпадает с вектором положения r , т. е. что углового момента вектор L = r × m v не равен нулю.

Равномерное круговое движение

Любая центральная сила может производить равномерное круговое движение при условии, что начальный радиус r и скорость v удовлетворяют уравнению для центростремительной силы. $${\frac {mv^{2}}{r}}=F(r)$$

Если это уравнение удовлетворяется в начальные моменты, оно будет выполняться и во все последующие моменты времени; частица будет продолжать двигаться по кругу радиуса r со скоростью v вечно.

Связь с классической задачей двух тел

Положения x ₁ и x ₂ двух тел можно выразить через их относительное расстояние r и положение их центра масс R _cm .

Основная статья: Задача двух тел

Проблема центральной силы касается идеальной ситуации («проблемы одного тела»), в которой отдельная частица притягивается или отталкивается от неподвижной точки O , центра силы. Однако физические силы обычно действуют между двумя телами; и согласно третьему закону Ньютона, если первое тело прикладывает силу ко второму, второе тело прикладывает равную и противоположную силу к первому. Следовательно, оба тела ускоряются, если между ними присутствует сила; не существует совершенно неподвижного центра силы. Однако если одно тело значительно массивнее другого, его ускорением относительно другого можно пренебречь; центр более массивного тела можно считать приблизительно фиксированным. Например, Солнце значительно массивнее планеты Меркурий; следовательно, Солнце можно представить как неподвижный центр силы, сводя проблему к движению Меркурия в ответ на силу, приложенную Солнцем. В действительности, однако, Солнце тоже движется (хотя и незначительно) в ответ на силу, приложенную планетой Меркурий.

Любая классическая задача двух тел должна быть преобразована в эквивалентную задачу одного тела. Масса ц одного эквивалентного тела равна приведенной массе двух исходных тел, а ее положение г равно разности их положений.

Однако в таких приближениях нет необходимости. Законы движения Ньютона позволяют преобразовать любую классическую задачу двух тел в соответствующую точную задачу одного тела. Чтобы продемонстрировать это, пусть x ₁ и x ₂ будут положениями двух частиц, а r = x ₁ − x ₂ будет их относительным положением. Тогда по второму закону Ньютона $${\ddot {\mathbf {r} }}={\ddot {\mathbf {x} }}_{1}-{\ddot {\mathbf {x} }}_{2}=\left({\frac {\mathbf {F} _{21}}{m_{1}}}-{\frac {\mathbf {F} _{12}}{m_{2}}}\right)=\left({\frac {1}{m_{1}}}+{\frac {1}{m_{2}}}\right)\mathbf {F} _{21}$$

Окончательное уравнение выводится из третьего закона Ньютона ; сила второго тела на первое тело ( F ₂₁ ) равна и противоположна силе первого тела на второе ( F ₁₂ ). Таким образом, уравнение движения для r можно записать в виде $$\mu {\ddot {\mathbf {r} }}=\mathbf {F}$$где $\mu$ это приведенная масса $$\mu ={\frac {1}{{\frac {1}{m_{1}}}+{\frac {1}{m_{2}}}}}={\frac {m_{1}m_{2}}{m_{1}+m_{2}}}$$

В частном случае задача двух тел, взаимодействующих под действием центральной силы, может быть сведена к задаче о центральной силе одного тела.

Качественные свойства

Плоское движение

Иллюстрация плоского движения. Вектор углового момента L постоянен; следовательно, вектор положения r и вектор скорости v должны лежать в желтой плоскости, перпендикулярной L .

Смотрите также: Угловой момент

Движение частицы под действием центральной силы F всегда остается в плоскости, определяемой ее начальным положением и скоростью. Это можно увидеть по симметрии. Поскольку положение r , скорость v и сила F лежат в одной плоскости, никогда не существует ускорения, перпендикулярного этой плоскости, потому что это нарушит симметрию между «над» плоскостью и «ниже» плоскости.

Чтобы продемонстрировать это математически, достаточно показать, что момент импульса частицы постоянен. Этот угловой момент L определяется уравнением $$\mathbf {L} =\mathbf {r} \times \mathbf {p} =\mathbf {r} \times m\mathbf {v}$$где m — масса частицы, а p — ее линейный импульс . В этом уравнении символ времени × указывает векторное векторное произведение , а не умножение. Следовательно, вектор углового момента L всегда перпендикулярен плоскости, определяемой вектором положения частицы r и вектором скорости v .

В общем, скорость изменения углового момента L равна чистому крутящему моменту r × F. $${\frac {d\mathbf {L} }{dt}}={\dot {\mathbf {r} }}\times m\mathbf {v} +\mathbf {r} \times m{\dot {\mathbf {v} }}=\mathbf {v} \times m\mathbf {v} +\mathbf {r} \times \mathbf {F} =\mathbf {r} \times \mathbf {F} \ ,$$

Первый член m v × v всегда равен нулю, потому что векторное произведение всегда равно нулю для любых двух векторов, указывающих в одном или противоположных направлениях. Однако, когда F является центральной силой, оставшийся член r × F также равен нулю, поскольку векторы r и F направлены в одном или противоположных направлениях. Следовательно, вектор углового момента L постоянен. Затем $$\mathbf {r} \cdot \mathbf {L} =\mathbf {r} \cdot (\mathbf {r} \times \mathbf {p} )=\mathbf {p} \cdot (\mathbf {r} \times \mathbf {r} )=0$$

Следовательно, положение частицы r (а значит, и скорость v ) всегда лежит в плоскости, L. перпендикулярной

Полярные координаты

Вектор положения r точки P на плоскости можно определить по ее расстоянию r от центра (начала координат O ) и ее азимутальному углу φ . Декартовы компоненты x и y вектора равны r cos φ и r sin φ соответственно.

См. Также: Полярная система координат.

Поскольку движение плоское, а сила радиальная, принято переходить к полярным координатам . В этих координатах вектор положения r представлен через радиальное расстояние r и азимутальный угол φ .

$$\mathbf {r} =(x,\ y)=r(\cos \varphi ,\ \sin \varphi )$$

Взяв первую производную по времени, получим вектор скорости частицы v. $$\mathbf {v} ={\frac {d\mathbf {r} }{dt}}={\dot {r}}(\cos \varphi ,\ \sin \varphi )+r{\dot {\varphi }}(-\sin \varphi ,\cos \varphi )$$

Аналогично, вторая производная положения частицы r равна ее ускорению a. $$\mathbf {a} ={\ddot {r}}(\cos \varphi ,\ \sin \varphi )+2{\dot {r}}{\dot {\varphi }}(-\sin \varphi ,\ \cos \varphi )+r{\ddot {\varphi }}(-\sin \varphi ,\cos \varphi )-r{\dot {\varphi }}^{2}(\cos \varphi ,\sin \varphi )$$

Скорость v и ускорение a можно выразить через радиальные и азимутальные единичные векторы. Радиальный единичный вектор получается путем деления вектора положения r на его величину r , как описано выше. $$\mathbf {\hat {r}} =(\cos \varphi ,\ \sin \varphi )$$

Азимутальный единичный вектор определяется выражением $${\hat {\boldsymbol {\varphi }}}=(-\sin \varphi ,\ \cos \varphi )$$

Таким образом, скорость можно записать как $$\mathbf {v} =v_{r}\mathbf {\hat {r}} +v_{\varphi }{\hat {\boldsymbol {\varphi }}}={\dot {r}}\mathbf {\hat {r}} +r{\dot {\varphi }}{\hat {\boldsymbol {\varphi }}}$$тогда как ускорение равно $$\mathbf {a} =a_{r}\mathbf {\hat {r}} +a_{\varphi }{\hat {\boldsymbol {\varphi }}}=({\ddot {r}}-r{\dot {\varphi }}^{2})\mathbf {\hat {r}} +(2{\dot {r}}{\dot {\varphi }}+r{\ddot {\varphi }}){\hat {\boldsymbol {\varphi }}}$$

Удельный угловой момент

Удельный угловой момент h равен скорости v , умноженной на r _⊥ , составляющей вектора положения r, перпендикулярной вектору скорости v . h также равно радиальному расстоянию r, умноженному на азимутальную составляющую v _φ скорости. Обе эти формулы равны rv cos β.

Смотрите также: Удельный угловой момент

Поскольку F = m a по второму закону движения Ньютона и поскольку F является центральной силой, то только радиальная составляющая ускорения a может быть отличной от нуля; угловая составляющая a _φ должна быть равна нулю $$a_{\varphi }=2{\dot {r}}{\dot {\varphi }}+r{\ddot {\varphi }}=0$$

Поэтому, $${\frac {d}{dt}}\left(r^{2}{\dot {\varphi }}\right)=r(2{\dot {r}}{\dot {\varphi }}+r{\ddot {\varphi }})=ra_{\varphi }=0$$

Это выражение в скобках обычно обозначается h $$h=r^{2}{\dot {\varphi }}=rv_{\varphi }=\left|\mathbf {r} \times \mathbf {v} \right|=vr_{\perp }={\frac {L}{m}}$$

что равно скорости v, умноженной на r _⊥ , компоненту радиус-вектора, перпендикулярной скорости. h - величина удельного углового момента , поскольку она равна величине L углового момента, деленной на массу m частицы.

Для краткости угловую скорость иногда записывают ω $$\omega ={\dot {\varphi }}={\frac {d\varphi }{dt}}$$

Однако не следует предполагать, что ω постоянна. Поскольку h постоянна, ω меняется с радиусом r по формуле $$\omega ={\frac {h}{r^{2}}}$$

Поскольку h постоянна и r ² положителен, угол φ монотонно изменяется в любой задаче о центральной силе, либо непрерывно увеличиваясь ( h положительный), либо непрерывно уменьшаясь ( h отрицательный).

Постоянная скорость по площадям

Поскольку площадь А равна 1 ⁄ 2   r _⊥ vt , земная скорость dA / dt (скорость, с которой A выметается частицей) равна 1 ⁄ 2  r _⊥ v  =  1 ⁄ 2 h .

См. также: Скорость по площади.

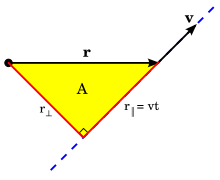
Величина h также равна удвоенной поверхностной скорости , которая представляет собой скорость, с которой частица выметает область относительно центра. Таким образом, пространственная скорость постоянна для частицы, на которую действует центральная сила любого типа; это второй закон Кеплера . И наоборот, если движение под действием консервативной силы F плоское и имеет постоянную продольную скорость для всех начальных условий радиуса r и скорости v , то азимутальное ускорение a _φ всегда равно нулю. Следовательно, согласно второму закону Ньютона F = m a , сила является центральной силой.

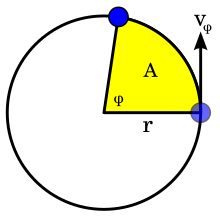
Постоянство поверхностной скорости можно проиллюстрировать равномерным круговым и линейным движением. При равномерном круговом движении частица движется с постоянной скоростью v по окружности радиуса r . Поскольку угловая скорость ω = v / r постоянна, площадь, выметаемая за время Δt , равна ω r ² Δ т ; следовательно, равные площади выметаются за одинаковое время Δt . При равномерном линейном движении (т. е. движении в отсутствие силы по первому закону движения Ньютона) частица движется с постоянной скоростью, т. е. с постоянной скоростью v вдоль прямой. За время Δt частица выметает область 1 ⁄ 2 v Δ tr _⊥ ( прицельный параметр ). Расстояние r⊥ _; не меняется при движении частицы вдоль линии он представляет собой расстояние наибольшего приближения линии к центру O ( прицельный параметр ). Поскольку скорость v также не меняется, то и окружная скорость 1 ⁄ 2 vr _⊥ — постоянная движения; частица сметает равные площади за одинаковое время.

Площадь A кругового сектора равна 1 ⁄ 2  r ² φ = 1 ⁄ 2  r ² ω т = 1 ⁄ 2   р   v _φ т . Следовательно, земная скорость dA/dt равна 1 ⁄ 2  r  v _φ  =  1 ⁄ ​   часа . Для равномерного кругового движения r и v _φ постоянны; таким образом, dA/dt также является постоянным.

Эквивалентное параллельное силовое поле

Преобразованием переменных любую задачу центральной силы можно преобразовать в эквивалентную задачу параллельной силы. Вместо обычных декартовых координат x и y две новые переменные положения ξ = x / y и η = 1/ y определяются , а также новая временная координата τ. $$\tau =\int {\frac {dt}{y^{2}}}$$

Соответствующие уравнения движения для ξ и η имеют вид $${\frac {d\xi }{d\tau }}={\frac {d}{dt}}\left({\frac {x}{y}}\right){\frac {dt}{d\tau }}=\left({\frac {{\dot {x}}y-{\dot {y}}x}{y^{2}}}\right)y^{2}=-h$$$${\frac {d\eta }{d\tau }}={\frac {d}{dt}}\left({\frac {1}{y}}\right){\frac {dt}{d\tau }}=-{\frac {\dot {y}}{y^{2}}}y^{2}=-{\dot {y}}$$

Поскольку скорость изменения ξ постоянна, ее вторая производная равна нулю. $${\frac {d^{2}\xi }{d\tau ^{2}}}=0$$

Поскольку это ускорение в направлении ξ и поскольку F = ma по второму закону Ньютона, отсюда следует, что сила в направлении ξ равна нулю. Следовательно, сила действует только в направлении η , что является критерием задачи о параллельных силах. В явном виде ускорение в направлении η равно $${\frac {d^{2}\eta }{d\tau ^{2}}}={\frac {dt}{d\tau }}{\frac {d}{dt}}\left({\frac {d\eta }{d\tau }}\right)=-y^{2}{\ddot {y}}=-{\frac {y^{3}}{mr}}F(r)$$потому что ускорение в направлении y равно $${\ddot {y}}={\frac {1}{m}}F_{y}={\frac {1}{m}}F(r)\,{\frac {y}{r}}$$

Здесь F _y обозначает y -компоненту центральной силы, а y / r равен косинусу угла между осью y и радиальным вектором r .

Общее решение

Уравнение Бине

См. Также: уравнение Бине.

Поскольку центральная сила F действует только по радиусу, то только радиальная составляющая ускорения отлична от нуля. Согласно второму закону движения Ньютона, величина F равна массе m , умноженной на величину ее радиального ускорения. частицы $$F(r)=m{\ddot {r}}-mr\omega ^{2}=m{\frac {d^{2}r}{dt^{2}}}-{\frac {mh^{2}}{r^{3}}}$$

Это уравнение имеет коэффициент интегрирования ${\frac {dr}{dt}}$$${\begin{aligned}F(r)\,dr&=F(r){\frac {dr}{dt}}\,dt\\&=m\left({\frac {dr}{dt}}{\frac {d^{2}r}{dt^{2}}}-{\frac {h^{2}}{r^{3}}}{\frac {dr}{dt}}\right)\,dt\\&={\frac {m}{2}}\,d\left[\left({\frac {dr}{dt}}\right)^{2}+\left({\frac {h}{r}}\right)^{2}\right]\end{aligned}}$$

Интеграция доходности $$\int ^{r}F(r)\,dr={\frac {m}{2}}\left[\left({\frac {dr}{dt}}\right)^{2}+\left({\frac {h}{r}}\right)^{2}\right]$$

Если h не равен нулю, независимую переменную можно изменить с t на φ. $${\frac {d}{dt}}=\omega {\frac {d}{d\varphi }}={\frac {h}{r^{2}}}{\frac {d}{d\varphi }}$$дающее новое уравнение движения $$\int ^{r}F(r)\,dr={\frac {mh^{2}}{2}}\left[\left(-{\frac {1}{r^{2}}}{\frac {dr}{d\varphi }}\right)^{2}+\left({\frac {1}{r}}\right)^{2}\right]$$

Делаем замену переменных на обратный радиус u = 1/ r урожайность

$$\left({\frac {du}{d\varphi }}\right)^{2}=C-u^{2}-G\left(u\right)$$ ( 1 )

где C — константа интегрирования, а функция G ( u ) определяется формулой $$G(u)=-{\frac {2}{mh^{2}}}\int ^{\frac {1}{u}}F(r)\,dr$$

Это уравнение становится квазилинейным при дифференцировании по φ $${\frac {d^{2}u}{d\varphi ^{2}}}+u=-{\frac {1}{mh^{2}u^{2}}}F(1/u)$$

Это известно как уравнение Бине . Интегрирование ( 1 ) дает решение для φ $$\varphi =\varphi _{0}+\int ^{\frac {1}{r}}{\frac {du}{\sqrt {C-u^{2}-G(u)}}}$$где φ0 _. — еще одна константа интегрирования Задача центральной силы называется «интегрируемой», если это окончательное интегрирование может быть решено в терминах известных функций.

Орбита частицы

Возьмите скалярное произведение второго закона движения Ньютона на скорость частицы, где сила получается из потенциальной энергии. $$m{\ddot {\mathbf {r} }}=\mathbf {F} =-{\boldsymbol {\nabla }}U(\mathbf {r} )\qquad \left/\;\cdot {\dot {\mathbf {r} }}\right.$$дает $$m{\dot {\mathbf {r} }}\cdot {\ddot {\mathbf {r} }}={\frac {1}{2}}m{\frac {d}{dt}}\left({\dot {\mathbf {r} }}\cdot {\dot {\mathbf {r} }}\right)=-{\dot {\mathbf {r} }}\cdot {\boldsymbol {\nabla }}U(\mathbf {r} )=-\sum _{i=1}^{3}{\frac {dx_{i}}{dt}}{\frac {\partial U}{\partial x_{i}}}={\frac {dU}{dt}}$$ где предполагается суммирование по пространственному декартову индексу $i=1,2,3$ и мы использовали тот факт, что ${\frac {d}{dt}}\left({\dot {\mathbf {r} }}\cdot {\dot {\mathbf {r} }}\right)={\ddot {\mathbf {r} }}\cdot {\dot {\mathbf {r} }}+{\dot {\mathbf {r} }}\cdot {\ddot {\mathbf {r} }}=2{\dot {\mathbf {r} }}\cdot {\ddot {\mathbf {r} }}$ и использовал цепное правило ${\frac {d}{dt}}U(x,y,z)=\sum _{i}{\frac {\partial U}{\partial x_{i}}}{\frac {dx_{i}}{dt}}$.Перестановка $${\frac {d}{dt}}\left({\frac {1}{2}}m{\dot {\mathbf {r} }}^{2}+U(\mathbf {r} )\right)=0$$Термин в круглых скобках слева является константой, обозначьте его как $E_{\mathrm {tot} }$, полная механическая энергия. Очевидно, что это сумма кинетической энергии и потенциальной энергии.

Более того, если потенциал является центральным, $U(x,y,z)=U(r)$ и поэтому сила действует в радиальном направлении. В этом случае векторное произведение второго закона движения Ньютона на вектор положения частицы $\mathbf {r}$ должно исчезнуть, поскольку векторное произведение двух параллельных векторов равно нулю: $$\mathbf {r} \times m{\ddot {\mathbf {r} }}={\frac {d}{dt}}\left(\mathbf {r} \times m{\dot {\mathbf {r} }}\right)-\left({\dot {\mathbf {r} }}\times m{\dot {\mathbf {r} }}\right)=\mathbf {r} \times \mathbf {F} =0$$ но ${\dot {\mathbf {r} }}\times m{\dot {\mathbf {r} }}=0$ (перекрестное произведение параллельных векторов), поэтому $${\frac {d}{dt}}\left(\mathbf {r} \times m{\dot {\mathbf {r} }}\right)=0$$ Термин в круглых скобках слева является константой, обозначьте его как $\mathbf {L}$ угловой момент, В частности, в полярных координатах $L=mrv_{\varphi }=r^{2}{\dot {\varphi }}$ или $${\dot {\varphi }}={\frac {L}{mr^{2}}}$$ Дальше, ${\dot {\mathbf {r} }}^{2}=v_{r}^{2}+v_{\varphi }^{2}={\dot {r}}^{2}+(r{\dot {\varphi }})^{2}$, поэтому уравнение энергии можно упростить, используя угловой момент как $$E_{\mathrm {tot} }={\frac {1}{2}}m{\dot {r}}^{2}+{\frac {1}{2}}mr^{2}{\dot {\varphi }}^{2}+U(r)={\frac {1}{2}}m{\dot {r}}^{2}+{\frac {L^{2}}{2mr^{2}}}+U(r)={\frac {1}{2}}m{\dot {r}}^{2}+U_{\mathrm {eff} }(r)$$Это указывает на то, что угловой момент вносит вклад в эффективную потенциальную энергию. $$U_{\mathrm {eff} }(r)=U(r)+{\frac {L^{2}}{2mr^{2}}}$$Решите это уравнение для ${\dot {r}}$$${\dot {r}}={\frac {dr}{dt}}={\sqrt {\frac {2}{m}}}{\sqrt {E_{\mathrm {tot} }-U_{\mathrm {eff} }(r)}}$$которую можно преобразовать к производной $r$ по азимутальному углу $\varphi$ как $${\frac {dr}{d\varphi }}={\frac {dr/dt}{d\varphi /dt}}={\frac {\dot {r}}{\dot {\varphi }}}={\frac {mr^{2}}{L}}{\sqrt {\frac {2}{m}}}{\sqrt {E_{\mathrm {tot} }-U_{\mathrm {eff} }(r)}}$$Это сепарабельное дифференциальное уравнение первого порядка. Интегрируем и получаем формулу $$\varphi =\varphi _{0}+{\frac {L}{\sqrt {2m}}}\int ^{r}{\frac {dr}{r^{2}{\sqrt {E_{\mathrm {tot} }-U_{\mathrm {eff} }(r)}}}}$$

Замена переменной интегрирования на обратный радиус дает интеграл $$\varphi =\varphi _{0}+\int ^{u}{\frac {du}{\sqrt {{\frac {2m}{L^{2}}}E_{\mathrm {tot} }-{\frac {2m}{L^{2}}}U(1/u)-u^{2}}}}$$что выражает указанные выше константы C = 2 mE _tot / L ² и G ( ты ) = 2 мU (1/ ты )/ L ² выше в терминах полной энергии E _tot и потенциальной энергии U ( r ).

Точки поворота и замкнутые орбиты

Основная статья: теорема Бертрана

Скорость изменения r равна нулю, если эффективная потенциальная энергия равна полной энергии. $$E_{\mathrm {tot} }=U(r)+{\frac {L^{2}}{2mr^{2}}}$$

Точки, в которых это уравнение удовлетворяется, известны как точки поворота . Орбита по обе стороны от точки поворота симметрична; другими словами, если азимутальный угол определен так, что φ = 0 в точке поворота, то орбита одинакова в противоположных направлениях, r ( φ ) = r (− φ ).

Если есть две точки поворота, такие что радиус r ограничен между r _min и r _max , то движение содержится в кольце этих радиусов. При изменении радиуса от одной точки поворота к другой изменение азимутального угла φ равно $$\Delta \varphi ={\frac {L}{\sqrt {2m}}}\int _{r_{\min }}^{r_{\max }}{\frac {dr}{r^{2}{\sqrt {E-U(r)-{\frac {L^{2}}{2mr^{2}}}}}}}$$

Орбита замкнется сама собой при условии, что Δφ равно рациональной дроби 2 π , т. е. $$\Delta \varphi =2\pi {\frac {m}{n}}$$где m и n — целые числа. В этом случае радиус колеблется ровно m раз, а азимутальный угол φ совершает ровно n оборотов. Однако в общем случае Δφ/2π не будет таким рациональным числом , и, следовательно, орбита не будет замкнутой. В этом случае частица в конечном итоге пройдет сколь угодно близко к каждой точке внутри кольца. Два типа центральной силы всегда создают замкнутые орбиты: F ( r ) = α r (линейная сила) и F ( r ) = α/ r. ² ( закон обратных квадратов ). Как показал Бертран, эти две центральные силы — единственные, которые гарантируют замкнутость орбит.

В общем случае, если угловой момент L не равен нулю, L ² /2 мр ² Член предотвращает попадание частицы в начало координат, если только эффективная потенциальная энергия не стремится к отрицательной бесконечности в пределе, когда r стремится к нулю. Следовательно, если есть единственная точка поворота, орбита обычно уходит в бесконечность; точка поворота соответствует точке минимального радиуса.

Конкретные решения

проблема Кеплера

Классическая гравитация — это центральная сила. Решение этой проблемы центральной силы показывает, что связанная частица движется по эллиптической орбите, на которой равные площади выметаются за одинаковое время, как описано вторым законом Кеплера .

См. Также: проблема Кеплера и вектор Лапласа – Рунге – Ленца.

В классической физике многие важные силы подчиняются закону обратных квадратов, например гравитация или электростатика . Общая математическая форма таких центральных сил, обратных квадратам, такова: $$F={\frac {\alpha }{r^{2}}}=\alpha u^{2}$$для постоянного $\alpha$, что отрицательно для силы притяжения и положительно для силы отталкивания.

Этот частный случай классической проблемы центральной силы называется проблемой Кеплера . Для силы, обратного квадрату, полученное выше уравнение Бине является линейным. $${\frac {d^{2}u}{d\varphi ^{2}}}+u=-{\frac {\alpha }{mh^{2}}}.$$

Решение этого уравнения есть $$u(\varphi )=-{\frac {\alpha }{mh^{2}}}\left[1+e\cos \left(\varphi -\varphi _{0}\right)\right]$$из которого видно, что орбита представляет собой коническое сечение с эксцентриситетом е ; здесь φ ₀ — начальный угол, а центр силы находится в фокусе конического сечения. Используя формулу половинного угла для синуса , это решение также можно записать как $$u(\varphi )=u_{1}+(u_{2}-u_{1})\sin ^{2}\left({\frac {\varphi -\varphi _{0}}{2}}\right)$$

Что касается всех центральных сил, частица в задаче Кеплера заметает равные площади за одинаковое время, как показано двумя синими эллиптическими секторами. Центр силы расположен в одном из фокусов эллиптической орбиты.

где u ₁ и u ₂ — константы, причем u ₂ больше, чем u ₁ . Два варианта решения связаны уравнениями $$u_{1}+u_{2}={\frac {-2\alpha }{mh^{2}}}$$и $$e={\frac {u_{2}-u_{1}}{u_{2}+u_{1}}}$$

Поскольку грех ² функция всегда больше нуля, u ₂ — максимально возможное значение u и обратное наименьшему возможному значению r , т. е. расстояние наибольшего сближения ( периапсис ). Поскольку радиальное расстояние r не может быть отрицательным числом, то и обратное ему число u не может быть отрицательным ; следовательно, u ₂ должно быть положительным числом. Если u ₁ также положительное значение, это наименьшее возможное значение u , которое соответствует максимально возможному значению r , расстоянию самого дальнего приближения ( апоапсис ). Если u ₁ равно нулю или отрицательно, то наименьшее возможное значение u равно нулю (орбита уходит в бесконечность); в этом случае единственными релевантными значениями φ являются те, которые делают u положительным.

Для силы притяжения (α < 0) орбита представляет собой эллипс , гиперболу или параболу , в зависимости от того, является ли u ₁ положительным, отрицательным или нулевым соответственно; это соответствует эксцентриситету e меньше единицы, больше единицы или равному единице. Для отталкивающей силы (α > 0) u ₁ должна быть отрицательной, так как u ₂ положительна по определению и их сумма отрицательна; следовательно, орбита является гиперболой. Естественно, если силы нет (α=0), орбита представляет собой прямую линию.

Центральные силы с точными решениями

Смотрите также: Точные решения классических задач центральной силы.

Уравнение Бине для u ( φ ) можно решить численно практически для любой центральной силы F (1/ u ). Однако лишь немногие силы приводят к формулам для u в терминах известных функций. Как было получено выше, решение для φ можно выразить в виде интеграла по u $$\varphi =\varphi _{0}+{\frac {L}{\sqrt {2m}}}\int ^{u}{\frac {du}{\sqrt {E_{\mathrm {tot} }-U(1/u)-{\frac {L^{2}u^{2}}{2m}}}}}$$

Задача центральной силы называется «интегрируемой», если это интегрирование может быть решено в терминах известных функций.

Если сила является степенным законом, т. е. если F ( r ) = α r ^н , то u можно выразить через круговые функции и/или эллиптические функции , если n равно 1, -2, -3 (круговые функции) и -7, -5, -4, 0, 3, 5, -3/2. , -5/2, -1/3, -5/3 и -7/3 (эллиптические функции). Аналогично, только шесть возможных линейных комбинаций степенных законов дают решения в терминах круговых и эллиптических функций. $$F(r)=Ar^{-3}+Br+Cr^{3}+Dr^{5}$$$$F(r)=Ar^{-3}+Br+Cr^{-5}+Dr^{-7}$$$$F(r)=Ar^{-3}+Br^{-2}+Cr+D$$$$F(r)=Ar^{-3}+Br^{-2}+Cr^{-4}+Dr^{-5}$$$$F(r)=Ar^{-3}+Br^{-2}+Cr^{-3/2}+Dr^{-5/2}$$$$F(r)=Ar^{-3}+Br^{-1/3}+Cr^{-5/3}+Dr^{-7/3}$$

Следующие частные случаи первых двух типов сил всегда приводят к круговым функциям. $$F(r)=Ar^{-3}+Br$$$$F(r)=Ar^{-3}+Br^{-2}$$

Особый случай $$F(r)=Ar^{-5}$$ был упомянут Ньютоном в следствии 1 к предложению VII «Начал» как сила, подразумеваемая круговыми орбитами, проходящими через точку притяжения.

Вращающиеся орбиты

Duration: 17 seconds.0:17

Иллюстрация теоремы Ньютона о вращающихся орбитах. Зеленая планета совершает одну (субгармоническую) орбиту на каждые три оборота голубой планеты ( k =1/3). GIF - версию этой анимации можно найти здесь .

Основная статья: Теорема Ньютона о вращающихся орбитах

Термин р ⁻³ встречается во всех приведенных выше законах силы, что указывает на то, что добавление силы обратного куба не влияет на разрешимость задачи в терминах известных функций. Ньютон показал, что при корректировке начальных условий добавление такой силы не влияет на радиальное движение частицы, а умножает ее угловое движение в постоянный коэффициент k . Расширение теоремы Ньютона было обнаружено в 2000 году Магомедом и Вавдой.

Предположим, что частица движется под действием произвольной центральной силы F ₁ ( r ), и пусть ее радиус r и азимутальный угол φ обозначаются как r ( t ) и φ ₁ ( t ) как функция времени t . Теперь рассмотрим вторую частицу с той же массой m , которая имеет такое же радиальное движение r ( t ), но угловая скорость которой в k раз выше, чем у первой частицы. Другими словами, азимутальные углы двух частиц связаны уравнением φ ₂ ( t ) = k   φ ₁ ( t ). Ньютон показал, что сила, действующая на вторую частицу, равна силе F ₁ ( r ), действующей на первую частицу, плюс центральная сила обратного куба. $$F_{2}(r)=F_{1}(r)+{\frac {L_{1}^{2}}{mr^{3}}}\left(1-k^{2}\right)$$где L ₁ — величина углового момента первой частицы .

Если к ² больше единицы, F ₂ − F ₁ — отрицательное число; таким образом, добавленная сила обратного куба является притягивающей . И наоборот, если k ² меньше единицы, F ₂ − F ₁ – положительное число; добавленная сила обратного куба является отталкивающей . Если k — целое число, например 3, говорят, что орбита второй частицы является гармоникой орбиты первой частицы; напротив, если k является обратным целому числу, например 1 ⁄ 3 вторая орбита называется субгармоникой первой орбиты.

Историческое развитие

Рисунок 10: Геометрическое доказательство Ньютона о том, что движущаяся частица сметает равные площади за равное время тогда и только тогда, когда сила, действующая на нее в точке B, является центральной силой. Здесь треугольник OAB имеет ту же площадь, что и треугольники OBC и OBK.

Вывод Ньютона

Классическая проблема центральной силы была геометрически решена Исааком Ньютоном в его «Philosophiæ Naturalis Principia Mathematica» , в которой Ньютон представил свои законы движения . Ньютон использовал эквивалент чехарды для преобразования непрерывного движения в дискретное, чтобы можно было применить геометрические методы. В этом подходе положение частицы рассматривается только в равномерно расположенные моменты времени. Для иллюстрации: частица на рисунке 10 расположена в точке A в момент времени t = 0, в точке в момент времени t = ∆t , в точке C в момент времени t = 2∆t ∆t и так далее для всех моментов времени t = n B . , где n — целое число. Предполагается, что скорость между этими моментами времени постоянна. Таким образом, вектор r _AB = r _B - r _A равен Δ t, умноженному на вектор скорости v _AB (красная линия), тогда как r _BC = r _C - r _B равен v _BC Δ t (синяя линия). Поскольку скорость между точками постоянна, предполагается, что сила действует мгновенно в каждой новой позиции; например, сила, действующая на частицу в точке B, мгновенно меняет скорость от от _AB до v _BC . Вектор разности Δ r = r _BC - r _AB равен Δ v Δ t (зеленая линия), где Δ v = v _BC - v _AB — это изменение скорости в результате действия силы в B. точке Поскольку ускорение a параллельно Δ v и поскольку F = m a , сила F должна быть параллельна Δ v и Δ r . Если F — центральная сила, она должна быть параллельна вектору r _B от центра O до точки B (пунктирная зеленая линия); случае Δr также параллелен rB _. в этом

Если в точке B не действует никакая сила , скорость не изменится, и частица достигнет точки K за время t = 2Δt . Площади треугольников OAB и OBK равны, потому что они имеют одно и то же основание ( r _AB ) и высоту ( r _⊥ ). Если Δr параллелен rB , _, треугольники OBK и OBC также равны, поскольку они имеют одно и то же основание ( ) _rB а высота не меняется. В этом случае площади треугольников OAB и OBC одинаковы, и частица за одинаковое время выметает равные площади. Обратно, если площади всех таких треугольников равны, то ∆r должна быть параллельна r _B , откуда следует, что F — центральная сила. Таким образом, частица сметает равные площади за одинаковое время тогда и только тогда, когда F — центральная сила.

Альтернативные выводы уравнений движения

Лагранжева механика

Формулу радиальной силы можно также получить с помощью лагранжевой механики . В полярных координатах лагранжиан L одиночной частицы в поле потенциальной энергии U ( r ) определяется выражением $$L={\frac {1}{2}}m{\dot {r}}^{2}+{\frac {1}{2}}mr^{2}{\dot {\varphi }}^{2}-U(r)$$

Тогда уравнения движения Лагранжа $${\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {r}}}}\right)={\frac {\partial L}{\partial r}}$$принять форму $$m{\ddot {r}}=mr{\dot {\varphi }}^{2}-{\frac {dU}{dr}}={\frac {mh^{2}}{r^{3}}}+F(r)$$поскольку величина F ( r ) радиальной силы равна отрицательной производной потенциальной энергии U ( r ) в радиальном направлении.

гамильтонова механика

Формула радиальной силы также может быть получена с использованием гамильтоновой механики . В полярных координатах гамильтониан можно записать как $$H={\frac {1}{2m}}\left(p_{r}^{2}+{\frac {p_{\varphi }^{2}}{r^{2}}}\right)+U(r)$$

Поскольку азимутальный угол φ не входит в гамильтониан, его сопряженный импульс p _φ является константой движения. Этот сопряженный импульс представляет собой величину L углового момента, как показано гамильтоновым уравнением движения для φ $${\frac {d\varphi }{dt}}={\frac {\partial H}{\partial p_{\varphi }}}={\frac {p_{\varphi }}{mr^{2}}}={\frac {L}{mr^{2}}}$$

Соответствующее уравнение движения для r имеет вид $${\frac {dr}{dt}}={\frac {\partial H}{\partial p_{r}}}={\frac {p_{r}}{m}}$$

Взяв вторую производную r по времени и используя уравнение движения Гамильтона для p _r, получаем уравнение радиальной силы $${\frac {d^{2}r}{dt^{2}}}={\frac {1}{m}}{\frac {dp_{r}}{dt}}=-{\frac {1}{m}}\left({\frac {\partial H}{\partial r}}\right)={\frac {p_{\varphi }^{2}}{m^{2}r^{3}}}-{\frac {1}{m}}{\frac {dU}{dr}}={\frac {L^{2}}{m^{2}r^{3}}}+{\frac {1}{m}}F(r)$$

Уравнение Гамильтона-Якоби

Орбитальное уравнение может быть получено непосредственно из уравнения Гамильтона – Якоби . Приняв радиальное расстояние r и азимутальный угол φ в качестве координат, уравнение Гамильтона-Якоби для задачи центральной силы можно записать $${\frac {1}{2m}}\left({\frac {dS_{r}}{dr}}\right)^{2}+{\frac {1}{2mr^{2}}}\left({\frac {dS_{\varphi }}{d\varphi }}\right)^{2}+U(r)=E_{\mathrm {tot} }$$где S = S _φ ( φ ) + S _r ( r ) − E _tot t — главная функция Гамильтона , а E _tot и t представляют собой полную энергию и время соответственно. Это уравнение может быть решено путем последовательного интегрирования обыкновенных дифференциальных уравнений , начиная с φ уравнения . $${\frac {dS_{\varphi }}{d\varphi }}=p_{\varphi }=L$$где pφ _равная — константа движения, момента импульса L. величине Таким образом, S _φ (φ) = L φ и уравнение Гамильтона–Якоби принимает вид $${\frac {1}{2m}}\left({\frac {dS_{r}}{dr}}\right)^{2}+{\frac {L^{2}}{2mr^{2}}}+U(r)=E_{\mathrm {tot} }$$

Интегрирование этого уравнения для S _r дает $$S_{r}(r)={\sqrt {2m}}\int dr{\sqrt {E_{\mathrm {tot} }-U(r)-{\frac {L^{2}}{2mr^{2}}}}}$$

Взяв производную от S по L, получим орбитальное уравнение, полученное выше. $$\varphi _{0}={\frac {\partial S}{\partial L}}={\frac {\partial S_{\varphi }}{\partial L}}+{\frac {\partial S_{r}}{\partial L}}=\varphi -{\frac {L}{\sqrt {2m}}}\int ^{r}{\frac {dr}{r^{2}{\sqrt {E_{\mathrm {tot} }-U(r)-{\frac {L^{2}}{2mr^{2}}}}}}}$$

См. также

• Геодезическая Шварцшильда , аналог общей теории относительности.
• Частица в сферически-симметричном потенциале , аналог в квантовой механике.
• Водородоподобный атом , проблема Кеплера в квантовой механике
• Обратноквадратичный потенциал

Библиография

• Гольдштейн, Х. (1980). Классическая механика (2-е изд.). Ридинг, Массачусетс: Аддисон-Уэсли. ISBN  0-201-02918-9 .
• Ландау Л.Д. и Лифшиц Э.М. (1976). Механика . Курс теоретической физики (3-е изд.). Нью-Йорк: Пергамон Пресс. ISBN  0-08-029141-4 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
• Миснер К.В. , Торн К. и Уиллер Дж.А. (1973). Гравитация . Сан-Франциско: WH Freeman. ISBN  978-0-7167-0344-0 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
• Зоммерфельд, А. (1970). Механика . Лекции по теоретической физике . Том. Я (4-е изд.). Нью-Йорк: Академическая пресса. ISBN  978-0-12-654670-5 .
• Саймон КР (1971). Механика (3-е изд.). Ридинг, Массачусетс: Аддисон-Уэсли. ISBN  0-201-07392-7 .
• Уиттакер, ET (1937). Трактат об аналитической динамике частиц и твердых тел с введением в проблему трех тел (4-е изд.). Нью-Йорк: Dover Publications. ISBN  978-0-521-35883-5 .

Внешние ссылки

• «Задачи двух тел о центральной силе» , Д.Э. Гэри из Технологического института Нью-Джерси.
• Движение в поле центральной силы. Архивировано 21 сентября 2018 г. в Wayback Machine А. Бризаром из колледжа Святого Михаила.
• Движение под влиянием центральной силы , Дж. У. Коллинз, II из Университета Кейс Вестерн Резерв.
• Видеолекция WHG Lewin из Массачусетского технологического института