Принцип самосогласования Новикова
Принцип самосогласованности Новикова , также известный как гипотеза самосогласованности Новикова и Ларри Нивена , закон сохранения истории — это принцип, разработанный российским физиком Игорем Дмитриевичем Новиковым в середине 1980-х годов. Новиков намеревался решить проблему парадоксов в путешествиях во времени , что теоретически допускается в некоторых решениях общей теории относительности , содержащих так называемые замкнутые времениподобные кривые . Этот принцип утверждает, что если существует событие, которое могло бы вызвать парадокс или какое-либо «изменение» в прошлом, то вероятность этого события равна нулю. Таким образом, было бы невозможно создавать временные парадоксы .
История
[ редактировать ]Физикам давно известно, что некоторые решения общей теории относительности содержат замкнутые времениподобные кривые — например, метрика Гёделя . Новиков обсуждал возможность создания замкнутых времяподобных кривых (КТК) в книгах, написанных им в 1975 и 1983 годах. [1] высказывая мнение, что разрешены только самосогласованные путешествия во времени. [2] В статье Новикова и некоторых других 1990 года « Задача Коши в пространстве-времени с замкнутыми времяподобными кривыми» [3] авторы заявляют:
Единственный тип нарушения причинности, который авторы сочли неприемлемым, — это тот, который воплощен в научно-фантастической концепции возвращения во времени и убийства себя в более молодом возрасте («изменение прошлого»). Несколько лет назад один из нас (Новиков) вкратце рассмотрел возможность существования CTC и заявил, что они не могут повлечь за собой такого рода нарушение причинности: события в CTC уже гарантированно самосогласованы, утверждал Новиков; они влияют друг на друга по замкнутой кривой саморегулирующимся, циклическим и самосогласованным образом. Другие авторы недавно пришли к той же точке зрения.
Мы воплотим эту точку зрения в принципе самосогласованности, который утверждает, что единственными решениями законов физики, которые могут возникнуть локально в реальной Вселенной, являются те, которые являются глобально самосогласованными. Этот принцип позволяет построить локальное решение уравнений физики только в том случае, если это локальное решение можно расширить до части (не обязательно уникального) глобального решения, которое четко определено во всех несингулярных областях пространства-времени.
Среди соавторов этой статьи 1990 года были Кип Торн , Майк Моррис и Ульви Юрцевер, которые в 1988 году пробудили новый интерес к теме путешествий во времени в общей теории относительности своей статьей «Червоточины, машины времени и слабая энергия». Состояние", [4] который показал, что новое решение общей теории относительности, известное как проходимая червоточина , может привести к замкнутым времениподобным кривым, и в отличие от предыдущих решений, содержащих CTC, оно не требует нереалистичных условий для Вселенной в целом. После обсуждений с ведущим автором статьи 1990 года Джоном Фридманом они убедили себя в том, что путешествие во времени не обязательно должно приводить к неразрешимым парадоксам, независимо от того, какой объект был отправлен через червоточину. [5] : 509

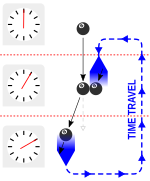
В ответ физик Джозеф Полчински написал им письмо, в котором утверждал, что можно избежать проблемы свободы воли, применив потенциально парадоксальный мысленный эксперимент с бильярдным шаром , отправленным назад во времени через червоточину. В сценарии Полчинского бильярдный шар запускается в червоточину под таким углом, что, если он продолжит движение по своему пути, он выйдет в прошлом под правильным углом и столкнется с самим собой, сбивая его с пути и предотвращая его. в первую очередь от входа в червоточину. В 1994 году Торн назвал этот сценарий « парадоксом Полчинского ». [6] : 510–511
Рассмотрев сценарий, Фернандо Эчеверриа и Гуннар Клинкхаммер, два студента Калифорнийского технологического института (где преподавал Торн), пришли к решению проблемы, которое включает в себя те же элементы, что и решение Фейнмана и Уиллера. [7] решение, называемое «скользящим ударом», чтобы избежать несоответствий, возникающих из-за петель причинно-следственной связи. В пересмотренном сценарии шар из будущего появляется под другим углом, отличным от того, который порождает парадокс, и наносит скользящий удар своему более молодому «я», вместо того, чтобы полностью выбить его из червоточины. Этот удар меняет его траекторию ровно на нужную степень, а это означает, что он переместится назад во времени под углом, необходимым для того, чтобы нанести самому молодому «я» необходимый скользящий удар. Эчеверрия и Клинкхаммер фактически обнаружили, что существует более одного самосогласованного решения со слегка разными углами для скользящего удара в каждой ситуации. Более поздний анализ Торна и Роберта Форварда показал, что для некоторых начальных траекторий бильярдного шара на самом деле может существовать бесконечное количество самосогласованных решений. [6] : 511–513
Эчеверриа, Клинкхаммер и Торн опубликовали статью, в которой обсуждались эти результаты, в 1991 году; [8] кроме того, они сообщили, что пытались выяснить, можно ли найти какие-либо начальные условия для бильярдного шара, для которых не существовало самосогласованных расширений, но не смогли этого сделать. Таким образом, вполне вероятно, что существуют самосогласованные расширения для каждой возможной начальной траектории, хотя это не доказано. [9] : 184 Это применимо только к начальным условиям за пределами области пространства-времени, нарушающей хронологию. [9] : 187 который ограничен горизонтом Коши . [10] Это может означать, что принцип самосогласованности Новикова на самом деле не накладывает никаких ограничений на системы за пределами области пространства-времени, где возможны путешествия во времени, а только внутри нее.
Даже если самосогласованные расширения могут быть найдены для произвольных начальных условий за пределами горизонта Коши, обнаружение того, что может быть несколько различных самосогласованных расширений для одного и того же начального условия - действительно, Echeverria et al. нашли бесконечное количество непротиворечивых расширений для каждой проанализированной ими начальной траектории [9] : 184 — можно рассматривать как проблематичный, поскольку в классическом понимании не существует способа решить, какое расширение выберут законы физики. Чтобы обойти эту трудность, Торн и Клинкхаммер проанализировали сценарий с бильярдным шаром, используя квантовую механику. [6] : 514–515 выполнив квантово-механическое суммирование по историям ( интеграл по путям ), используя только непротиворечивые расширения, и обнаружил, что это приводит к четко определенной вероятности для каждого непротиворечивого расширения. Авторы «Задачи Коши в пространстве-времени с замкнутыми времяподобными кривыми» пишут:
Самый простой способ навязать принцип самосогласованности в квантовой механике (в классическом пространстве-времени) — это формулировка суммы по историям, в которую включаются все те и только те истории, которые самосогласованы. Оказывается, что, по крайней мере формально (по модулю таких вопросов, как сходимость суммы), для каждого выбора начальной нерелятивистской волновой функции бильярдного шара перед горизонтом Коши такая сумма по историям дает уникальные, самосогласованные вероятности для результаты всех наборов последующих измерений. ... В более общем плане мы подозреваем, что для любой квантовой системы в классическом пространстве-времени-червоточине со стабильным горизонтом Коши сумма по всем самосогласованным историям даст уникальные, самосогласованные вероятности результатов всех наборов измерений, которые можно было бы решить сделать.
Предположения
[ редактировать ]Принцип непротиворечивости Новикова предполагает определенные условия относительно того, какие путешествия во времени возможны. В частности, предполагается, что либо существует только одна временная шкала , либо что любые альтернативные временные шкалы (например, те, которые постулируются многомировой интерпретацией квантовой механики ) недоступны.
Учитывая эти предположения, ограничение, согласно которому путешествия во времени не должны приводить к противоречивым результатам, можно рассматривать просто как тавтологию , самоочевидную истину, которая не может быть ложной. Однако принцип самосогласованности Новикова призван выйти за рамки простого утверждения о том, что история должна быть последовательной, и сделать дополнительное нетривиальное предположение о том, что Вселенная подчиняется тем же локальным законам физики в ситуациях, связанных с путешествиями во времени, что и в регионах пространства. время, лишенное замкнутых времяподобных кривых. Это поясняется в упомянутой выше «задаче Коши в пространствах-временях с замкнутыми времениподобными кривыми». [3] где авторы пишут:
То, что принцип самосогласованности не является полностью тавтологичным, становится ясным, если рассмотреть следующую альтернативу: законы физики могут допускать существование ЦТК; и когда происходят CTC, они могут вызвать новые виды локальной физики, с которыми мы ранее не встречались. ... Принцип самосогласования призван исключить такое поведение. Он настаивает на том, что локальная физика управляется теми же физическими законами, с которыми мы имеем дело в отсутствие ЦТК: законами, которые влекут за собой самосогласованную однозначность полей. По сути, принцип самосогласованности — это принцип не новой физики. Если кто-то с самого начала склонен игнорировать или обесценивать возможность новой физики, то он будет считать самосогласованность тривиальным принципом.
Последствия для путешественников во времени
[ редактировать ]Предположения принципа самосогласованности можно распространить на гипотетические сценарии, в которых участвуют разумные путешественники во времени, а также неразумные объекты, такие как бильярдные шары. Авторы «Задачи Коши в пространстве-времени с замкнутыми времяподобными кривыми » прокомментировали этот вопрос в заключении статьи, написав:
Если CTC разрешены и если приведенное выше видение приспособления к ним теоретической физики окажется более или менее правильным, то что это будет означать для философского понятия свободы воли для людей и других разумных существ? Это, безусловно, будет означать, что разумные существа не могут изменить прошлое. Такое изменение несовместимо с принципом самосогласованности. Следовательно, любое существо, которое прошло через червоточину и попыталось изменить прошлое, было бы запрещено физическим законом произвести изменение; т. е. «свободная воля» существа будет ограничена. Хотя это ограничение имеет более глобальный характер, чем ограничения свободы воли, вытекающие из стандартных локальных законов физики, для нас не очевидно, что это ограничение более строгое, чем ограничения, налагаемые стандартным физическим законом. [3]
Точно так же физик и астроном Дж. Крейг Уиллер заключает, что:
Согласно гипотезе согласованности, любые сложные межличностные взаимодействия должны осуществляться самосогласованно, чтобы не было парадоксов. Таково решение. Если понимать буквально, это означает, что если машины времени существуют, то свободной воли быть не может. Вы не сможете заставить себя убить себя в молодости, если отправитесь в прошлое. Вы можете сосуществовать, пойти выпить пива, вместе отпраздновать день рождения, но почему-то обстоятельства будут диктовать, что вы не можете вести себя так, чтобы это привело к парадоксу во времени. Новиков подкрепляет эту точку зрения другим аргументом: физика и так каждый день ограничивает вашу свободу воли. Вы можете захотеть полететь или пройти сквозь бетонную стену, но гравитация и физика конденсированного состояния диктуют вам, что вы не можете этого сделать. Почему, спрашивает Новиков, на путешественника во времени налагается другое ограничение последовательности? [11]
Логика временного цикла
[ редактировать ]Логика временной петли, придуманная робототехником и футуристом Гансом Моравецом . [12] — это гипотетическая система вычислений, которая использует принцип самосогласованности Новикова для вычисления ответов намного быстрее, чем это возможно при использовании стандартной модели вычислительной сложности с использованием машин Тьюринга . В этой системе компьютер отправляет результат вычисления назад во времени и полагается на принцип самосогласованности, чтобы обеспечить правильность отправленного результата, при условии, что машина может надежно получать информацию из будущего и предоставляет алгоритм и основной механизм. верны формально . Неверный результат или отсутствие результата все равно может быть получено, если точность механизма или алгоритма путешествия во времени не гарантирована.
Простым примером является алгоритм итерационного метода . Моравец заявляет:
Создайте вычислительный блок, который принимает входные данные, представляющие собой приблизительное решение некоторой проблемы, и выдает выходные данные, представляющие собой улучшенное приближение. Традиционно вы применяете такое вычисление несколько раз конечное число раз, а затем соглашаетесь на лучший, но все же приблизительный результат. При соответствующей отрицательной задержке возможно и другое: [...] результат каждой итерации функции возвращается во времени, чтобы служить «первым» приближением. Как только машина активируется, сразу и устойчиво (по исключительному совпадению!) появляется так называемая «фиксированная точка» F, входной сигнал, который дает идентичный выходной сигнал, обычно сигнализирующий об идеальном ответе. [...] Если итерация не сходится, то есть если F не имеет фиксированной точки, выходы и входы компьютера отключатся или зависнут в маловероятном промежуточном состоянии.
Квантовые вычисления с отрицательной задержкой
[ редактировать ]Физик Дэвид Дойч показал в 1991 году, что эта модель вычислений может решать задачи NP за полиномиальное время . [13] и Скотт Ааронсон позже расширил этот результат, чтобы показать, что модель также можно использовать для решения задач PSPACE за полиномиальное время. [14] [15] Дойч показывает, что квантовые вычисления с отрицательной задержкой (путешествие во времени назад) дают только самосогласованные решения, а область, нарушающая хронологию, накладывает ограничения, которые не очевидны с помощью классических рассуждений. [13] В 2014 году исследователи опубликовали моделирование, в котором, как они утверждают, подтвердили модель Дойча с фотонами. [16] Однако в статье Толксдорфа и Верха было показано, что условие самосогласования Дойча может выполняться с любой точностью в любой квантовой системе, описываемой в соответствии с релятивистской квантовой теорией поля, даже в пространстве-времени, которое не допускает замкнутых времяподобных кривых, что ставит под сомнение возможность Модель Дойча действительно характерна для квантовых процессов, моделирующих замкнутые времяподобные кривые в смысле общей теории относительности . [17] В более поздней статье [18] те же авторы показывают, что условие фиксированной точки CTC Дойча также может выполняться в любой системе.подчиняется законам классической статистической механики , даже если она не построена квантовыми системами. Авторы приходят к выводу, что, следовательно, Условие Дойча не является специфичным для квантовой физики и не зависит от квантовой природы физической системы, поэтому оно может быть выполнено.В результате Толксдорф и Верч утверждают, что условие Дойча недостаточно конкретно, чтобы позволить утверждать о сценариях путешествий во времени или их гипотетической реализации с помощью квантовой физики.
Рецепт Ллойда
[ редактировать ]Альтернативное предложение позже было представлено Сетом Ллойдом. [19] [20] на основе пост-селекции и интегралов по траектории. В частности, интеграл по путям относится к однозначным полям, что приводит к самосогласованным историям.
В популярной культуре
[ редактировать ]- «Последний обратный отсчет» (1980): научно-фантастический фильм о путешествиях во времени, в котором авианосец « Нимиц» проходит через червоточину обратно в канун нападения японцев на Перл-Харбор . Аномалия возвращается и отправляет его обратно в настоящее, прежде чем у него появится шанс повлиять на результат.
- Рассказ «Купец и ворота алхимика » (2007) Теда Чанга исследует взаимодействие между свободой воли и самосогласованным путешествием во времени.
- Steins;Gate (2009): Цитируется Макисе Курису во время ее презентации о путешествиях во времени.
- Гарри Поттер и методы рационального мышления : В изложении рациональности Элиэзера Юдковского, оформленном как часть фанфика о Гарри Поттере, Гарри пытается использовать свой Маховик Времени, чтобы повлиять на прошлое, и приходит к выводу, что применим принцип самосогласованности Новикова.
- Ортогональный : серия научно-фантастических романов Грега Игана , в которой применяется этот принцип.
- Сериал Netflix «Тьма» во многом основан на идее о том, что возможность путешествия во времени соблазняет персонажей попытаться изменить прошлое, что приводит их только к возникновению событий, которые они пытались предотвратить в первую очередь.
- Quantum Break (2016): видеоигра от Remedy Entertainment , в центре внимания которой находится вопрос, можно ли изменить прошлое или нет. Некоторые персонажи сюжета вынуждены его изменить, тогда как другие, которые уже тщетно пытались это сделать, смирились и пришли к выводу, что принцип самосогласованности Новикова, по-видимому, применим.
- Outer Wilds (2019): видеоигра, включающая путешествие во времени, которая не следует этому принципу и приводит к завершению игры, если игрок экспериментирует с целью ее проверки.
- Все путешествия во времени в канала Hallmark Channel оригинальном сериале «Дорога домой» следуют принципу самосогласованности Новикова. Двое главных героев могут путешествовать во времени назад, прыгнув в пруд, но изменить что-либо в прошлом они не в состоянии. Все их действия становятся частью истории и фактически становятся причиной тех трагических событий, которые они пытались предотвратить.
См. также
[ редактировать ]- Причинно-следственная петля
- Причинность (физика)
- Гипотеза о защите хронологии
- Гипотеза космической цензуры
- Курица или яйцо
- Многомировая интерпретация
- Парадокс дедушки
- Квантовая механика путешествий во времени
- Просмотр времени
Ссылки
[ редактировать ]- ^ См. примечание 10 на стр. 42 Фридмана и др., «Задача Коши в пространстве-времени с замкнутыми времяподобными кривыми».
- ^ На стр. 169 книги Новикова «Эволюция Вселенной» (1983), которая представляла собой перевод его русской книги «Эволюция Вселенной» (1979), комментарий Новикова по этому вопросу передан переводчиком М. М. Баско так: «Замыкание временных кривых не обязательно означает нарушение причинность, поскольку все события на такой замкнутой линии могут быть «саморегулирующимися» — все они влияют друг на друга в рамках замкнутого цикла и следуют друг за другом самосогласованным образом».
- ^ Перейти обратно: а б с Фридман, Джон; Майкл Моррис; Игорь Новиков; Фернандо Эчеверрия; Гуннар Клинкхаммер; Кип Торн; Ульви Юрцевер (1990). «Задача Коши в пространстве-времени с замкнутыми времяподобными кривыми» . Физический обзор D . 42 (6): 1915–1930. Бибкод : 1990PhRvD..42.1915F . дои : 10.1103/PhysRevD.42.1915 . ПМИД 10013039 .
- ^ Торн, Кип; Майкл Моррис; Ульви Юрцевер (1988). «Червоточины, машины времени и слабая энергия» (PDF) . Письма о физических отзывах . 61 (13): 1446–1449. Бибкод : 1988PhRvL..61.1446M . дои : 10.1103/PhysRevLett.61.1446 . ПМИД 10038800 . Архивировано (PDF) из оригинала 9 октября 2022 г.
- ^ Торн, Кип С. (1994). Черные дыры и деформации времени: возмутительное наследие Эйнштейна . WW Нортон. стр. 510 –. ISBN 978-0-393-31276-8 .
Polchinski's paradox.
- ^ Перейти обратно: а б с Торн, Кип С. (1994). Черные дыры и искривления времени . WW Нортон. ISBN 0-393-31276-3 .
- ^ Уилер, Джон; Фейнман, Ричард (1949). «Классическая электродинамика в терминах прямого межчастичного взаимодействия» . Обзоры современной физики . 21 (3): 425–433. Бибкод : 1949РвМП...21..425Вт . дои : 10.1103/RevModPhys.21.425 .
- ^ Эчеверрия, Фернандо; Гуннар Клинкхаммер; Кип Торн (1991). «Бильярдные шары в пространстве-времени-червоточине с замкнутыми времяподобными кривыми: Классическая теория» . Физический обзор D . 44 (4): 1077–1099. Бибкод : 1991PhRvD..44.1077E . дои : 10.1103/PhysRevD.44.1077 . ПМИД 10013968 .
- ^ Перейти обратно: а б с Эрман, Джон (1995). Удары, хруст, всхлипы и визги: особенности и акаузалии в релятивистском пространстве-времени . Издательство Оксфордского университета. ISBN 0-19-509591-Х .
- ^ Нахин, Пол Дж. (1999). Машины времени: путешествия во времени в физике, метафизике и научной фантастике . Американский институт физики. п. 508. ИСБН 0-387-98571-9 .
- ^ Уиллер, Дж. Крейг (2007). Космические катастрофы: взрывающиеся звезды, черные дыры и картирование Вселенной (2-е изд.). Издательство Кембриджского университета. стр. 294–295. ISBN 978-0521857147 .
- ^ Моравец, Ганс (1991). «Путешествие во времени и вычисления» . Архивировано из оригинала 29 января 2009 г. Проверено 28 июля 2008 г.
- ^ Перейти обратно: а б Дойч, Дэвид (1991). «Квантовая механика вблизи замкнутых времениподобных линий» . Физический обзор D . 44 (10): 3197–3217. Бибкод : 1991PhRvD..44.3197D . дои : 10.1103/PhysRevD.44.3197 . ПМИД 10013776 .
- ^ Ааронсон, Скотт (март 2008 г.). «Пределы квантовых компьютеров» (PDF) . Научный американец . 298 (3): 68–69. Бибкод : 2008SciAm.298c..62A . doi : 10.1038/scientificamerican0308-62 . ПМИД 18357822 . Архивировано (PDF) из оригинала 9 октября 2022 г. - на сайте scottaaronson.com.
- ^ Ааронсон, Скотт; Уотрус, Джон (2009). «Замкнутые времяподобные кривые делают квантовые и классические вычисления эквивалентными» (PDF) . Труды Королевского общества А. 465 (2102): 631–647. arXiv : 0808.2669 . Бибкод : 2009RSPSA.465..631A . дои : 10.1098/rspa.2008.0350 . S2CID 745646 . Архивировано (PDF) из оригинала 9 октября 2022 г. - на сайте scottaaronson.com.
- ^ Рингбауэр, Мартин; Брум, Мэтью А.; Майерс, Кейси Р.; Уайт, Эндрю Г.; Ральф, Тимоти К. (19 июня 2014 г.). «Экспериментальное моделирование замкнутых времениподобных кривых». Природные коммуникации . 5 : 4145. arXiv : 1501.05014 . Бибкод : 2014NatCo...5.4145R . дои : 10.1038/ncomms5145 . ПМИД 24942489 . S2CID 12779043 .
- ^ Толксдорф, Юрген; Верх, Райнер (2018). «Квантовая физика, поля и замкнутые времениподобные кривые: условие D-CTC в квантовой теории поля». Связь в математической физике . 357 (1): 319–351. arXiv : 1609.01496 . Бибкод : 2018CMaPh.357..319T . дои : 10.1007/s00220-017-2943-5 . S2CID 253751446 .
- ^ Толксдорф, Юрген; Верх, Райнер (2021). «Условие D-CTC в общем случае выполняется в классических (неквантовых) статистических системах». Основы физики . 51 (93): 93. arXiv : 1912.02301 . Бибкод : 2021FoPh...51...93T . дои : 10.1007/s10701-021-00496-z . S2CID 208637445 .
- ^ Ллойд, Сет ; Макконе, Лоренцо ; Гарсиа-Патрон, Рауль ; Джованнетти, Витторио ; Сикано, Ютака ; Пирандола, Стефано ; Розема, Ли А .; Дараби, Ардаван ; Судагар, Ясаман ; Шалм, Линден К .; Штейнберг, Эфраим М. (27 января 2011 г.). «Замкнутые времяподобные кривые посредством постселекции: теория и экспериментальная проверка согласованности». Письма о физических отзывах . 106 (4): 040403. arXiv : 1005.2219 . Бибкод : 2011PhRvL.106d0403L . doi : 10.1103/PhysRevLett.106.040403 . ПМИД 21405310 . S2CID 18442086 .
- ^ Ллойд, Сет ; Макконе, Лоренцо ; Гарсиа-Патрон, Рауль ; Джованнетти, Витторио ; Сикано, Ютака (2011). «Квантовая механика путешествия во времени посредством телепортации после выбора». Физический обзор D . 84 (2): 025007.arXiv : 1007.2615 . Бибкод : 2011PhRvD..84b5007L . дои : 10.1103/PhysRevD.84.025007 . S2CID 15972766 .
Внешние ссылки
[ редактировать ]- Представление о прошлом и можем ли мы его изменить? – выступление Новикова
- От червоточины к машине времени: комментарии к гипотезе защиты хронологии Хокинга , в которой также рассматривается принцип самосогласованности Новикова
- Эйнштейн Физика предотвращает парадоксальные путешествия во времени
- Путешествия во времени и современная физика