Круговая симметрия
Эта статья включает список литературы , связанную литературу или внешние ссылки , но ее источники остаются неясными, поскольку в ней отсутствуют встроенные цитаты . ( февраль 2017 г. ) |
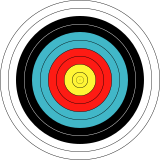 В двухмерном изображении мишень для стрельбы из лука имеет круговую симметрию. |  Поверхность вращения имеет круговую симметрию вокруг оси в трех измерениях. |
В геометрии , круговая симметрия — это тип непрерывной симметрии плоского объекта который можно повернуть на любой произвольный угол и отобразить на себя.
Вращательная круговая симметрия изоморфна группе кругов в комплексной плоскости или специальной ортогональной группе SO (2) и унитарной группе U (1). Рефлексивная круговая симметрия изоморфна ортогональной группе O(2).
Два измерения
[ редактировать ]Двумерный объект с круговой симметрией будет состоять из концентрических кругов и кольцевых областей.
Вращательная круговая симметрия имеет всю циклическую симметрию , Z n как симметрию подгруппы. Рефлексивная круговая симметрия обладает всей двугранной симметрией , Dih n как симметрией подгруппы.
Три измерения
[ редактировать ]
В трехмерном измерении поверхность или тело вращения имеет круговую симметрию вокруг оси, также называемую цилиндрической симметрией или осевой симметрией . Примером может служить прямой круговой конус . Круговая симметрия в трех измерениях имеет всю пирамидальную симметрию , C n v как подгруппы.
, Двойной конус биконус , цилиндр , тороид и сфероид обладают круговой симметрией, а также имеют двустороннюю симметрию, перпендикулярную оси системы (или полуцилиндрическую симметрию ). Эти отражательные круговые симметрии имеют все дискретные призматические симметрии D n h как подгруппы.
Четыре измерения
[ редактировать ]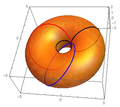 (простой) |  1:5 |  5:1 |
| Цилиндрический | Дуоцилиндрический | |
|---|---|---|
В четырех измерениях объект может иметь круговую симметрию в двух плоскостях ортогональных осей или дуоцилиндрическую симметрию . Например, дуоцилиндр и тор Клиффорда имеют круговую симметрию по двум ортогональным осям. Сфериндер обладает сферической симметрией в одном трехмерном пространстве и круговой симметрией в ортогональном направлении.
Сферическая симметрия
[ редактировать ]
Аналогичный трехмерный эквивалентный термин — сферическая симметрия .
Вращательная сферическая симметрия изоморфна группе вращения SO(3) и может быть параметризована цепочкой вращений Давенпорта по тангажу, рысканию и крену. Вращательная сферическая симметрия имеет все дискретные киральные трехмерные точечные группы как подгруппы. Отражательная сферическая симметрия изоморфна ортогональной группе O(3) и имеет в качестве подгрупп трехмерные дискретные точечные группы.
Скалярное поле имеет сферическую симметрию, если оно зависит только от расстояния до начала координат, например, от потенциала центральной силы . Векторное поле имеет сферическую симметрию, если оно направлено радиально внутрь или наружу с величиной и ориентацией (внутри/наружу). [ нужна ссылка ] в зависимости только от расстояния до начала координат, например, центральная сила.