Классификация Бьянки

В математике классификация Бьянки дает список всех вещественных трехмерных алгебр Ли ( с точностью до изоморфизма ). Классификация содержит 11 классов, 9 из которых содержат одну алгебру Ли, а два из них содержат семейство алгебр Ли континуального размера. (Иногда две группы включаются в бесконечные семейства, что дает 9 классов вместо 11.) Классификация важна в геометрии и физике, поскольку ассоциированные группы Ли служат группами симметрии трехмерных римановых многообразий . Он назван в честь Луиджи Бьянки , который разработал его в 1898 году.

Термин «классификация Бьянки» также используется для аналогичных классификаций в других измерениях и для классификаций комплексных алгебр Ли .

Классификация по размерности менее 3

• Размерность 0: Единственная алгебра Ли — это абелева алгебра Ли R. ⁰ .
• Размерность 1: Единственная алгебра Ли — это абелева алгебра Ли R. ¹ , с внешней группой автоморфизмов - мультипликативной группой ненулевых действительных чисел.
• Размерность 2: существует две алгебры Ли:
  • (1) Абелева алгебра Ли R ² , с внешней группой автоморфизмов GL ₂ ( R ) .
  • (2) Разрешимая алгебра Ли верхнетреугольных матриц размера 2 × 2 со следом 0. Она имеет тривиальный центр и тривиальную внешнюю группу автоморфизмов. Соответствующая . односвязная группа Ли является аффинной группой прямой

Классификация по размеру 3

Все трехмерные алгебры Ли, кроме типов VIII и IX, можно построить как произведение R полупрямое ² и R , где R действует на R ² некоторой матрицей M 2 на 2 . Разные типы соответствуют разным типам матриц M , как описано ниже.

• Тип I : это абелева и унимодулярная алгебра Ли R. ³ . Односвязная группа имеет центр R ³ и внешняя группа автоморфизмов GL ₃ ( R ). Это тот случай, когда М равно 0.
• Тип II : Алгебра Гейзенберга , нильпотентная и унимодулярная. Односвязная группа имеет центр R и внешнюю группу автоморфизмов GL ₂ ( R ). Это тот случай, когда M нильпотентен, но не равен 0 (все собственные значения равны 0).
• Тип III : Эта алгебра является продуктом R и двумерной неабелевой алгебры Ли. (Это предельный случай типа VI, когда одно собственное значение обращается в ноль.) Он разрешим и не унимодулярен. Односвязная группа имеет центр R и внешнюю группу автоморфизмов - группу ненулевых действительных чисел. Матрица M имеет одно нулевое и одно ненулевое собственное значение.
• Тип IV : Алгебра, порожденная [ y , z ] = 0, [ x , y ] = y , [ x , z ] = y + z . Она разрешима и не унимодулярна. Односвязная группа имеет тривиальный центр и внешнюю группу автоморфизмов, состоящую из произведения действительных чисел и группы порядка 2. Матрица M имеет два равных ненулевых собственных значения, но не является диагонализуемой .
• Тип V : [ y , z ] знак равно 0, [ x , y ] знак равно y , [ x , z ] = z . Разрешимая и не унимодулярная. (Предельный случай типа VI, когда оба собственных значения равны.) Односвязная группа имеет тривиальный центр и внешнюю группу автоморфизмов, состоящую из элементов GL ₂ ( R ) определителя +1 или −1. Матрица M имеет два равных собственных значения и диагонализуема.
• Тип VI : Бесконечное семейство: полупрямые произведения R. ² на R , где матрица M имеет ненулевые различные действительные собственные значения с ненулевой суммой. Алгебры разрешимы и не унимодулярны. Односвязная группа имеет тривиальный центр и внешнюю группу автоморфизмов, являющуюся произведением ненулевых действительных чисел и группы порядка 2.
• Тип VI ₀ : Эта алгебра Ли является полупрямым произведением R ² на R , где R где матрица M имеет ненулевые различные действительные собственные значения с нулевой суммой. Она разрешима и унимодулярна. Это алгебра Ли двумерной группы Пуанкаре , группы изометрий двумерного пространства Минковского . Односвязная группа имеет тривиальный центр и внешнюю группу автоморфизмов, представляющую собой произведение положительных действительных чисел с группой диэдра восьмого порядка.
• Тип VII : Бесконечное семейство: полупрямые произведения R. ² на R , где матрица M имеет недействительные и немнимые собственные значения. Разрешимая и не унимодулярная. Односвязная группа имеет тривиальный центр и внешнюю группу автоморфизмов - ненулевые числа.
• Тип VII ₀ : полупрямое произведение R. ² на R , где матрица M имеет ненулевые мнимые собственные значения. Разрешимая и унимодулярная. Это алгебра Ли группы изометрий плоскости. Односвязная группа имеет центр Z и внешнюю группу автоморфизмов, представляющую собой произведение ненулевых действительных чисел и группу порядка 2.
• Тип VIII : Алгебра Ли sl ₂ ( R ) бесследовых матриц размером 2 на 2, ассоциированная с группой SL ₂ (R) . Он простой и унимодульный. Односвязная группа не является матричной группой; это обозначается ${\overline {{\mbox{SL}}(2,\mathbf {R} )}}$, имеет центр Z , а его внешняя группа автоморфизмов имеет порядок 2.
• Тип IX : Алгебра Ли ортогональной группы O ₃ ( R ). Он обозначается 𝖘𝖔(3) и является простым и унимодулярным. Соответствующая односвязная группа — это SU(2) ; он имеет центр порядка 2 и тривиальную внешнюю группу автоморфизмов и является спиновой группой .

Классификация трехмерных комплексных алгебр Ли аналогична, за исключением того, что типы VIII и IX становятся изоморфными, а типы VI и VII становятся частью одного семейства алгебр Ли.

Связные трехмерные группы Ли можно классифицировать следующим образом: они являются факторами соответствующей односвязной группы Ли по дискретной подгруппе центра, поэтому их можно прочитать из таблицы выше.

Терстона Группы связаны с 8 геометриями гипотезы геометризации . Точнее, семь из восьми геометрий могут быть реализованы как левоинвариантные метрики односвязной группы (иногда более чем одним способом). Геометрия Терстона типа S ² × R не может быть реализовано таким образом.

Структурные константы

Каждое трехмерное пространство Бьянки допускает набор из трех векторных полей Киллинга. $\xi _{i}^{(a)}$ которые подчиняются следующему свойству:

$\left({\frac {\partial \xi _{i}^{(c)}}{\partial x^{k}}}-{\frac {\partial \xi _{k}^{(c)}}{\partial x^{i}}}\right)\xi _{(a)}^{i}\xi _{(b)}^{k}=C_{\ ab}^{c}$

где $C_{\ ab}^{c}$, «структурные константы» группы, образуют постоянный тензор третьего порядка, антисимметричный по двум нижним индексам. Для любого трехмерного пространства Бьянки $C_{\ ab}^{c}$ задается отношением

$C_{\ ab}^{c}=\varepsilon _{abd}n^{cd}-\delta _{a}^{c}a_{b}+\delta _{b}^{c}a_{a}$

где $\varepsilon _{abd}$ это символ Леви-Чивита , $\delta _{a}^{c}$ – дельта Кронекера , а вектор $a_{a}=(a,0,0)$ и диагональный тензор $n^{cd}$ описываются следующей таблицей, где $n^{(i)}$ дает i -е собственное значение $n^{cd}$; параметр a пробегает все положительные действительные числа :

Тип Бьянки	$a$	$n^{(1)}$	$n^{(2)}$	$n^{(3)}$	сорт	примечания	графический (рис. 1)
я	0	0	0	0	А	описывает евклидово пространство	в начале
II	0	1	0	0	А		интервал [0,1] вдоль $n^{(1)}$
III	1	0	1	-1	Б	подслучай типа VI а с $a=1$	проецируется в четвертый квадрант плоскости a = 0
IV	1	0	0	1	Б		вертикальное открытое лицо между первым и четвертым квадрантами плоскости a = 0
V	1	0	0	0	Б	имеет гипер- псевсферу как частный случай	интервал (0,1] вдоль оси a
ВИ 0	0	1	-1	0	А		четвертый квадрант горизонтальной плоскости
С помощью	$a$	0	1	-1	Б	когда $a=1$, эквивалентный типу III	проецируется в четвертый квадрант плоскости a = 0
VII 0	0	1	1	0	А	имеет евклидово пространство как особый случай	первый квадрант горизонтальной плоскости
7 век	$a$	0	1	1	Б	имеет гиперпсевдосферу как частный случай	проецируется в первый квадрант плоскости a = 0
VIII	0	1	1	-1	А		шестой октант
IX	0	1	1	1	А	имеет гиперсферу как частный случай	второй октант

Рис. 1. Пространство параметров как 3-плоскость (класс A) и ортогональная полу3-плоскость (класс B) в R ⁴ с координатами ( n ⁽¹⁾ , н ⁽²⁾ , н ⁽³⁾ , а ), показывающие канонических представителей каждого типа Бьянки.

Стандартную классификацию Бьянки можно вывести из структурных констант за следующие шесть шагов:

1. Из-за антисимметрии $C_{ab}^{c}=-C_{ba}^{c}$, существует девять независимых констант $C_{ab}^{c}$. Их можно эквивалентно представить девятью компонентами произвольной постоянной матрицы C ^аб :
   $C_{ab}^{c}=\varepsilon _{abd}C^{dc},$
   где ε _abd — полностью антисимметричный трехмерный символ Леви-Чивита (ε ₁₂₃ = 1). Замена этого выражения на $C_{ab}^{c}$ в тождество Якоби , приводит к
   $\varepsilon _{abd}C^{bd}C^{ac}=0.$
2. Структурные константы можно преобразовать как:
   $C^{ab}=\left(\det {A}\right)^{-1}A_{m}^{a}A_{n}^{b}{\acute {C}}^{mn}.$
   Появление det A в этой формуле связано с тем, что символ ε _abd преобразуется как тензорная плотность: $\varepsilon _{abc}=\left(\det {A}\right)D_{a}^{m}D_{b}^{n}D_{c}^{d}{\acute {\varepsilon }}_{mnd}$, где έ _mnd ≡ ε _mnd . Данным преобразованием всегда можно уменьшить матрицу C ^аб в форму:
   $C^{ab}={\begin{bmatrix}n_{1}&0&0\\0&C^{22}&C^{23}\\0&C^{32}&C^{33}\end{bmatrix}}.$
   После такого выбора сохраняется свобода триадных преобразований, но с ограничениями $A_{2}^{1}=A_{3}^{1}=0$ и $A_{1}^{2}=A_{1}^{3}=0.$
3. Теперь тождества Якоби дают только одно ограничение:
   $\left(C^{23}-C^{32}\right)n_{1}=0.$
4. Если n ₁ ≠ 0, то C ²³ – С ³² = 0 и остальными преобразованиями с $A_{\bar {b}}^{\bar {a}}\neq 0,\quad {\bar {a}},{\bar {b}}={\bar {2}},{\bar {3}}$, матрица 2 × 2 $C^{{\bar {a}}{\bar {b}}}$ в С ^аб можно сделать диагонально. Затем
   $C^{ab}={\begin{bmatrix}n_{1}&0&0\\0&n_{2}&0\\0&0&n_{3}\end{bmatrix}}.$
   Условие диагонали для C ^аб сохраняется при преобразованиях с диагональю $A_{b}^{a}$. При этих преобразованиях три параметра n ₁ , n ₂ , n ₃ изменяются следующим образом:
   $n_{a}=\left(A_{1}^{1}A_{2}^{2}A_{3}^{3}\right)\left(A_{a}^{a}\right)^{2}{\acute {n}}_{a},{\text{no summation over}}\ a.$
   С помощью этих диагональных преобразований модуль любого n _a (если он не равен нулю) можно сделать равным единице. Учитывая, что одновременная смена знака всех n _a не дает ничего нового, приходим к следующим инвариантно различным наборам чисел n ₁ , n ₂ , n ₃ (инвариантно различным в том смысле, что невозможно перейти от друг к другу путем некоторой трансформации триады $e_{a}^{\bar {a}}=A_{\bar {b}}^{\bar {a}}e_{a}^{\bar {b}}$), то есть к следующим различным типам однородных пространств с диагональной матрицей C ^аб :
   ${\begin{matrix}Bianchi\ IX&:&(n_{1},n_{2},n_{3})&=&(1,1,1),\\Bianchi\ VIII&:&(n_{1},n_{2},n_{3})&=&(1,1,-1),\\Bianchi\ VII_{0}&:&(n_{1},n_{2},n_{3})&=&(1,1,0),\\Bianchi\ VI_{0}&:&(n_{1},n_{2},n_{3})&=&(1,-1,0),\\Bianchi\ II&:&(n_{1},n_{2},n_{3})&=&(1,0,0).\end{matrix}}$
5. Рассмотрим теперь случай n ₁ = 0. В этом случае также может случиться, что C ²³ – С ³² = 0. Это возвращается к ситуации, уже проанализированной на предыдущем шаге, но с дополнительным условием n ₁ = 0. Теперь все существенно разные типы для множеств n ₁ , n ₂ , n ₃ равны (0, 1, 1), (0, 1, −1), (0, 0, 1) и (0, 0, 0). Первые три повторяют типы VII ₀ , VI ₀ , II . Следовательно, возникает только один новый тип:
   $Bianchi\ I\ :\ (n_{1},n_{2},n_{3})\ =\ (0,0,0).$
6. Остается только случай n ₁ = 0 и C ²³ – С ³² ≠ 0. Теперь матрица 2 × 2 $C^{{\bar {a}}{\bar {b}}}({\bar {a}},{\bar {b}}=2,3)$ несимметричен и его нельзя сделать диагональным преобразованиями с помощью $A_{\bar {b}}^{\bar {a}}\neq 0$. Однако ее симметричную часть можно диагонализовать, то есть матрицу C 3 × 3 ^аб можно свести к виду:
   $C^{ab}={\begin{bmatrix}0&0&0\\0&n_{2}&a\\0&-a&n_{3}\end{bmatrix}},$
   где а — произвольное число. После этого остается возможность выполнять преобразования с диагональю $A_{\bar {b}}^{\bar {a}}$, при котором величины n ₂ , n ₃ и изменяются следующим образом:
   $n_{2}=\left(A_{1}^{1}A_{2}^{2}A_{3}^{3}\right)^{-1}\left(A_{2}^{2}\right)^{2}{\acute {n}}_{2},\quad n_{3}=\left(A_{1}^{1}A_{2}^{2}A_{3}^{3}\right)^{-1}\left(A_{3}^{3}\right)^{2}{\acute {n}}_{3},\quad a=\left(A_{1}^{1}\right)^{-1}{\acute {a}}.$
   Эти формулы показывают, что для ненулевых n ₂ , n ₃ , a комбинация a ² ( п ₂ п ₃ ) ⁻¹ является инвариантной величиной. По выбору $A_{1}^{1}$, можно наложить условие a > 0 и после этого выбор знака $A_{3}^{3}\left(A_{2}^{2}\right)^{-1}$ позволяет одновременно менять оба знака n ₂ и n ₃ , то есть набор ( n ₂ , n ₃ ) эквивалентен множеству (− n ₂ , − n ₃ ). Отсюда следует, что существуют следующие четыре различных возможности:
   $(a,n_{2},n_{3})=(a,0,0),(a,0,1),(a,1,1),(a,1,-1).$
   Для первых двух число а можно преобразовать в единицу выбором
   параметры $A_{1}^{1}$ и $A_{3}^{3}\left(A_{2}^{2}\right)^{-1}$. Для вторых двух возможностей оба этих параметра уже фиксированы, и а остается инвариантным и произвольным положительным числом. Исторически эти четыре типа однородных пространств были классифицированы как:
   ${\begin{matrix}Bianchi\ V&:&n_{1}=0,\ (a,n_{2},n_{3})&=&(1,0,0),\\Bianchi\ IV&:&n_{1}=0,\ (a,n_{2},n_{3})&=&(1,0,1),\\Bianchi\ VII&:&n_{1}=0,\ (a,n_{2},n_{3})&=&(a,1,1),\\Bianchi\ III&:&n_{1}=0,\ (a,n_{2},n_{3})&=&(1,1,-1),\\Bianchi\ VI&:&n_{1}=0,\ (a,n_{2},n_{3})&=&(a,1,-1).\end{matrix}}$
   Тип III является лишь частным случаем типа VI, соответствующего a = 1. Типы VII и VI содержат бесконечное множество инвариантно различных типов алгебр, соответствующих произвольности непрерывного параметра a . Тип VII ₀ является частным случаем VII, соответствующим a = 0, тогда как тип VI ₀ является частным случаем VI, соответствующим также a = 0.

пространств

Пространства Бьянки обладают тем свойством, что их тензоры Риччи можно разделить на произведение базисных векторов, связанных с пространством, и тензора, не зависящего от координат.

Для заданного показателя :

$ds^{2}=\gamma _{ab}\xi _{i}^{(a)}\xi _{k}^{(b)}dx^{i}dx^{k}$

(где $\xi _{i}^{(a)}dx^{i}$ являются 1-формами ), тензор кривизны Риччи $R_{ik}$ дается:

$R_{ik}=R_{(a)(b)}\xi _{i}^{(a)}\xi _{k}^{(b)}$

$R_{(a)(b)}={\frac {1}{2}}\left[C_{\ \ b}^{cd}\left(C_{cda}+C_{dca}\right)+C_{\ cd}^{c}\left(C_{ab}^{\ \ d}+C_{ba}^{\ \ d}\right)-{\frac {1}{2}}C_{b}^{\ cd}C_{acd}\right]$

где индексы структурных констант повышаются и понижаются с $\gamma _{ab}$ что не является функцией $x^{i}$.

Космологическое применение

В космологии эта классификация используется для однородного пространства-времени размерности 3+1. Трехмерная группа Ли представляет собой группу симметрии трехмерного пространственноподобного среза, а метрика Лоренца, удовлетворяющая уравнению Эйнштейна, генерируется путем изменения компонентов метрики в зависимости от t. Метрики Фридмана –Леметра–Робертсона–Уокера изотропны и представляют собой частные случаи типов I, V, $\scriptstyle {\text{VII}}_{h}$ и IX. Модели Бьянки типа I включают метрику Каснера как особый случай.Космологии Бьянки IX включают метрику Тауба . Однако динамика вблизи сингулярности приближенно определяется серией последовательных периодов Каснера (Бьянки I). Сложная динамика,который по сути представляет собой бильярдное движение в части гиперболического пространства, демонстрирует хаотическое поведение и называется Mixmaster ; его анализ называется анализом БКЛ по имени Белинского, Халатникова и Лифшица. Более поздние работы установили связь теорий (супер)гравитации вблизи пространственноподобной особенности (BKL-предела) с лоренцевыми алгебрами Каца–Муди , группами Вейля и гиперболическими группами Кокстера . Другая более поздняя работа посвящена дискретному характеру отображения Каснера и непрерывному обобщению. В пространстве одновременно однородном и изотропном метрика определяется полностью, оставляя свободным только знак кривизны. Предполагая только однородность пространства без дополнительной симметрии, такой как изотропия, оставляет значительно больше свободы в выборе метрики. Следующее относится к пространственной части метрики в данный момент времени t, предполагая синхронный кадр, так что t является одним и тем же синхронизированным временем для всего пространства.

Однородность предполагает одинаковые метрические свойства во всех точках пространства. Точное определение этого понятия предполагает рассмотрение наборов преобразований координат, которые преобразуют пространство в себя, т.е. оставляют его метрику неизменной: если линейный элемент до преобразования

$dl^{2}=\gamma _{\alpha \beta }\left(x^{1},x^{2},x^{3}\right)dx^{\alpha }dx^{\beta },$

то после преобразования тот же элемент строки будет

$dl^{2}=\gamma _{\alpha \beta }\left(x^{\prime 1},x^{\prime 2},x^{\prime 3}\right)dx^{\prime \alpha }dx^{\prime \beta },$

с той же функциональной зависимостью γαβ _от новых координат. (Более теоретическое и независимое от координат определение однородного пространства см. в разделе « Гомогенное пространство »). Пространство является однородным, если оно допускает набор преобразований ( группу движений ), приводящих любую данную точку в положение любой другой точки. Поскольку пространство трехмерно, различные преобразования группы помечены тремя независимыми параметрами.

Рисунок 2. Триада e ^{( а )} ( и ⁽¹⁾ , и ⁽²⁾ , и ⁽³⁾ ) — аффинная система координат (в том числе в частном случае декартова система координат), координаты которой являются функциями криволинейных координат x _α (x ₁ , x ₂ , x ₃ ).

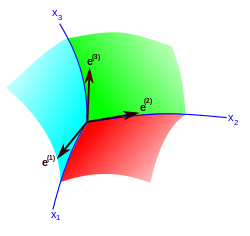
В евклидовом пространстве однородность пространства выражается инвариантностью метрики относительно параллельных смещений ( трансляций ) декартовой системы координат . Каждый перенос определяется тремя параметрами — компонентами вектора смещения начала координат. Все эти преобразования оставляют неизменными три независимых дифференциала ( dx , dy , dz ), из которых строится линейный элемент. В общем случае неевклидова однородного пространства преобразования его группы движений вновь оставляют инвариантными три независимые линейные дифференциальные формы , которые, однако, не сводятся к полным дифференциалам каких-либо координатных функций. Эти формы записываются как $e_{\alpha }^{(a)}dx^{\alpha }$ где латинский индекс ( а ) обозначает три независимых вектора (координатных функции); эти векторы называются полем кадра или триадой. Греческие буквы обозначают три пространственно-подобные криволинейные координаты . Пространственный метрический инвариант строится относительно заданной группы движений с использованием приведенных выше форм:

$dl^{2}=\eta _{ab}\left(e_{\alpha }^{(a)}dx^{\alpha }\right)\left(e_{\beta }^{(b)}dx^{\beta }\right)$ ( уравнение 6а )

т.е. метрический тензор

$\gamma _{\alpha \beta }=\eta _{ab}e_{\alpha }^{(a)}e_{\beta }^{(b)}$ ( уравнение 6b )

где коэффициенты ηab _, симметричные по индексам a и b , являются функциями времени. Выбор базисных векторов продиктован свойствами симметрии пространства, и, вообще говоря, эти базисные векторы не ортогональны (так что матрица η _ab не диагональна).

Обратная тройка векторов $e_{(a)}^{\alpha }$ вводится с помощью дельты Кронекера

$e_{(a)}^{\alpha }e_{\alpha }^{(b)}=\delta _{a}^{b};\quad e_{(a)}^{\alpha }e_{\beta }^{(a)}=\delta _{\alpha }^{\beta }$ ( уравнение 6c )

В трехмерном случае связь между двумя векторными тройками можно записать явно

$\mathbf {e} _{(1)}={\frac {1}{v}}\mathbf {e} ^{(2)}\times \mathbf {e} ^{(3)},\quad \mathbf {e} _{(2)}={\frac {1}{v}}\mathbf {e} ^{(3)}\times \mathbf {e} ^{(1)},\quad \mathbf {e} _{(3)}={\frac {1}{v}}\mathbf {e} ^{(1)}\times \mathbf {e} ^{(2)},$ ( уравнение 6d )

объем v где

$v=\left\vert e_{\alpha }^{(a)}\right\vert =\mathbf {e} ^{(1)}\cdot \mathbf {e} ^{(2)}\times \mathbf {e} ^{(3)},$

с е _{( а )} и е ^{( а )} рассматриваются как декартовы векторы с компонентами $e_{(a)}^{\alpha }$ и $e_{\alpha }^{(a)}$, соответственно. Определитель ( метрического тензора ур. 6б есть γ = η v ² где η — определитель матрицы η _ab .

Требуемые условия однородности пространства:

$\left({\frac {\partial e_{\alpha }^{(c)}}{\partial x^{\beta }}}-{\frac {\partial e_{\beta }^{(c)}}{\partial x^{\alpha }}}\right)e_{(a)}^{\alpha }e_{(b)}^{\beta }=C_{ab}^{c}.$ ( уравнение 6e )

Константы $C_{ab}^{c}$ называются структурными константами группы.

showДоказательство уравнения. 6е

The invariance of the differential forms $e_{\alpha }^{(a)}dx^{\alpha }$ means that $e_{\alpha }^{(a)}(x)dx^{\alpha }=e_{\alpha }^{(a)}(x^{\prime })dx^{\prime \alpha }$ where the $e_{\alpha }^{(a)}$ on the two sides of the equation are the same functions of the old and new coordinates, respectively. Multiplying this equation by $e_{(a)}^{\beta }(x^{\prime })$, setting $dx^{\prime \beta }={\frac {\partial x^{\prime \beta }}{\partial x^{\alpha }}}dx^{\alpha },$ and comparing coefficients of the same differentials dxα, one finds ${\frac {\partial x^{\prime \beta }}{\partial x^{\alpha }}}=e_{(a)}^{\beta }(x^{\prime })e_{\alpha }^{(a)}(x).$ These equations are a system of differential equations that determine the functions $x^{\prime \beta }(x)$ for a given frame. In order to be integrable, these equations must satisfy identically the conditions ${\frac {\partial ^{2}x^{\prime \beta }}{\partial x^{\alpha }\partial x^{\gamma }}}={\frac {\partial ^{2}x^{\prime \beta }}{\partial x^{\gamma }\partial x^{\alpha }}}.$ Calculating the derivatives, one finds $\left[{\frac {\partial e_{(a)}^{\beta }(x^{\prime })}{\partial x^{\prime \delta }}}e_{(b)}^{\delta }(x^{\prime })-{\frac {\partial e_{(b)}^{\beta }(x^{\prime })}{\partial x^{\prime \delta }}}e_{(a)}^{\delta }(x^{\prime })\right]e_{\gamma }^{(b)}(x)e_{\alpha }^{(a)}(x)=e_{(a)}^{\beta }(x^{\prime })\left[{\frac {\partial e_{\gamma }^{(a)}(x)}{\partial x^{\alpha }}}-{\frac {\partial e_{\alpha }^{(a)}(x)}{\partial x^{\gamma }}}\right].$ Multiplying both sides of the equations by $e_{(d)}^{\alpha }(x)e_{(c)}^{\gamma }(x)e_{\beta }^{(f)}(x^{\prime })$ and shifting the differentiation from one factor to the other by using eq. 6c, one gets for the left side: $e_{\beta }^{(f)}(x^{\prime })\left[{\frac {\partial e_{(d)}^{\beta }(x^{\prime })}{\partial x^{\prime \delta }}}e_{(c)}^{\delta }(x^{\prime })-{\frac {\partial e_{(c)}^{\beta }(x^{\prime })}{\partial x^{\prime \delta }}}e_{(d)}^{\delta }(x^{\prime })\right]=e_{(c)}^{\beta }(x^{\prime })e_{(d)}^{\delta }(x^{\prime })\left[{\frac {\partial e_{\beta }^{(f)}(x^{\prime })}{\partial x^{\prime \delta }}}-{\frac {\partial e_{\delta }^{(f)}(x^{\prime })}{\partial x^{\prime \beta }}}\right].$ and for the right, the same expression in the variable x. Since x and x' are arbitrary, these expression must reduce to constants to obtain eq. 6e.

Умножение на $e_{(c)}^{\gamma }$, экв. 6e можно переписать в виде

$e_{(a)}^{\alpha }{\frac {\partial e_{(b)}^{\gamma }}{\partial x^{\alpha }}}-e_{(b)}^{\beta }{\frac {\partial e_{(a)}^{\gamma }}{\partial x^{\beta }}}=C_{ab}^{c}e_{(c)}^{\gamma }.$ ( уравнение 6f )

Уравнение 6e можно записать в векторной форме как

$\mathbf {e} _{(a)}\times \mathbf {e} _{(b)}{\text{curl }}\mathbf {e} ^{(c)}=-C_{ab}^{c},$

где снова векторные операции выполняются так, как если бы координаты x ^а были картезианскими. Используя уравнение. 6d , получаем

${\frac {1}{v}}\left(\mathbf {e} ^{(1)}{\text{curl }}\mathbf {e} ^{(1)}\right)=C_{32}^{1},\quad {\frac {1}{v}}\left(\mathbf {e} ^{(2)}{\text{curl }}\mathbf {e} ^{(1)}\right)=C_{13}^{1},\quad {\frac {1}{v}}\left(\mathbf {e} ^{(3)}{\text{curl }}\mathbf {e} ^{(1)}\right)=C_{21}^{1}$ ( уравнение 6g )

и еще шесть уравнений, полученных циклической перестановкой индексов 1, 2, 3.

Структурные константы антисимметричны по своим нижним индексам, как видно из уравнения их определения. 6е : $C_{ab}^{c}=-C_{ba}^{c}$. Другое условие на структурные константы можно получить, заметив, что уравнение. 6f можно записать в виде коммутационных соотношений

$\left[X_{a},X_{b}\right]\equiv X_{a}X_{b}-X_{b}X_{a}=C_{ab}^{c}X_{c}$ ( уравнение 6h )

для линейных дифференциальных операторов

$X_{a}=e_{(a)}^{\alpha }{\frac {\partial }{\partial x^{\alpha }}}$ ( уравнение 6i )

В математической теории непрерывных групп ( групп Ли ) операторы Xa, _уравн удовлетворяющие условиям . 6h называются образующими группы . Теория групп Ли использует операторы, определенные с помощью векторов Киллинга. $\xi _{(a)}^{\alpha }$ вместо триад $e_{(a)}^{\alpha }$. Поскольку в синхронной метрике ни одна из компонент γαβ не _{зависит} от времени, векторы Киллинга (триады) времениподобны.

Условия уравнения 6h следует из тождества Якоби

$[[X_{a},X_{b}],X_{c}]+[[X_{b},X_{c}],X_{a}]+[[X_{c},X_{a}],X_{b}]=0$

и иметь форму

$C_{ab}^{e}C_{ec}^{d}+C_{bc}^{e}C_{ea}^{d}+C_{ca}^{e}C_{eb}^{d}=0$ ( уравнение 6j )

Определенным преимуществом является использование вместо трехиндексных констант $C_{ab}^{c}$, набор двухиндексных величин, полученный двойственным преобразованием

$C_{ab}^{c}=e_{abd}C^{dc}$ ( уравнение 6k )

где е _abc = е ^абв — единичный антисимметричный символ (при e ₁₂₃ = +1). С этими константами коммутационные соотношения уравн. 6h записываются как

$e^{abc}X_{b}X_{c}=C^{ad}X_{d}$ ( уравнение 6l )

Свойство антисимметрии уже учтено в уравнении определения. 6к , в то время как экв. 6j принимает вид

$e_{bcd}C^{cd}C^{ba}=0$ ( экв. 6м )

Выбор трех векторов системы отсчёта в дифференциальных формах $e_{\alpha }^{(a)}dx^{\alpha }$ (а вместе с ними и операторы X _a ) не единственен. Их можно подвергнуть любому линейному преобразованию с постоянными коэффициентами:

$\mathbf {e} _{(a)}=A_{a}^{b}\mathbf {e} _{(b)}.$ ( уравнение 6n )

Величины η _ab и C ^аб ведут себя как тензоры (инвариантны) относительно таких преобразований.

Условия уравнения 6m — единственные, которым должны удовлетворять структурные константы. Но среди констант, допустимых этими условиями, есть эквивалентные множества в том смысле, что их отличие связано с преобразованием типа ур. 6н . Вопрос классификации однородных пространств сводится к определению всех неэквивалентных наборов структурных констант. Это можно сделать, используя «тензорные» свойства величин C ^аб , следующим простым методом (К.Г. Бер, 1962).

Асимметричный тензор C ^аб можно разделить на симметричную и антисимметричную часть. Первый обозначается n ^аб , а второй выражается через его двойственный вектор a _c :

$C^{ab}=n^{ab}+e^{abc}a_{c}.$ ( уравнение 6o )

Подстановка этого выражения в уравн. 6m приводит к условию

$n^{ab}a_{b}=0.$ ( ур. 6p )

С помощью преобразований урав. 6n симметричный тензор n ^аб можно привести к диагональному виду с собственными значениями n ₁ , n ₂ , n ₃ . Уравнение 6p показывает, что вектор a _b (если он существует) лежит вдоль одного из главных направлений тензора n ^аб , соответствующий нулевому собственному значению. Поэтому без ограничения общности можно положить a _b = ( a , 0, 0). Тогда уравнение. 6p сводится к an ₁ = 0, т.е. одна из величин a или n ₁ должна быть равна нулю. Тождества Якоби принимают вид:

$[X_{1},X_{2}]=-aX_{2}+n_{3}X_{3},\quad [X_{2},X_{3}]=n_{1}X_{1},\quad [X_{3},X_{1}]=n_{2}X_{2}+aX_{3}.$ ( уравнение 6q )

операторов Xa _{Единственными оставшимися свободами являются смена знаков} и их умножение на произвольные константы. Это позволяет одновременно изменить знак всех n _a , а также сделать величину положительной (если она отлична от нуля). Также все структурные константы можно сделать равными ±1, если хотя бы одна из величин a , n ₂ , n ₃ обращается в нуль. Но если все три эти величины отличны от нуля, масштабные преобразования оставляют неизменным соотношение h = a ² ( п ₂ п ₃ ) ⁻¹ .

Таким образом, приходим к классификации Бьянки, перечисляющей возможные типы однородных пространств, классифицируемых значениями a , n ₁ , n ₂ , n _3, которая графически представлена ​​на рис. 3. В случае класса A ( a = 0) тип IX ( н ⁽¹⁾ =1, н ⁽²⁾ =1, н ⁽³⁾ =1) представлен октантом 2 типа VIII ( n ⁽¹⁾ =1, н ⁽²⁾ =1, н ⁽³⁾ =–1) представлен октантом 6, а тип VII ₀ ( n ⁽¹⁾ =1, н ⁽²⁾ =1, н ⁽³⁾ =0) представлен первым квадрантом горизонтальной плоскости и типом VI ₀ ( n ⁽¹⁾ =1, н ⁽²⁾ =–1, н ⁽³⁾ =0) представлен четвертым квадрантом этой плоскости; тип II (( n ⁽¹⁾ =1, н ⁽²⁾ =0, н ⁽³⁾ =0) представлен интервалом [0,1] вдоль n ⁽¹⁾ и введите I ( n ⁽¹⁾ =0, н ⁽²⁾ =0, н ⁽³⁾ =0) находится в начале координат. Аналогично и в случае класса B (при n ⁽³⁾ = 0), тип Бьянки VI _h ( a = h , n ⁽¹⁾ =1, н ⁽²⁾ =–1) проецируется в четвертый квадрант горизонтальной плоскости и тип VII _h ( a = h , n ⁽¹⁾ =1, н ⁽²⁾ =1) проецируется в первый квадрант горизонтальной плоскости; эти последние два типа представляют собой единый класс изоморфизма, соответствующий поверхности постоянного значения функции h = a ² ( н ⁽¹⁾ н ⁽²⁾ ) ⁻¹ . Типичная такая поверхность изображена в одном октанте, угол θ определяется формулой tan θ = | ч /2| ^1/2 ; в остальных октантах получаются вращением на кратные π /2, h, чередующиеся по знаку для данной величины | ч |. Тип III является подтипом VI _h с = 1. Тип V ( а =1, n ⁽¹⁾ =0, н ⁽²⁾ =0) — интервал (0,1] по оси а и тип IV ( a =1, n ⁽¹⁾ =1, н ⁽²⁾ =0) — это вертикальная открытая грань между первым и четвертым квадрантами плоскости a = 0, причем последняя дает предел класса A каждого типа.

Уравнения Эйнштейна для Вселенной с однородным пространством можно с помощью поля отсчета свести к системе обыкновенных дифференциальных уравнений, содержащей только функции времени. Для этого необходимо разрешить пространственные компоненты четырехвекторов и четырехтензоров по триаде базисных векторов пространства:

$R_{(a)(b)}=R_{\alpha \beta }e_{(a)}^{\alpha }e_{(b)}^{\beta },\quad R_{0(a)}=R_{0\alpha }e_{(a)}^{\alpha },\quad u^{(a)}=u^{\alpha }e_{\alpha }^{(a)},$

где все эти величины теперь являются функциями только t ; скалярные величины — плотность энергии ε и давление вещества p — также являются функциями времени.

Уравнения Эйнштейна в вакууме в синхронной системе отсчета имеют вид

$R_{0}^{0}=-{\frac {1}{2}}{\frac {\partial \varkappa _{\alpha }^{\alpha }}{\partial t}}-{\frac {1}{4}}\varkappa _{\alpha }^{\beta }\varkappa _{\beta }^{\alpha }=0,$ ( уравнение 11 )

$R_{\alpha }^{\beta }=-{\frac {1}{2{\sqrt {-g}}}}{\frac {\partial }{\partial t}}\left({\sqrt {-g}}\varkappa _{\alpha }^{\beta }\right)-P_{\alpha }^{\beta }=0,$ ( уравнение 12 )

$R_{\alpha }^{0}={\frac {1}{2}}\left(\varkappa _{\alpha ;\beta }^{\beta }-\varkappa _{\beta ;\alpha }^{\beta }\right)=0,$ ( уравнение 13 )

где $\varkappa _{\alpha }^{\beta }$ это трехмерный тензор $\varkappa _{\alpha }^{\beta }={\frac {\partial \gamma _{\alpha }^{\beta }}{\partial t}}$, а P _αβ — трёхмерный тензор Риччи , который выражается трёхмерным метрическим тензором γ _αβ так же, как R _ik выражается через g _ik ; P _αβ содержит только пространственные (но не временные) производные от γ _αβ . Используя триады, для ур. 11 просто есть

$\varkappa _{(a)(b)}={\frac {\partial \eta _{ab}}{\partial t}},\quad \varkappa _{(a)}^{(b)}={\frac {\partial \eta _{ac}}{\partial t}}\eta ^{cb}.$

Компоненты P _{( a )( b )} могут быть выражены через величины η _ab и структурные константы группы, используя тетрадное представление тензора Риччи через величины $\lambda _{abc}=\left(e_{(a)i,k}-e_{(a)k,i}\right)e_{(b)}^{i}e_{(c)}^{k}$

$R_{(a)(b)}=-{\frac {1}{2}}\left(\lambda _{ab,c}^{c}+\lambda _{ba,c}^{c}+\lambda _{ca,b}^{c}+\lambda _{cb,a}^{c}+\lambda _{b}^{cd}\lambda _{cda}+\lambda _{b}^{cd}\lambda _{dca}-{\frac {1}{2}}\lambda _{b}^{cd}\lambda _{acd}+\lambda _{cd}^{c}\lambda _{ab}^{d}+\lambda _{cd}^{c}\lambda _{ba}^{d}\right).$

После замены трехиндексных символов $\lambda _{bc}^{a}=C_{bc}^{a}$ двухиндексными символами C ^аб и преобразования:

$\eta _{ad}\eta _{bc}\eta _{cf}e^{def}=\eta e_{abc},\quad e_{abf}e^{cdf}=\delta _{a}^{c}\delta _{b}^{d}-\delta _{a}^{d}\delta _{b}^{c}$

получается «однородный» тензор Риччи, выраженный в структурных константах:

$P_{(a)}^{(b)}={\frac {1}{2\eta }}\left\{2C^{bd}C_{ad}+C^{db}C_{ad}+C^{bd}C_{da}-C_{d}^{d}\left(C_{a}^{b}+C_{a}^{b}\right)+\delta _{a}^{b}\left[\left(C_{d}^{d}\right)^{2}-2C^{df}C_{df}\right]\right\}.$

Здесь все индексы поднимаются и опускаются с помощью локального метрического тензора η _ab

$C_{a}^{b}=\eta _{ac}C^{cb},\quad C_{ab}=\eta _{ac}\eta _{bd}C^{cd}.$

Тождества Бьянки для трехмерного тензора P _αβ в однородном пространстве принимают вид

$P_{b}^{c}C_{ca}^{b}+P_{a}^{c}C_{cb}^{b}=0.$

С учетом преобразований ковариантных производных для произвольных четырехвекторов A _i и четырехтензоров A _ik

$A_{i;k}e_{(a)}^{i}e_{(b)}^{k}=A_{(a)(b)}-A^{(d)}\gamma _{dab},$

$A_{ik;l}e_{(a)}^{i}e_{(b)}^{k}e_{(c)}^{l}=A_{(a)(b)(c)}-A_{(b)}^{(d)}\gamma _{dac}+A_{(a)}^{(d)}\gamma _{dbc},$

окончательные выражения для компонентов триады четырехтензора Риччи:

$R_{0}^{0}=-{\frac {1}{2}}{\frac {\partial \varkappa _{(a)}^{(a)}}{\partial t}}-{\frac {1}{4}}\varkappa _{(a)}^{(b)}\varkappa _{(b)}^{(a)},$ ( уравнение 11а )

$R_{(a)}^{(b)}=-{\frac {1}{2{\sqrt {\eta }}}}{\frac {\partial }{\partial t}}\left({\sqrt {\eta }}\varkappa _{(a)}^{(b)}\right)-P_{(a)}^{(b)},$ ( уравнение 12а )

$R_{(a)}^{0}=-{\frac {1}{2}}\varkappa _{(b)}^{(c)}\left(C_{ca}^{b}-\delta _{a}^{b}C_{dc}^{d}\right).$ ( уравнение 13а )

Таким образом, при построении уравнений Эйнштейна нет необходимости использовать явные выражения для базисных векторов как функций координат.

См. также

• Таблица групп Ли
• Список простых групп Ли
• БКЛ сингулярность

Библиография

• Белинский Владимир Александрович ; Халатников И.М. ; Лифшиц, Э.М. (1971). «Колебательный режим приближения к сингулярности в однородных космологических моделях с вращающимися осями». ЖЭТФ . 60 (6): 1969–1979.
• Белинский Владимир Александрович ; Халатников И.М. ; Лифшиц, Э.М. (1972). «Построение общего космологического решения уравнения Эйнштейна с особенностью времени». ЖЭТФ . 62 (5): 1606–1613.
• Л. Бьянки, О трехмерных пространствах, допускающих непрерывную группу движений. (О трехмерных пространствах, допускающих непрерывную группу движений.) Soc. Sci di Mat. 11, 267 (1898) английский перевод. Архивировано 18 февраля 2020 г. в Wayback Machine.
• Корниш, Нью-Джерси; Левин, Джей-Джей (1997a). «Вселенная Mixmaster однозначно хаотична». В Пиране Цви; Руффини, Ремо (ред.). О последних разработках в области теоретической и экспериментальной общей теории относительности, гравитации и релятивистской теории поля . Материалы восьмой встречи Марселя Гроссмана. Еврейский университет в Иерусалиме: World Scientific. стр. 616–618. ISBN  978-9810237936 . ОЛ   13168102М .
• Корниш, Нил Дж.; Левин, Жанна Дж. (1997b). «Вселенная Mixmaster хаотична». Письма о физических отзывах . 78 (6): 998–1001. arXiv : gr-qc/9605029 . Бибкод : 1997PhRvL..78..998C . дои : 10.1103/physrevlett.78.998 . ISSN   0031-9007 . S2CID   119476182 .
• Корниш, Нил Дж.; Левин, Жанна Дж. (1997c). «Вселенная Mixmaster: Хаотичная сказка Фей». Физический обзор D . 55 (12). Американское физическое общество (APS): 7489–7510. arXiv : gr-qc/9612066 . Бибкод : 1997PhRvD..55.7489C . дои : 10.1103/physrevd.55.7489 . ISSN   0556-2821 . S2CID   17085583 .
• Феррандо, Джей-Джей; Саез, JA (2020). «Однородные трехмерные римановы пространства». Классическая и квантовая гравитация . 37 (18): 185011. arXiv : 2004.01877 . Бибкод : 2020CQGra..37r5011F . дои : 10.1088/1361-6382/ab9880 . S2CID   214802205 .
• Гвидо Фубини О четырехмерных пространствах, допускающих непрерывную группу движений .) Ann. Мэтт. чистое приложение. (3) 9, 33–90 (1904); перепечатано в Opere Scelte под редакцией Итальянского математического союза и при участии Национального исследовательского совета Roma Edizioni Cremonese, 1957–62.
• МакКаллум, О классификации реальных четырехмерных алгебр Ли , в «На пути Эйнштейна: эссе в честь Энгельберта Шукинга» под редакцией А. Л. Харви, Спрингера. ISBN   0-387-98564-6
• Энно, Марк ; Перссон, Дэниел; Шпиндель, Филипп (2008). «Пространственноподобные особенности и скрытые симметрии гравитации» . Живые обзоры в теории относительности . 11 (1): 1. arXiv : 0710.1818 . Бибкод : 2008LRR....11....1H . дои : 10.12942/lrr-2008-1 . ПМЦ   5255974 . ПМИД   28179821 .
• Энно, Марк ; Перссон, Дэниел; Уэсли, Дэниел (2008). «Групповая структура Кокстера космологического биллиарда на компактных пространственных многообразиях». Журнал физики высоких энергий . 2008 (9): 052. arXiv : 0805.3793 . Бибкод : 2008JHEP...09..052H . дои : 10.1088/1126-6708/2008/09/052 . ISSN   1029-8479 . S2CID   14135098 .
• Энно, Марк (2009). «Алгебры Каца-Муди и структура космологических особенностей: новый взгляд на анализ Белинского-Халатникова-Лифшица». Квантовая механика фундаментальных систем: поиск красоты и простоты . стр. 1–11. arXiv : 0806.4670 . дои : 10.1007/978-0-387-87499-9_11 . ISBN  978-0-387-87498-2 . S2CID   18809715 .
• Роберт Т. Янцен, Классификация 3-геометрий Бьянки: оригинальные статьи в переводе
• Янцен, Роберт Т. (2001). «Пространственно однородная динамика: единая картина». Учеб. Межд. СЧ. Физ. Курс «Э. Ферми» . LXXXVI . arXiv : gr-qc/0102035 .
• Ландау Лев Д. ; Лифшиц, Евгений М. (1988). Классическая теория полей (7-е изд.). Москва: Наука . ISBN  978-5-02-014420-0 . Том. 2 курса теоретической физики
• Лифшиц, Евгений М .; Халатников, Исаак М. (1963). «Проблемы реалистической космологии» . Специальные физические науки . 80 (7): 391–438. дои : 10.3367/УФНр.0080.196307д.0391 . , английский перевод в Лифшиц, Е.М.; Халатников, И. М. (1963). «Проблемы релятивистской космологии». Достижения физики . 12 (46): 185. Бибкод : 1963AdPhy..12..185L . дои : 10.1080/00018736300101283 .
• Райан, Майкл П.; Шепли, Лоуренс К. (1975). Однородные релятивистские космологии . Принстонская серия по физике. Принстон, Нью-Джерси: Издательство Принстонского университета. ISBN  9780691645209 .
• Стефани, Ганс; Крамер, Дитрих; МакКаллум, Малькольм; Хоэнселерс, Корнелиус; Херлт, Эдуард (2003). Точные решения уравнений поля Эйнштейна (второе изд.). Издательство Кембриджского университета. ISBN  978-0-521-46136-8 .
• Уолд, Роберт М. (1984). Общая теория относительности . Чикаго: Издательство Чикагского университета. ISBN  0-226-87033-2 .