Когерентное состояние

В физике , особенно в квантовой механике , когерентное состояние — это особое квантовое состояние квантового гармонического осциллятора , часто описываемое как состояние, динамика которого наиболее близко напоминает колебательное поведение классического гармонического осциллятора . Это был первый пример квантовой динамики , когда Эрвин Шредингер вывел его в 1926 году при поиске решений уравнения Шредингера , удовлетворяющих принципу соответствия . Квантовый гармонический осциллятор (и, следовательно, когерентные состояния) возникают в квантовой теории широкого круга физических систем. Например, когерентное состояние описывает колебательное движение частицы, заключенной в квадратичной потенциальной яме (более раннюю информацию см., например, в Шиффа ). учебнике ). Когерентное состояние описывает состояние в системе, в котором волновой пакет основного состояния смещен от начала координат системы. Это состояние можно отнести к классическим решениям посредством частицы, колеблющейся с амплитудой, эквивалентной смещению.

Эти состояния, выраженные как собственные векторы понижающего оператора и образующие сверхполное семейство, были введены в ранних работах Джона Р. Клаудера , например В квантовой теории света ( квантовой электродинамике ) и других бозонных квантовых теориях поля когерентные состояния были введены в работе Роя Дж. Глаубера в 1963 и известны также как глауберовские состояния .

Концепция когерентных состояний была значительно абстрагирована; это стало основной темой в математической физике и прикладной математике с приложениями, варьирующимися от квантования до обработки сигналов и обработки изображений (см. Когерентные состояния в математической физике ). По этой причине когерентные состояния, связанные с квантовым гармоническим осциллятором, иногда называют каноническими когерентными состояниями (CCS), стандартными когерентными состояниями , гауссовскими состояниями или состояниями осцилляторов.

Когерентные состояния в квантовой оптике

Рисунок 1: Электрическое поле, измеренное методом оптического гомодинного обнаружения , как функция фазы для трех когерентных состояний, излучаемых Nd:YAG-лазером. Величина квантового шума в электрическом поле совершенно не зависит от фазы. По мере увеличения напряженности поля, т.е. амплитуды колебаний α когерентного состояния, квантовый шум или неопределенность постоянны и составляют 1/2, и поэтому становятся все менее и менее значимыми. В пределе большого поля состояние становится хорошим приближением бесшумной устойчивой классической волны. Среднее число фотонов трех состояний сверху вниз составляет ⟨n⟩ =4,2, 25,2, 924,5.

Рисунок 2: Осциллирующий волновой пакет, соответствующий второму когерентному состоянию, изображенному на рисунке 1. На каждой фазе светового поля распределение представляет собой гауссово уравнение постоянной ширины.

Рисунок 3: Функция Вигнера когерентного состояния, изображенная на рисунке 2. Распределение сосредоточено на амплитуде состояния α и симметрично относительно этой точки . Рябь возникает из-за экспериментальных ошибок.

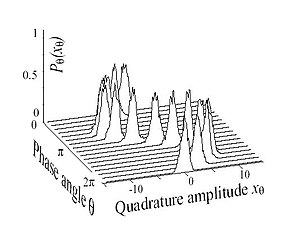
В квантовой оптике когерентным состоянием называют состояние квантованного электромагнитного поля и т. д. который описывает максимальный вид связности и классический вид поведения. Эрвин Шредингер вывел его как «минимальной неопределенности » гауссов волновой пакет в 1926 году, ища решения уравнения Шрёдингера , удовлетворяющие принципу соответствия . Это состояние минимальной неопределенности , при котором единственный свободный параметр выбран так, чтобы относительная дисперсия (стандартное отклонение в натуральных безразмерных единицах) была одинаковой для положения и импульса, каждый из которых одинаково мал при высокой энергии.

Далее, в отличие от энергетических собственных состояний системы, временная эволюция когерентного состояния сосредоточена вдоль классических траекторий . Квантовый линейный гармонический осциллятор и, следовательно, когерентные состояния возникают в квантовой теории широкого круга физических систем. Они встречаются в квантовой теории света ( квантовой электродинамике ) и других бозонных квантовых теориях поля .

Хотя гауссовы волновые пакеты с минимальной неопределенностью были хорошо известны, они не привлекали полного внимания до тех пор, пока Рой Дж. Глаубер в 1963 году не предоставил полное квантово-теоретическое описание когерентности в электромагнитном поле. одновременный вклад ЭКГ Сударшана . В этом отношении не следует упускать из виду (однако в статье Глаубера есть примечание, которое гласит: «Использование этих состояний в качестве производящих функций для $n$-квантовые состояния, однако, были созданы Дж. Швингером. ).Глауберу было предложено сделать это, чтобы предоставить описание эксперимента Хэнбери-Брауна и Твисса с очень широкой базовой линией (сотни или тысячи миль) , в результате которого были получены интерференционные картины , которые можно было использовать для определения диаметров звезд. Это открыло дверь к гораздо более полному пониманию когерентности. (Подробнее см. Квантовомеханическое описание .)

В классической оптике свет рассматривается как электромагнитные волны, исходящие от источника. Часто когерентный лазерный свет рассматривают как свет, излучаемый множеством таких источников, находящихся в синфазной фазе . На самом деле, представление о том, что один фотон находится в фазе с другим, не соответствует квантовой теории. Лазерное излучение создается в резонансной полости , где резонансная частота полости такая же, как частота, связанная с переходами атомных электронов, обеспечивающими поток энергии в поле. По мере накопления энергии в резонансном режиме вероятность вынужденного излучения только в этом режиме увеличивается. Это петля положительной обратной связи , в которой амплитуда в резонансном режиме увеличивается экспоненциально , пока некоторые нелинейные эффекты не ограничивают ее. В качестве контрпримера: лампочка излучает свет в континууме режимов, и нет ничего, что отдавало бы предпочтение одному режиму над другим. Процесс излучения весьма случайен в пространстве и времени (см. тепловой свет ). Однако в лазере свет излучается в резонансном режиме, и этот режим очень важен. последовательный . Таким образом, лазерный свет идеализируется как когерентное состояние. (Классически мы описываем такое состояние электрическим полем, колеблющимся как устойчивая волна. См. рис. 1.)

Помимо описания лазеров, когерентные состояния также ведут себя удобным образом при описании квантового действия светоделителей : два входных луча в когерентном состоянии просто преобразуются в два луча в когерентном состоянии на выходе с новыми амплитудами, заданными классическими формулами электромагнитных волн; такого простого поведения не происходит для других входных состояний, включая числовые состояния. Аналогично, если луч света в когерентном состоянии частично поглощается, то остаток представляет собой чистое когерентное состояние с меньшей амплитудой, тогда как частичное поглощение света в некогерентном состоянии создает более сложное статистическое смешанное состояние . Тепловой свет можно описать как статистическую смесь когерентных состояний, а типичный способ определения неклассического света состоит в том, что его нельзя описать как простую статистическую смесь когерентных состояний.

Собственные энергетические состояния линейного гармонического осциллятора (например, массы на пружинах, колебания решетки в твердом теле, колебательные движения ядер в молекулах или колебания в электромагнитном поле) представляют собой квантовые состояния с фиксированным числом. Состояние Фока (например, одиночный фотон) является наиболее похожим на частицу состоянием; он имеет фиксированное число частиц, а фаза неопределенна. Когерентное состояние распределяет свою квантово-механическую неопределенность поровну между канонически сопряженными координатами , положением и импульсом, а относительная неопределенность в фазе [определенная эвристически ] и амплитуде примерно равна — и мала при высокой амплитуде.

механическое

Математически когерентное состояние $|\alpha \rangle$ определяется как (единственное) собственное состояние оператора уничтожения â с соответствующим собственным значением α . Формально это звучит так:

${\hat {a}}|\alpha \rangle =\alpha |\alpha \rangle ~.$

Поскольку â не является эрмитовым , α , вообще говоря, является комплексным числом. Письмо $\alpha =|\alpha |e^{i\theta },$ | α | и θ называются амплитудой и фазой состояния. $|\alpha \rangle$.

Государство $|\alpha \rangle$ называется каноническим когерентным состоянием в литературе , поскольку существует множество других типов когерентных состояний, как можно увидеть в сопутствующей статье Когерентные состояния в математической физике .

Физически эта формула означает, что когерентное состояние остается неизменным при аннигиляции поля возбуждения или, скажем, частицы. Собственное состояние оператора уничтожения имеет распределение чисел Пуассона, если выражать его на основе собственных состояний энергии, как показано ниже. Распределение Пуассона является необходимым и достаточным условием того, что все обнаружения статистически независимы. Сравните это с одночастичным состоянием ( $|1\rangle$ Состояние Фока ): как только одна частица обнаружена, вероятность обнаружения другой равна нулю.

Для этого будут использоваться (нетрадиционно нормированные) безразмерные операторы X и P , обычно называемые квадратурами поля в квантовой оптике.(См. Обезразмеривание .) Эти операторы связаны с операторами положения и импульса массы m на пружине с постоянной k ,

${P}={\sqrt {\frac {1}{2\hbar m\omega }}}\ {\hat {p}}{\text{,}}\quad {X}={\sqrt {\frac {m\omega }{2\hbar }}}\ {\hat {x}}{\text{,}}\quad \quad {\text{where }}\omega \equiv {\sqrt {k/m}}~.$

Рисунок 4: Вероятность обнаружения n фотонов, распределение числа фотонов, когерентного состояния на рисунке 3. Поскольку это необходимо для пуассоновского распределения , среднее число фотонов равно дисперсии распределения числа фотонов. Столбцы относятся к теории, точки — к экспериментальным значениям.

Для поля оптического

$~E_{\rm {R}}=\left({\frac {2\hbar \omega }{\epsilon _{0}V}}\right)^{1/2}\!\!\!\cos(\theta )X\qquad {\text{and}}\qquad ~E_{\rm {I}}=\left({\frac {2\hbar \omega }{\epsilon _{0}V}}\right)^{1/2}\!\!\!\sin(\theta )X~$

– действительная и мнимая составляющие моды электрического поля внутри полости объёма $V$.

С этими (безразмерными) операторами гамильтониан любой системы принимает вид

${H}=\hbar \omega \left({P}^{2}+{X}^{2}\right){\text{,}}\qquad {\text{with}}\qquad \left[{X},{P}\right]\equiv {XP}-{PX}={\frac {i}{2}}\,{I}.$

Эрвин Шредингер искал состояния, наиболее близкие к классическим, когда впервые ввел гауссовы волновые пакеты с минимальной неопределенностью. Квантовое состояние гармонического осциллятора, которое минимизирует соотношение неопределенностей с неопределенностью, равномерно распределенной между X и P, удовлетворяет уравнению

$\left({X}-\langle {X}\rangle \right)\,|\alpha \rangle =-i\left({P}-\langle {P}\rangle \right)\,|\alpha \rangle {\text{,}}$

или, что то же самое,

$\left({X}+i{P}\right)\,\left|\alpha \right\rangle =\left\langle {X}+i{P}\right\rangle \,\left|\alpha \right\rangle ~,$

и, следовательно,

$\langle \alpha \!\mid \left({X}-\langle X\rangle \right)^{2}+\left({P}-\langle P\rangle \right)^{2}\mid \!\alpha \rangle =1/2~.$

Таким образом, учитывая (∆ X −∆ P ) ² ≥ 0 , Шрёдингер обнаружил, что минимальные состояния неопределенности для линейного гармонического осциллятора являются собственными состояниями ( X + iP ) . Поскольку â есть ( X + iP ) , это можно распознать как когерентное состояние в смысле приведенного выше определения.

Используя обозначения для многофотонных состояний, Глаубер охарактеризовал состояние полной когерентности всех порядков в электромагнитном поле как собственное состояние оператора уничтожения - формально, в математическом смысле, то же самое состояние, которое обнаружил Шредингер. Название «когерентное государство» появилось после работы Глаубера.

Если неопределенность сведена к минимуму, но не обязательно одинаково сбалансирована между X и P , состояние называется сжатым когерентным состоянием .

Положение когерентного состояния в комплексной плоскости ( фазовом пространстве ) сосредоточено в положении и импульсе классического осциллятора с фазой θ и амплитудой | α | задается собственным значением α (или тем же комплексным значением электрического поля для электромагнитной волны). Как показано на рисунке 5, неопределенность, равномерно распределенная во всех направлениях, представлена ​​диском диаметром 1 ⁄ 2 . При изменении фазы когерентное состояние вращается вокруг начала координат, а диск не искажается и не расширяется. Это наиболее похожее квантовое состояние на одну точку фазового пространства.

Рисунок 5: График фазового пространства когерентного состояния. Это показывает, что неопределенность в когерентном состоянии одинаково распределена во всех направлениях. Горизонтальная и вертикальная оси представляют собой квадратуры поля X и P соответственно (см. текст). Красные точки на оси X обозначают границы квантового шума на рисунке 1. Более подробно см. соответствующий рисунок формулировки фазового пространства .

Поскольку неопределенность (и, следовательно, шум измерения) остается постоянной при 1 ⁄ 2 по мере увеличения амплитуды колебаний, состояние ведет себя все больше как синусоидальная волна, как показано на рисунке 1. Более того, поскольку вакуумное состояние $|0\rangle$ Это всего лишь когерентное состояние с α = 0, все когерентные состояния имеют ту же неопределенность, что и вакуум. Следовательно, можно интерпретировать квантовый шум когерентного состояния как результат вакуумных флуктуаций.

Обозначения $|\alpha \rangle$ не относится к состоянию Фока . Например, при α = 1 не следует путать $|1\rangle$ для однофотонного фоковского состояния, которое также обозначают $|1\rangle$ в своих обозначениях. Выражение $|\alpha \rangle$ с α = 1 представляет собой распределение Пуассона числовых состояний $|n\rangle$ со средним числом фотонов, равным единице.

Формальным решением уравнения собственных значений является состояние вакуума, смещенное в положение α в фазовом пространстве, т.е. оно получается, позволяя оператору унитарного смещения D ( α ) действовать на вакуум:

$|\alpha \rangle =e^{\alpha {\hat {a}}^{\dagger }-\alpha ^{*}{\hat {a}}}|0\rangle =D(\alpha )|0\rangle$,

где â = X + iP и â ^† = Х - IP .

Это можно легко увидеть, как и практически все результаты, связанные с когерентными состояниями, используя представление когерентного состояния в базисе состояний Фока:

$|\alpha \rangle =e^{-{|\alpha |^{2} \over 2}}\sum _{n=0}^{\infty }{\alpha ^{n} \over {\sqrt {n!}}}|n\rangle =e^{-{|\alpha |^{2} \over 2}}e^{\alpha {\hat {a}}^{\dagger }}e^{-{\alpha ^{*}{\hat {a}}}}|0\rangle =e^{\alpha {\hat {a}}^{\dagger }-\alpha ^{*}{\hat {a}}}|0\rangle =D(\alpha )|0\rangle ~,$

где $|n\rangle$ — собственные векторы энергии (числа) гамильтониана

$H=\hbar \omega \left({\hat {a}}^{\dagger }{\hat {a}}+{\frac {1}{2}}\right)~,$

и окончательное равенство выводится из формулы Бейкера-Кэмпбелла-Хаусдорфа . Для соответствующего распределения Пуассона вероятность обнаружения n фотонов равна

$P(n)=|\langle n|\alpha \rangle |^{2}=e^{-\langle n\rangle }{\frac {\langle n\rangle ^{n}}{n!}}~.$

Аналогично, среднее число фотонов в когерентном состоянии равно

$~\langle n\rangle =\langle {\hat {a}}^{\dagger }{\hat {a}}\rangle =|\alpha |^{2}~$

и дисперсия

$~(\Delta n)^{2}={\rm {Var}}\left({\hat {a}}^{\dagger }{\hat {a}}\right)=|\alpha |^{2}~$.

То есть стандартное отклонение обнаруженного числа равно квадратному корню из обнаруженного числа. Таким образом, в пределе больших α эта статистика обнаружения эквивалентна статистике классической стабильной волны.

Эти результаты применимы к результатам обнаружения на одном детекторе и, таким образом, относятся к когерентности первого порядка (см. степень когерентности ). Однако для измерений, коррелирующих обнаружения на нескольких детекторах, используется когерентность более высокого порядка (например, корреляция интенсивности, когерентность второго порядка, на двух детекторах). Определение квантовой когерентности, данное Глаубером, включает в себя корреляционные функции n-го порядка (когерентность n-го порядка) для всех n . Идеальное когерентное состояние имеет все n-порядков корреляции, равных 1 (когерентное). Он идеально соответствует всем заказам.

Коэффициент корреляции второго порядка $g^{2}(0)$ дает прямую меру степени когерентности фотонных состояний с точки зрения дисперсии статистики фотонов в исследуемом пучке.

$~g^{2}(0)=1+{\frac {{\rm {Var}}\left({\hat {a}}^{\dagger }{\hat {a}}\right)-\langle {\hat {a}}^{\dagger }{\hat {a}}\rangle }{(\langle {\hat {a}}^{\dagger }{\hat {a}}\rangle )^{2}}}=1+{\frac {{\rm {Var}}(n)-{\bar {n}}}{{\bar {n}}^{2}}}$

В разработке Глаубера видно, что когерентные состояния распределяются согласно распределению Пуассона . В случае распределения Пуассона дисперсия равна среднему значению, т.е.

${\rm {Var}}(n)={\bar {n}}$

$g^{2}(0)=1$.

Коэффициент корреляции второго порядка, равный 1, означает, что фотоны в когерентных состояниях некоррелированы.

Хэнбери Браун и Твисс изучили корреляционное поведение фотонов, испускаемых тепловым некогерентным источником, описываемым статистикой Бозе-Эйнштейна . Дисперсия распределения Бозе – Эйнштейна равна

${\rm {Var(n)}}={\bar {n}}+{\bar {n}}^{2}$

$g^{2}(0)=2$.

Это соответствует корреляционным измерениям Хэнбери Брауна и Твисса и показывает, что фотоны в некогерентных состояниях Бозе-Эйнштейна коррелированы или сгруппированы.

Кванты, подчиняющиеся статистике Ферми – Дирака , антикоррелированы. В этом случае дисперсия

${\rm {Var}}(n)={\bar {n}}-{\bar {n}}^{2}$

$g^{2}(0)=0$.

Антикорреляция характеризуется коэффициентом корреляции второго порядка =0.

Работа Роя Дж. Глаубера была вызвана результатами Хэнбери-Брауна и Твисса, которые создали интерференционные картины первого порядка на большие расстояния (сотни или тысячи миль) за счет использования флуктуаций интенсивности (отсутствие когерентности второго порядка) с узкополосные фильтры (частичная когерентность первого порядка) на каждом детекторе. (Можно представить, что в течение очень коротких промежутков времени почти мгновенная интерференционная картина от двух детекторов из-за узкополосных фильтров, которая хаотично перемещается из-за смещения относительной разности фаз. При использовании счетчика совпадений танцующая интерференционная картина будет быть сильнее в моменты повышенной интенсивности (общего для обоих лучей), и эта картина будет сильнее, чем фоновый шум.) Почти вся оптика была связана с когерентностью первого порядка. Результаты Хэнбери-Брауна и Твисса побудили Глаубера взглянуть на когерентность более высокого порядка, и он пришел к полному квантово-теоретическому описанию когерентности всех порядков в электромагнитном поле (и квантово-теоретическому описанию сигнала и шума). . Он ввёл термин когерентное состояние и показал, что они образуются при взаимодействии классического электрического тока с электромагнитным полем.

При α ≫ 1 , как показано на рисунке 5, простая геометрия дает Δθ | α | = 1/2. Из этого следует, что существует компромисс между неопределенностью числа и неопределенностью фазы, Δθ Δn = 1/2, который иногда интерпретируется как соотношение неопределенности число-фаза; но это не формальное строгое соотношение неопределенностей: в квантовой механике не существует однозначно определенного фазового оператора.

Волновая функция когерентного состояния

Временная эволюция распределения вероятностей с квантовой фазой (цветом) когерентного состояния с α=3.

Чтобы найти волновую функцию когерентного состояния, волновой пакет Шрёдингера с минимальной неопределенностью, проще всего начать с гейзенберговской картины квантового гармонического осциллятора для когерентного состояния. $|\alpha \rangle$. Обратите внимание, что

$~a(t)|\alpha \rangle =e^{-i\omega t}a(0)|\alpha \rangle$

Когерентное состояние является собственным состоянием оператора уничтожения в картине Гейзенберга .

Легко видеть, что в картине Шрёдингера одно и то же собственное значение

$~\alpha (t)=e^{-i\omega t}\alpha (0)~$

происходит,

$~a|\alpha (t)\rangle =\alpha (t)|\alpha (t)\rangle$.

В координатных представлениях, возникающих в результате действия $\langle x|$, это составляет дифференциальное уравнение,

$~{\sqrt {\frac {m\omega }{2\hbar }}}\left(x+{\frac {\hbar }{m\omega }}{\frac {\partial }{\partial x}}\right)\psi ^{\alpha }(x,t)=\alpha (t)\psi ^{\alpha }(x,t)~,$

которое легко решается и дает

$~\psi ^{(\alpha )}(x,t)=\left({\frac {m\omega }{\pi \hbar }}\right)^{1/4}\exp {\Bigg (}-{\frac {m\omega }{2\hbar }}\left(x-{\sqrt {\frac {2\hbar }{m\omega }}}\Re [\alpha (t)]\right)^{2}+i{\sqrt {\frac {2m\omega }{\hbar }}}\Im [\alpha (t)]x+i\theta (t){\Bigg )}~,$

где θ(t) — еще неопределенная фаза, которую необходимо зафиксировать, потребовав, чтобы волновая функция удовлетворяла уравнению Шредингера.

Отсюда следует, что

$~\theta (t)=-{\frac {\omega t}{2}}+{\frac {|\alpha (0)|^{2}\sin(2\omega t-2\sigma )}{2}}~,{\text{where}}\qquad \alpha (0)\equiv |\alpha (0)|\exp(i\sigma )~,$

так что σ — начальная фаза собственного значения.

Среднее положение и импульс этого «минимального волнового пакета Шредингера» ψ ^(а) таким образом, колеблются так же, как классическая система ,

$\langle {\hat {x}}(t)\rangle ={\sqrt {\frac {2\hbar }{m\omega }}}\Re [\alpha (t)]=|\alpha (0)|{\sqrt {\frac {2\hbar }{m\omega }}}\cos(\sigma -\omega t)~,$

$\langle {\hat {p}}(t)\rangle ={\sqrt {2m\hbar \omega }}\Im [\alpha (t)]=|\alpha (0)|{\sqrt {2m\hbar \omega }}\sin(\sigma -\omega t)~.$

Плотность вероятности остается гауссовой с центром в этом колеблющемся среднем значении:

$|\psi ^{(\alpha )}(x,t)|^{2}={\sqrt {\frac {m\omega }{\pi \hbar }}}e^{-{\frac {m\omega }{\hbar }}\left(x-\langle {\hat {x}}(t)\rangle \right)^{2}}.$

канонических когерентных

Описанные до сих пор канонические когерентные состояния обладают тремя взаимно эквивалентными свойствами, поскольку каждое из них полностью определяет состояние. $|\alpha \rangle$, а именно,

1. Они являются собственными векторами оператора уничтожения : ${\hat {a}}|\alpha \rangle =\alpha |\alpha \rangle \,$.
2. Они получаются из вакуума применением унитарного оператора смещения : $|\alpha \rangle =e^{\alpha {\hat {a}}^{\dagger }-\alpha ^{*}{\hat {a}}}|0\rangle =D(\alpha )|0\rangle \,$.
3. Это состояния (сбалансированной) минимальной неопределенности: $\Delta X=\Delta P={\sqrt {\frac {\hbar }{2}}}\,$.

см. в статье « Когерентные состояния в математической физике Каждое из этих свойств может привести к обобщениям, в целом отличным друг от друга ( некоторые из них »). Мы подчеркиваем, что когерентные состояния имеют математические особенности, которые сильно отличаются от свойств состояния Фока ; например, два разных когерентных состояния не ортогональны,

$\langle \beta |\alpha \rangle =e^{-{1 \over 2}(|\beta |^{2}+|\alpha |^{2}-2\beta ^{*}\alpha )}\neq \delta (\alpha -\beta )$

(связано с тем, что они являются собственными векторами несамосопряженного оператора уничтожения â ).

Таким образом, если осциллятор находится в квантовом состоянии $|\alpha \rangle$ это также с ненулевой вероятностью и в другом квантовом состоянии $|\beta \rangle$ (но чем дальше друг от друга состояния расположены в фазовом пространстве, тем меньше вероятность). Однако, поскольку они подчиняются соотношению замыкания, любое состояние можно разложить на множество когерентных состояний. Следовательно, они образуют сверхполный базис , в котором можно диагонально разложить любое состояние. Это предпосылка P-представления Глаубера-Сударшана .

Это соотношение замыкания может быть выражено через разрешение тождественного оператора I в векторном пространстве квантовых состояний:

${\frac {1}{\pi }}\int |\alpha \rangle \langle \alpha |d^{2}\alpha =I\qquad d^{2}\alpha \equiv d\Re (\alpha )\,d\Im (\alpha )~.$

Это разрешение идентичности тесно связано с преобразованием Сигала – Баргмана .

Другая особенность состоит в том, что ${\hat {a}}^{\dagger }$ не имеет собственного числа (в то время как â не имеет собственного). Следующее равенство является ближайшим формальным заменителем и оказывается полезным для технических вычислений:

$a^{\dagger }|\alpha \rangle \langle \alpha |=\left({\partial \over \partial \alpha }+\alpha ^{*}\right)|\alpha \rangle \langle \alpha |~.$

Это последнее состояние известно как «состояние Агарвала» или когерентное состояние с добавлением фотонов и обозначается как $|\alpha ,1\rangle .$

Нормализованные состояния Агарвала порядка n можно выразить как $|\alpha ,n\rangle =[{{\hat {a}}^{\dagger }]}^{n}|\alpha \rangle /\|[{{\hat {a}}^{\dagger }]}^{n}|\alpha \rangle \|~.$

Вышеупомянутое разрешение идентичности может быть получено (ограничиваясь для простоты одним пространственным измерением), взяв матричные элементы между собственными состояниями положения, $\langle x|\cdots |y\rangle$, с обеих сторон уравнения. В правой части это сразу дает δ(xy) . В левой части то же самое получается вставкой

$\psi ^{\alpha }(x,t)=\langle x|\alpha (t)\rangle$

из предыдущего раздела (время произвольное), затем интегрируем по $\Im (\alpha )$ используя представление Фурье дельта-функции , а затем выполняя интеграл по Гауссу по $\Re (\alpha )$.

В частности, состояние гауссовского волнового пакета Шрёдингера следует из явного значения

$\langle x|\alpha \rangle ={\frac {1}{\pi ^{1/4}}}{e^{-{\frac {1}{2}}{(x-{\sqrt {2}}\Re (\alpha ))^{2}}+ix{\sqrt {2}}\Im (\alpha )-i\Re (\alpha )\Im (\alpha )}}~.$

Разрешение идентичности также может быть выражено через положение и импульс частицы. Для каждого координатного измерения (с использованием адаптированных обозначений с новым значением для $x$),

$|\alpha \rangle \equiv |x,p\rangle \qquad \qquad x\equiv \langle {\hat {x}}\rangle \qquad \qquad p\equiv \langle {\hat {p}}\rangle$

отношение замыкания когерентных состояний гласит:

$I=\int |x,p\rangle \,\langle x,p|~{\frac {\mathrm {d} x\,\mathrm {d} p}{2\pi \hbar }}~.$

Это можно вставить в любое квантовомеханическое математическое ожидание, связав его с некоторым квазиклассическим интегралом в фазовом пространстве и объяснив, в частности, происхождение нормировочных коэффициентов. $(2\pi \hbar )^{-1}$ для классических статистических сумм , соответствующих квантовым механика.

Когерентное состояние не только является точным собственным состоянием операторов уничтожения, но и является приблизительное общее собственное состояние положения и импульса частицы. Ограничение до снова одно измерение,

${\hat {x}}|x,p\rangle \approx x|x,p\rangle \qquad \qquad {\hat {p}}|x,p\rangle \approx p|x,p\rangle$

Ошибка в этих приближениях измеряется неопределенностями положения и импульса,

$\langle x,p|\left({\hat {x}}-x\right)^{2}|x,p\rangle =\left(\Delta x\right)^{2}\qquad \qquad \langle x,p|\left({\hat {p}}-p\right)^{2}|x,p\rangle =\left(\Delta p\right)^{2}~.$

Термическое

Одномодовое термическое когерентное состояние производится путем смещения термического смешанного состояния в фазовом пространстве по прямой аналогии смещению вакуумного состояния с целью генерации когерентного состояния. Матрица плотности когерентного теплового состояния в операторном представлении имеет вид

$\rho (\alpha ,\beta )={\frac {1}{Z}}D(\alpha )e^{-\hbar \beta \omega a^{\dagger }a}D^{\dagger }(\alpha ),$

где $D(\alpha )$ — оператор смещения , который генерирует когерентное состояние $D(\alpha )|0\rangle =|\alpha \rangle$ с комплексной амплитудой $\alpha$, и $\beta =1/(k_{B}T)$ . Функция распределения равна

$Z={\text{tr}}\left\{\displaystyle e^{-\hbar \beta \omega a^{\dagger }a}\right\}=\sum _{n=0}^{\infty }e^{-n\beta \hbar \omega }={\frac {1}{1-e^{-\hbar \beta \omega }}}.$

Используя разложение тождественного оператора в состояниях Фока , $I\equiv \sum _{n=0}^{\infty }|n\rangle \langle n|$, определение оператора плотности можно выразить в следующем виде

$\rho (\alpha ,\beta )={\frac {1}{Z}}\sum _{n=0}^{\infty }e^{-n\hbar \beta \omega }D(\alpha )|n\rangle \langle n|D^{\dagger }(\alpha )={\frac {1}{Z}}\sum _{n=0}^{\infty }e^{-n\hbar \beta \omega }|\alpha ,n\rangle \langle \alpha ,n|,$

где $|\alpha ,n\rangle$ означает смещенное государство Фока . Заметим, что если температура стремится к нулю, мы имеем

$\lim _{\beta \to \infty }\rho (\alpha ,\beta )=\lim _{\beta \to \infty }\sum _{n=0}^{\infty }e^{-n\hbar \beta \omega }(1-e^{-\hbar \beta \omega })|\alpha ,n\rangle \langle \alpha ,n|=\sum _{n=0}^{\infty }\delta _{n,0}|\alpha ,n\rangle \langle \alpha ,n|=|\alpha ,0\rangle \langle \alpha ,0|,$

что является матрицей плотности когерентного состояния. Среднее количество фотонов в этом состоянии можно рассчитать, как показано ниже.

$\langle n\rangle ={\text{Tr}}\{\rho a^{\dagger }a\}={\frac {1}{Z}}{\text{Tr}}\{D^{\dagger }(\alpha )a^{\dagger }D({\alpha })D^{\dagger }(\alpha )aD(\alpha )e^{-\beta \hbar \omega a^{\dagger }a}\}={\frac {1}{Z}}{\text{Tr}}\{(a^{\dagger }+\alpha ^{*})(a+\alpha )e^{-\beta \hbar \omega a^{\dagger }a}\}=$

$=|\alpha |^{2}{\frac {1}{Z}}{\text{Tr}}\{e^{-\beta \hbar \omega a^{\dagger }a}\}+{\frac {1}{Z}}{\text{Tr}}\{a^{\dagger }ae^{-\beta \hbar \omega a^{\dagger }a}\}=|\alpha |^{2}+{\frac {1}{Z}}\sum _{n=0}^{\infty }ne^{-n\beta \hbar \omega },$

где для последнего члена мы можем написать

$\sum _{n=0}^{\infty }ne^{-n\beta \hbar \omega }=-{\frac {\partial }{\partial (\beta \hbar \omega )}}\left(\sum _{n=0}^{\infty }e^{-n\beta \hbar \omega }\right)={\frac {e^{-\beta \hbar \omega }}{(1-e^{-\beta \hbar \omega })^{2}}}.$

В результате мы находим

$\langle n\rangle =|\alpha |^{2}+\langle n\rangle _{\text{th}},$

где $\langle n\rangle _{\text{th}}$ представляет собой среднее число фотонов , рассчитанное с учетом теплового состояния. Здесь мы определили для простоты обозначений

$\langle O\rangle _{\text{th}}={\frac {1}{Z}}{\text{tr}}\{e^{-\beta \hbar \omega a^{\dagger }a}O\},$

и мы пишем явно

$\langle n\rangle _{\text{th}}={\frac {1}{e^{\beta \hbar \omega }-1}}.$

В пределе $\beta \to \infty$ мы получаем $\langle n\rangle =|\alpha |^{2}$, что согласуется с выражением для оператора матрицы плотности при нулевой температуре. числа фотонов Аналогично, дисперсию можно оценить как

$\sigma ^{2}=\langle n^{2}\rangle -\langle n\rangle ^{2}=\sigma _{\text{th}}^{2}+|\alpha |^{2}\left(1+2\langle a^{\dagger }a\rangle _{\text{th}}\right),$

с $\sigma _{\text{th}}^{2}=\langle n^{2}\rangle _{\text{th}}-\langle n\rangle _{\text{th}}^{2}$. Делаем вывод, что второй момент не может быть отделен от теплового и квантового моментов распределения, в отличие от среднего значения (первого момента). В этом смысле статистика фотонов смещенного теплового состояния не описывается суммой статистики Пуассона и статистики Больцмана . Распределение начального теплового состояния в фазовом пространстве расширяется в результате когерентного смещения.

конденсатов Бозе –

• ( Конденсат Бозе-Эйнштейна БЭК) представляет собой совокупность атомов бозонов, находящихся в одном квантовом состоянии. В термодинамической системе основное состояние становится макроскопически занятым ниже критической температуры — примерно тогда, когда тепловая длина волны де Бройля превышает межатомное расстояние. Считается, что сверхтекучесть жидкого гелия-4 связана с бозе-эйнштейновской конденсацией в идеальном газе. Но ⁴ Он обладает сильными взаимодействиями, и важную роль играет структурный фактор жидкости (статистика 2-го порядка). Использование когерентного состояния для представления сверхтекучего компонента ⁴ Он дал хорошую оценку фракций конденсата/неконденсата в сверхтекучести, согласующуюся с результатами рассеяния медленных нейтронов. Большинство особых свойств сверхтекучести напрямую вытекают из использования когерентного состояния для представления сверхтекучего компонента, который действует как макроскопически занятое состояние одного тела с четко определенной амплитудой и фазой по всему объему. (Сверхтекучий компонент ⁴ Он идет от нуля при температуре перехода до 100% при абсолютном нуле. Но доля конденсата около 6%. при абсолютной нулевой температуре Т=0К.)
• В начале изучения сверхтекучести Пенроуз и Онзагер предложили метрику («параметр порядка») для сверхтекучести. Он был представлен макроскопической факторизованной составляющей (макроскопическим собственным значением) в приведенной матрице плотности первого порядка. Позже CN Ян предложил более обобщенную меру макроскопической квантовой когерентности, названную «Недиагональный дальний порядок» (ODLRO), это включало как фермионные, так и бозонные системы. ODLRO существует всякий раз, когда в приведенной матрице плотности любого порядка имеется макроскопически большой факторизованный компонент (собственное значение). Сверхтекучесть соответствует большому факторизованному компоненту в приведенной матрице плотности первого порядка. (И все матрицы приведенной плотности более высокого порядка ведут себя аналогичным образом.) Сверхпроводимость включает в себя большой факторизованный компонент в приведенной матрице плотности 2-го порядка (« Куперовская электронная пара »).
• Приведенные матрицы плотности, используемые для описания макроскопической квантовой когерентности в сверхтекучих средах, формально совпадают с корреляционными функциями, используемыми для описания порядков когерентности в излучении. Оба являются примерами макроскопической квантовой когерентности. Макроскопически большой когерентный компонент плюс шум в электромагнитном поле, как указано в описании Глаубера сигнала плюс шум, формально аналогичен макроскопически большому сверхтекучему компоненту плюс нормальный жидкостный компонент в двухжидкостной модели сверхтекучести.
• Повседневное электромагнитное излучение, такое как радио- и телевизионные волны, также является примером почти когерентных состояний (макроскопической квантовой когерентности). Это должно «заставить задуматься» относительно традиционного разграничения между квантовым и классическим.
• Когерентность в сверхтекучести не следует приписывать какому-либо подмножеству атомов гелия; это своего рода коллективное явление, в котором участвуют все атомы (аналогично куперовскому спариванию в сверхпроводимости, как указано в следующем разделе).

Когерентные электронные состояния в сверхпроводимости

• Электроны — это фермионы, но когда они объединяются в куперовские пары, они действуют как бозоны и поэтому могут вместе образовывать когерентное состояние при низких температурах. На самом деле это спаривание происходит не между электронами, а в состояниях, доступных электронам, входящим и выходящим из этих состояний. Куперовское спаривание относится к первой модели сверхпроводимости.
• Эти когерентные состояния являются частью объяснения таких эффектов, как квантовый эффект Холла в низкотемпературных сверхпроводящих полупроводниках.

Обобщения

• По мнению Гилмора и Переломова, которые показали это независимо, построение когерентных состояний можно рассматривать как проблему в теории групп , и, таким образом, когерентные состояния могут быть связаны с группами, отличными от группы Гейзенберга , что приводит к каноническим когерентным состояниям, обсуждавшимся выше. . Более того, эти когерентные состояния могут быть обобщены на квантовые группы . Эти темы со ссылками на оригинальные работы подробно обсуждаются в книге «Когерентные состояния в математической физике» .

• В квантовой теории поля и теории струн — обобщение когерентных состояний на случай, когда бесконечное число степеней свободы используется для определения вакуумного состояния с вакуумным математическим ожиданием, отличным от исходного вакуума.
• В одномерных квантовых системах многих тел с фермионными степенями свободы возбужденные состояния с низкой энергией можно аппроксимировать как когерентные состояния оператора бозонного поля, который создает возбуждения частица-дырка. Этот подход называется бозонизацией .
• Гауссовы когерентные состояния нерелятивистской квантовой механики можно обобщить до релятивистских когерентных состояний частиц Клейна-Гордона и Дирака.
• Когерентные состояния также появлялись в работах по петлевой квантовой гравитации или при построении (полу)классической канонической квантовой общей теории относительности.

См. также

• Когерентные состояния в математической физике
• Квантовая теория поля
• Квантовая оптика
• Квантовый усилитель
• Электромагнитное поле
• Степень согласованности

Внешние ссылки

• Квантовые состояния светового поля
• Глауберовые состояния: когерентные состояния квантового гармонического осциллятора.
• Измерьте когерентное состояние с помощью интерактивной статистики фотонов