расстройство

О психологическом состоянии см. психоз .

Число возможных перестановок и перестановок n элементов. н ! ( n факториал) — количество n -перестановок; ! n ( n субфакториал) — количество нарушений — n -перестановок, при которых все n элементов меняют свои исходные места.

showТаблица значений
$n$	Permutations, $n!$	Derangements, $!n$	${\frac {!n}{n!}}$
0	1 =1×100	1 =1×100	= 1
1	1 =1×100	0	= 0
2	2 =2×100	1 =1×100	= 0.5
3	6 =6×100	2 =2×100	≈0.33333 33333
4	24 =2.4×101	9 =9×100	= 0.375
5	120 =1.20×102	44 =4.4×101	≈0.36666 66667
6	720 =7.20×102	265 =2.65×102	≈0.36805 55556
7	5,040 =5.04×103	1,854 ≈1.85×103	≈0.36785,71429
8	40,320 ≈4.03×104	14,833 ≈1.48×104	≈0.36788 19444
9	362,880 ≈3.63×105	133,496 ≈1.33×105	≈0.36787 91887
10	3,628,800 ≈3.63×106	1,334,961 ≈1.33×106	≈0.36787 94643
11	39,916,800 ≈3.99×107	14,684,570 ≈1.47×107	≈0.36787 94392
12	479,001,600 ≈4.79×108	176,214,841 ≈1.76×108	≈0.36787 94413
13	6,227,020,800 ≈6.23×109	2,290,792,932 ≈2.29×109	≈0.36787 94412
14	87,178,291,200 ≈8.72×1010	32,071,101,049 ≈3.21×1010	≈0.36787 94412
15	1,307,674,368,000 ≈1.31×1012	481,066,515,734 ≈4.81×1011	≈0.36787 94412
16	20,922,789,888,000 ≈2.09×1013	7,697,064,251,745 ≈7.70×1012	≈0.36787 94412
17	355,687,428,096,000 ≈3.56×1014	130,850,092,279,664 ≈1.31×1014	≈0.36787 94412
18	6,402,373,705,728,000 ≈6.40×1015	2,355,301,661,033,953 ≈2.36×1015	≈0.36787 94412
19	121,645,100,408,832,000 ≈1.22×1017	44,750,731,559,645,106 ≈4.48×1016	≈0.36787 94412
20	2,432,902,008,176,640,000 ≈2.43×1018	895,014,631,192,902,121 ≈8.95×1017	≈0.36787 94412
21	51,090,942,171,709,440,000 ≈5.11×1019	18,795,307,255,050,944,540 ≈1.88×1019	≈0.36787 94412
22	1,124,000,727,777,607,680,000 ≈1.12×1021	413,496,759,611,120,779,881 ≈4.13×1020	≈0.36787 94412
23	25,852,016,738,884,976,640,000 ≈2.59×1022	9,510,425,471,055,777,937,262 ≈9.51×1021	≈0.36787 94412
24	620,448,401,733,239,439,360,000 ≈6.20×1023	228,250,211,305,338,670,494,289 ≈2.28×1023	≈0.36787 94412
25	15,511,210,043,330,985,984,000,000 ≈1.55×1025	5,706,255,282,633,466,762,357,224 ≈5.71×1024	≈0.36787 94412
26	403,291,461,126,605,635,584,000,000 ≈4.03×1026	148,362,637,348,470,135,821,287,825 ≈1.48×1026	≈0.36787 94412
27	10,888,869,450,418,352,160,768,000,000 ≈1.09×1028	4,005,791,208,408,693,667,174,771,274 ≈4.01×1027	≈0.36787 94412
28	304,888,344,611,713,860,501,504,000,000 ≈3.05×1029	112,162,153,835,443,422,680,893,595,673 ≈1.12×1029	≈0.36787 94412
29	8,841,761,993,739,701,954,543,616,000,000 ≈8.84×1030	3,252,702,461,227,859,257,745,914,274,516 ≈3.25×1030	≈0.36787 94412
30	265,252,859,812,191,058,636,308,480,000,000 ≈2.65×1032	97,581,073,836,835,777,732,377,428,235,481 ≈9.76×1031	≈0.36787 94412

В комбинаторной математике расстройство — это перестановка элементов множества , при которой ни один элемент не появляется в исходном положении. Другими словами, расстройство — это перестановка, не имеющая фиксированных точек .

Число нарушений набора размера n известно как субфакториал числа n , или n- го числа нарушений , или n- го числа де Монмора (в честь Пьера Ремона де Монмора ). Обычно используемые обозначения субфакториалов включают ! n, D _n , d _n или n ¡.

При n > 0 субфакториал ! n равно ближайшему к n !/ e целому числу, где n ! обозначает факториал n , а e — число Эйлера .

Проблема подсчета расстройств была впервые рассмотрена Пьером Раймоном де Монмором в его «Эссе анализа сюр ле игры опасности» . в 1708 г.; он решил ее в 1713 году, как и Николай Бернулли примерно в то же время.

Пример

Выделены 9 нарушений (из 24 перестановок).

Предположим, что профессор дал тест 4 студентам — A, B, C и D — и хочет, чтобы они оценивали тесты друг друга. Конечно, ни один студент не должен оценивать свой собственный тест. Сколькими способами профессор мог вернуть тесты студентам для выставления оценок так, чтобы ни один студент не получил обратно свой тест? Из 24 возможных вариантов (4!) сдачи тестов,

АВСД ,	АБ ДК,	А КБ Д ,	ЦКБ ,	ДБК ,	А Д С Б,
БА компакт-диск ,	БАДК ,	БСА Д ,	БЦДА ,	БДАК ,	БД С А,
КАБИНА Д ,	КАБР ,	С Б А Д ,	С Б ДА,	ЦДАБ ,	ЦДБА ,
ДАБК ,	ДА С Б,	Д Б А С,	Д БК А,	ДКАБ ,	ДКБА .

всего 9 нарушений (показаны синим курсивом выше). В каждой другой перестановке этого набора из 4 человек по крайней мере один учащийся получает обратно свой тест (выделен жирным красным).

Другой вариант проблемы возникает, когда мы задаем вопрос о том, сколько способов можно поместить n писем, каждое из которых адресовано разным лицам, в n конвертов с заранее адресованным адресом, так что ни одно письмо не окажется в конверте с правильным адресом.

Подсчет нарушений

Подсчет нарушений набора сводится к задаче проверки шляп , в которой рассматривается количество способов, которыми шляп (назовем их h1 _от до hn ₎ можно вернуть n людям ( от _P1 до Pn _n ) таким образом, что ни шляпа возвращается к своему владельцу.

Каждый человек может получить любую из n − 1 шляп, не принадлежащую ему. Назовите шляпу, которую человек P _1, получает и _hi считайте владельцем _: ее P i _{получает} либо P ₁ шляпу , h ₁ , либо какую-то другую. Соответственно, проблема распадается на два возможных случая:

1. P _i получает шляпу, отличную от h ₁ . Этот случай эквивалентен решению задачи с n − 1 человеком и n − 1 шапками, поскольку для каждого из n − 1 человека, кроме P _1, − 1 шапок есть ровно одна шапка среди оставшихся n , которую они могут не получить (при любого Pj _для , кроме Pi _, неприемлемой шляпой является hj _, а Pi _для — h1 _. ) переименовать h ₁ в hi _{Другой способ убедиться в этом —} , где неисправность более очевидна: для любого от 2 до n j P _j не может получить h _j .
2. P _i получает h ₁ . В этом случае проблема сводится к n - 2 людям и n - 2 шляпам, потому что P ₁ получил h _i шляпу , а P _i получил h _{1 , что фактически исключает обоих из дальнейшего рассмотрения.} шляпу

Для каждой из n − 1 шляп, которые может получить P ₁ , количество способов, которыми P ₂ , ..., P _n могут получить шляпы, представляет собой сумму подсчетов для двух случаев.

Это дает нам решение проблемы проверки шляпы: алгебраически говоря, число ! n нарушений набора из n -элементов равно

$!n=(n-1)\cdot ({!(n-1)}+{!(n-2)})$ для $n\geq 2$,

где $!0=1$ и $!1=0$.

Количество нарушений малой длины приведено в таблице ниже.

Число нарушений n -элементного набора (последовательность A000166 в OEIS ) для малых n

н	0	1	2	3	4	5	6	7	8	9	10	11	12	13
! н	1	0	1	2	9	44	265	1,854	14,833	133,496	1,334,961	14,684,570	176,214,841	2,290,792,932

Существуют и другие выражения для ! n , что эквивалентно приведенной выше формуле. К ним относятся

$!n=n!\sum _{i=0}^{n}{\frac {(-1)^{i}}{i!}}$ для $n\geq 0$

и

$!n=\left[{\frac {n!}{e}}\right]=\left\lfloor {\frac {n!}{e}}+{\frac {1}{2}}\right\rfloor$ для $n\geq 1,$

где $\left[x\right]$ — ближайшая целочисленная функция и $\left\lfloor x\right\rfloor$ это функция пола .

Другие связанные формулы включают в себя

$$!n=\left\lfloor {\frac {n!+1}{e}}\right\rfloor ,\quad \ n\geq 1,$$

$$!n=\left\lfloor \left(e+e^{-1}\right)n!\right\rfloor -\lfloor en!\rfloor ,\quad n\geq 2,$$

и

$$!n=n!-\sum _{i=1}^{n}{n \choose i}\cdot {!(n-i)},\quad \ n\geq 1.$$

Также имеет место следующее повторение:

$$!n={\begin{cases}1&{\text{if }}n=0,\\n\cdot \left(!(n-1)\right)+(-1)^{n}&{\text{if }}n>0.\end{cases}}$$

Вывод по принципу включения-исключения

вывести нерекурсивную формулу для числа нарушений n Можно также -множества. Для $1\leq k\leq n$ мы определяем $S_{k}$ быть набором перестановок n объектов, которые фиксируют $k$-й объект. Любое пересечение набора из i этих множеств фиксирует конкретный набор из i объектов и, следовательно, содержит $(n-i)!$ перестановки. Есть ${\textstyle {n \choose i}}$ такие коллекции, поэтому принцип включения-исключения дает

$${\begin{aligned}|S_{1}\cup \dotsm \cup S_{n}|&=\sum _{i}\left|S_{i}\right|-\sum _{i<j}\left|S_{i}\cap S_{j}\right|+\sum _{i<j<k}\left|S_{i}\cap S_{j}\cap S_{k}\right|+\cdots +(-1)^{n+1}\left|S_{1}\cap \dotsm \cap S_{n}\right|\\&={n \choose 1}(n-1)!-{n \choose 2}(n-2)!+{n \choose 3}(n-3)!-\cdots +(-1)^{n+1}{n \choose n}0!\\&=\sum _{i=1}^{n}(-1)^{i+1}{n \choose i}(n-i)!\\&=n!\ \sum _{i=1}^{n}{(-1)^{i+1} \over i!},\end{aligned}}$$

и поскольку расстройство — это перестановка, которая не оставляет неподвижным ни один из n объектов, это подразумевает

$$!n=n!-\left|S_{1}\cup \dotsm \cup S_{n}\right|=n!\sum _{i=0}^{n}{\frac {(-1)^{i}}{i!}}.$$

С другой стороны, $n!=\sum _{i=0}^{n}{\binom {n}{i}}!i$ поскольку мы можем выбрать n - i элементов, которые будут находиться на своем месте, ивывести из строя другие элементы i только !i способами, по определению.

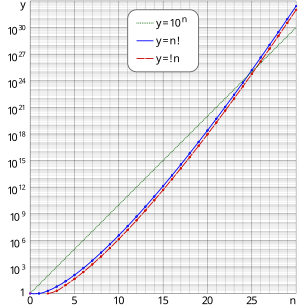
Рост количества нарушений по мере приближения n к ∞

От

$$!n=n!\sum _{i=0}^{n}{\frac {(-1)^{i}}{i!}}$$

и

$$e^{x}=\sum _{i=0}^{\infty }{x^{i} \over i!}$$

заменив $\textstyle x=-1$ сразу получается, что

$$\lim _{n\to \infty }{!n \over n!}=\lim _{n\to \infty }\sum _{i=0}^{n}{\frac {(-1)^{i}}{i!}}=e^{-1}\approx 0.367879\ldots .$$

Это предел вероятности того , что случайно выбранная перестановка большого количества объектов является расстройством. Вероятность очень быстро сходится к этому пределу с увеличением n , вот почему ! n — ближайшее целое число к n !/ e . Приведенный выше полулогарифмический график показывает, что график нарушений отстает от графа перестановок почти на постоянное значение.

Более подробную информацию об этом расчете и вышеуказанном лимите можно найти в статье о статистика случайных перестановок .

по числам

Асимптотическое разложение числа нарушений через числа Белла выглядит следующим образом:

$$!n={\frac {n!}{e}}+\sum _{k=1}^{m}\left(-1\right)^{n+k-1}{\frac {B_{k}}{n^{k}}}+O\left({\frac {1}{n^{m+1}}}\right),$$

где $m$ любое фиксированное положительное целое число, и $B_{k}$ обозначает $k$-й номер звонка . Более того, константа, подразумеваемая большим О -членом, не превосходит $B_{m+1}$.

Обобщения

Проблема встреч спрашивает, сколько перестановок множества размера n имеют ровно k неподвижных точек.

Нарушения являются примером более широкой области ограниченных перестановок. Например, задача о мужчине спрашивает: если n пар противоположного пола сидят мужчина-женщина-мужчина-женщина... за столом, сколькими способами они могут рассадиться так, чтобы никто не сидел рядом со своим партнером?

Более формально, учитывая множества A и S и некоторые наборы U и V сюръекций A S → , мы часто хотим знать количество пар функций ( f , g ) таких, что f находится в U , а g находится в V , и для всех a в A ; f ( a ) ≠ g ( a ) другими словами, где для каждых f и g существует нарушение φ группы S такое, что f ( a ) = φ( g ( a )).

Другим обобщением является следующая проблема:

Сколько существует анаграмм, в которых нет фиксированных букв данного слова?

Например, для слова, состоящего всего из двух разных букв, скажем, n букв A и m букв B, ответ, конечно, будет 1 или 0 в зависимости от того, n = m или нет, поскольку это единственный способ образовать анаграмму без фиксированных букв — это замена всех A на B , что возможно тогда и только тогда, когда n = m . В общем случае для слова, состоящего из n ₁ букв X ₁ , n ₂ букв X ₂ , ..., n _r букв X _r , оказывается (после правильного использования формулы включения-исключения ), что ответ имеет форма

$$\int _{0}^{\infty }P_{n_{1}}(x)P_{n_{2}}(x)\cdots P_{n_{r}}(x)e^{-x}\,dx,$$

некоторой последовательности полиномов Pn _для , где Pn _n имеет степень . Но приведенный выше ответ для случая r = 2 дает отношение ортогональности, следовательно, P _n являются полиномами Лагерра ( с точностью до знака, который легко определить).

$\int _{0}^{\infty }(t-1)^{z}e^{-t}dt$ в сложной плоскости

В частности, для классических расстройств имеет место следующее:

$$!n={\frac {\Gamma (n+1,-1)}{e}}=\int _{0}^{\infty }(x-1)^{n}e^{-x}dx$$

где $\Gamma (s,x)$ – верхняя неполная гамма-функция .

сложность

NP -полно определить, содержит ли данная группа перестановок (описываемая заданным набором перестановок, которые ее порождают) какие-либо нарушения.

Внешние ссылки

• Баэз, Джон (2003). «Давайте сходить с ума!» (PDF) .
• Богарт, Кеннет П.; Дойл, Питер Г. (1985). «Несексистское решение проблемы хозяйства» .
• Вайсштейн, Эрик В. «Расстройство» . MathWorld – веб-ресурс Wolfram.