Класс эквивалентности

В математике , когда элементы некоторого множества есть понятие эквивалентности (формализованное как отношение эквивалентности ), то можно естественным образом разбить множество на классы эквивалентности . Эти классы эквивалентности построены так, что элементы и принадлежат одному и тому же классу эквивалентности тогда и только тогда , когда они эквивалентны.
Формально, учитывая набор и отношение эквивалентности на класс эквивалентности элемента в обозначается или, что то же самое, подчеркнуть его отношение эквивалентности Определение отношений эквивалентности подразумевает, что классы эквивалентности разбиение образуют это означает, что каждый элемент множества принадлежит ровно одному классу эквивалентности.Множество классов эквивалентности иногда фактормножеством или факторпространством называют к и обозначается
Когда набор имеет некоторую структуру (например, групповую операцию или топологию ) и отношение эквивалентности совместим с этой структурой, фактормножество часто наследует аналогичную структуру от своего родительского набора. Примеры включают фактор-пространства в линейной алгебре , фактор-пространства в топологии , фактор-группы , однородные пространства , фактор-кольца , фактор-моноиды и фактор-категории .
Определение и обозначения [ править ]
Отношение эквивалентности на множестве это бинарное отношение на удовлетворяющий трем свойствам: [1]
- для всех ( рефлексивность ),
- подразумевает для всех ( симметрия ),
- если и затем для всех ( транзитивность ).
Класс эквивалентности элемента определяется как [2]
Слово «класс» в термине «класс эквивалентности» обычно можно рассматривать как синоним слова « множество », хотя некоторые классы эквивалентности являются не множествами, а собственными классами . Например, «быть изоморфным » — это отношение эквивалентности на группах , а классы эквивалентности, называемые классами изоморфизма , не являются множествами.
Множество всех классов эквивалентности в относительно отношения эквивалентности обозначается как и называется модуль (или факторный набор к ). [3] Сюръективная карта от на который отображает каждый элемент в его класс эквивалентности, называется каноническая сюръекция или каноническая проекция .
Каждый элемент класса эквивалентности характеризует этот класс и может использоваться для его представления . Когда такой элемент выбран, его называют представителем класса. Выбор представителя в каждом классе определяет инъекцию из до Х. Поскольку его композиция с канонической сюръекцией есть тождество такая инъекция называется секцией , если использовать терминологию теории категорий .
Иногда есть раздел, который более «естественен», чем другие. В этом случае представители называются каноническими представителями . Например, в модульной арифметике для каждого целого числа m, большего 1 , сравнение по модулю m является отношением эквивалентности целых чисел, для которого два целых числа a и b эквивалентны (в этом случае говорят, что конгруэнтны ), если m делит это обозначается Каждый класс содержит уникальное неотрицательное целое число, меньшее и эти целые числа являются каноническими представителями.
Использование представителей для представления классов позволяет избежать явного рассмотрения классов как множеств. В этом случае каноническая сюръекция, сопоставляющая элемент с его классом, заменяется функцией, сопоставляющей элемент с представителем его класса. В предыдущем примере эта функция обозначена и производит остаток деления на a m евклидова .
Свойства [ править ]
Каждый элемент из является членом класса эквивалентности Каждые два класса эквивалентности и либо равны, либо не пересекаются . Следовательно, множество всех классов эквивалентности образует перегородку : каждый элемент принадлежит одному и только одному классу эквивалентности. [4] И наоборот, каждое разделение возникает из отношения эквивалентности таким образом, согласно которому тогда и только тогда, когда и принадлежат одному набору раздела. [5]
Из свойств предыдущего раздела следует, что если является отношением эквивалентности на множестве и и два элемента следующие утверждения эквивалентны:
Примеры [ править ]
- Позволять быть множеством всех прямоугольников на плоскости, и отношение эквивалентности «имеет ту же площадь, что и», то для каждого положительного действительного числа будет класс эквивалентности всех прямоугольников, площадь которых [6]
- Рассмотрим отношение эквивалентности по модулю 2 на множестве целых чисел , такой, что тогда и только тогда, когда их разница это четное число . Это отношение порождает ровно два класса эквивалентности: один класс состоит из всех четных чисел, а другой класс состоит из всех нечетных чисел. Использование квадратных скобок вокруг одного члена класса для обозначения класса эквивалентности в этом отношении: и все представляют один и тот же элемент [2]
- Позволять быть набором упорядоченных пар целых чисел с ненулевым и определим отношение эквивалентности на такой, что тогда и только тогда, когда то класс эквивалентности пары можно отождествить с рациональным числом и это отношение эквивалентности и его классы эквивалентности можно использовать для формального определения множества рациональных чисел. [7] Эту же конструкцию можно обобщить на поле частных любой области целостности .
- Если состоит из всех прямых, скажем, в евклидовой плоскости , и означает, что и являются параллельными линиями , то набор прямых, параллельных друг другу, образует класс эквивалентности, пока линия считается параллельной самой себе . В этой ситуации каждый класс эквивалентности определяет точку на бесконечности .
Графическое представление [ править ]
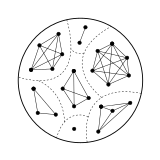
может Неориентированный граф быть связан с любым симметричным отношением на множестве. где вершины являются элементами и две вершины и соединены тогда и только тогда, когда К числу таких графов относятся графы отношений эквивалентности. Эти графы, называемые кластерными графами которых , характеризуются как графы, компоненты связности являются кликами . [2]
Инварианты [ править ]
Если является отношением эквивалентности на и является свойством элементов такое, что всякий раз, когда верно, если верно, то свойство называется инвариантом или четко определен в соответствии с соотношением
Частый частный случай имеет место, когда это функция от в другой набор ; если в любое время затем называется инвариантом класса относительно или просто инвариант относительно Это происходит, например, в теории характеров конечных групп. Некоторые авторы используют «совместимый с " или просто "уважает " вместо "инвариант при ".
Любая функция является классовым инвариантом относительно согласно которому тогда и только тогда, когда Класс эквивалентности представляет собой совокупность всех элементов которые сопоставляются с то есть класс является обратным образом отношение эквивалентности называется ядром Это
В более общем смысле, функция может отображать эквивалентные аргументы (в соответствии с отношением эквивалентности на ) к эквивалентным значениям (при отношении эквивалентности на ). Такая функция является морфизмом множеств, наделенным отношением эквивалентности.
Факторпространство в топологии [ править ]
В топологии факторпространство сформированное — это топологическое пространство, на множестве классов эквивалентности отношения эквивалентности в топологическом пространстве с использованием топологии исходного пространства для создания топологии на множестве классов эквивалентности.
В абстрактной алгебре отношения сравнения на базовом множестве алгебры позволяют алгебре индуцировать алгебру на классах эквивалентности отношения, называемую факторалгеброй . В линейной алгебре фактор -пространство — это векторное пространство, образованное фактор-группой , где фактор-гомоморфизм является линейным отображением . В более широком смысле, в абстрактной алгебре термин фактор-пространство может использоваться для фактор-модулей , фактор-колец , фактор-групп или любой фактор-алгебры. Однако использование этого термина для более общих случаев часто можно проводить по аналогии с орбитами действия группы.
Орбиты действия группы на множестве можно назвать фактор-пространством действия на множестве, особенно когда орбиты действия группы являются правыми смежными классами подгруппы группы, которые возникают в результате действия подгруппы на множестве. группа по левым сдвигам или, соответственно, левые смежные классы как орбиты при правом сдвиге.
Нормальная подгруппа топологической группы, действующая на группу действием трансляции, представляет собой факторпространство в смысле топологии, абстрактной алгебры и групповых действий одновременно.
Хотя этот термин можно использовать для обозначения любого набора классов эквивалентности в отношении эквивалентности, возможно, с дополнительной структурой, цель использования этого термина обычно состоит в том, чтобы сравнить этот тип отношения эквивалентности на множестве. либо к отношению эквивалентности, которое индуцирует некоторую структуру на множестве классов эквивалентности, из структуры того же типа на или к орбитам группового действия. Как смысл структуры, сохраняемой отношением эквивалентности, так и изучение инвариантов относительно действий группы приводят к приведенному выше определению инвариантов отношений эквивалентности.
См. также [ править ]
- Разделение эквивалентности — метод разработки наборов тестов при тестировании программного обеспечения , основанный на разделении возможных входных данных программы на классы эквивалентности в соответствии с поведением программы на этих входных данных.
- Однородное пространство , фактор-пространство групп Ли
- Отношение частичной эквивалентности - математическая концепция сравнения объектов.
- Фактор по отношению эквивалентности - Обобщение классов эквивалентности в теорию схем
- Сетоид - математическое построение множества с отношением эквивалентности.
- Трансверсаль (комбинаторика) - множество, пересекающее каждое из семейства множеств.
Примечания [ править ]
- ^ Девлин 2004 , с. 122.
- ↑ Перейти обратно: Перейти обратно: а б с Девлин 2004 , с. 123.
- ^ Вольф 1998 , с. 178
- ^ Мэддокс 2002 , с. 74, эт. 2.5.15
- ^ Авельсгаард 1989 , с. 132, Тм. 3.16
- ^ Авельсгаард 1989 , с. 127
- ^ Мэддокс 2002 , стр. 77–78.
Ссылки [ править ]
- Авелсгаард, Кэрол (1989), Основы высшей математики , Скотт Форесман, ISBN 0-673-38152-8
- Девлин, Кейт (2004), Множества, функции и логика: введение в абстрактную математику (3-е изд.), Chapman & Hall/CRC Press, ISBN 978-1-58488-449-1
- Мэддокс, Рэндалл Б. (2002), Математическое мышление и письмо , Harcourt/ Academic Press, ISBN 0-12-464976-9
- Вольф, Роберт С. (1998), Доказательство, логика и гипотеза: набор инструментов математика , Фриман, ISBN 978-0-7167-3050-7
Дальнейшее чтение [ править ]
- Сундстрем (2003), Математическое рассуждение: написание и доказательство , Прентис-Холл
- Смит; Эгген; Сент-Андре (2006), Переход к высшей математике (6-е изд.), Томсон (Брукс/Коул)
- Шумахер, Кэрол (1996), Глава нулевая: Фундаментальные понятия абстрактной математики , Аддисон-Уэсли, ISBN 0-201-82653-4
- О'Лири (2003), Структура доказательства: с логикой и теорией множеств , Прентис-Холл
- Лэй (2001), Анализ с введением в доказательство , Прентис Холл
- Мораш, Рональд П. (1987), Мост к абстрактной математике , Random House, ISBN 0-394-35429-Х
- Гилберт; Ванстон (2005), Введение в математическое мышление , Пирсон Прентис-Холл
- Флетчер; Пэтти, Основы высшей математики , PWS-Кент
- Иглевич; Стойл, «Введение в математические рассуждения» , Макмиллан.
- Д'Анджело; Уэст (2000), Математическое мышление: решение проблем и доказательства , Прентис Холл
- Купиллари , Гайки и болты доказательств , Уодсворт
- Бонд, «Введение в абстрактную математику» , Брукс/Коул
- Барнье; Фельдман (2000), Введение в высшую математику , Прентис Холл
- Эш, Букварь абстрактной математики , MAA
Внешние ссылки [ править ]
 СМИ, связанные с классами эквивалентности, на Викискладе?
СМИ, связанные с классами эквивалентности, на Викискладе?





![{\displaystyle [а]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea82bc70a8e322f13a3c4e5b9d5d69e8ef097ad8)
![{\displaystyle [a]_ {\sim }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3906ba39d6194f63cd682c68521fe0b61f18f284)












![{\displaystyle [a]=\{x\in X:a\sim x\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea7485ac987f94badf6d6b3a22866a1fc0d2f151)


![{\displaystyle x\mapsto [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a07b95c49afdb5a84f26120657148e94c94a69be)






![{\displaystyle [х].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00df149bf9dc9b370aecd7bec8c108b37a846117)
![{\displaystyle [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d)
![{\displaystyle [y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f637a17dac262ee0fc8d58e31d08ca3ebe5a0fed)



![{\displaystyle [x]=[y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c34866e2a1216182b168dc1e272b0b02f1aab3a)
![{\displaystyle [x]\cap [y]\neq \emptyset .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2446e8a76d1e403fff2ee153d5dddef4cf1678ce)




![{\displaystyle [7],[9],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/925eb1a9c42148a98f32d5b4c89ea765e57f5381)
![{\displaystyle [1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83021ecdd7307a04dbb7873affcaac031e7e935a)





























