Универсальная собственность

Чтобы узнать о других значениях, см. «Универсальный (значения)» .

Типичная схема определения универсального морфизма.

В математике , точнее в теории категорий , универсальное свойство — это свойство, характеризующее до изоморфизма с точностью результат некоторых построений. Таким образом, универсальные свойства могут быть использованы для определения некоторых объектов независимо от выбранного метода их построения. Например, определения целых чисел из натуральных чисел , рациональных чисел из целых чисел, действительных чисел из рациональных чисел и колец полиномов из поля их коэффициентов — все это можно сделать с точки зрения универсальных свойств. В частности, концепция универсального свойства позволяет просто доказать, что все конструкции действительных чисел эквивалентны: достаточно доказать, что они удовлетворяют одному и тому же универсальному свойству.

Технически универсальное свойство определяется в терминах категорий и функторов посредством универсального морфизма (см. § Формальное определение ниже). Универсальные морфизмы также можно рассматривать более абстрактно как начальные или конечные объекты категории запятой (см. § Связь с категориями запятой ниже).

Универсальные свойства встречаются в математике почти повсюду, и использование этой концепции позволяет использовать общие свойства универсальных свойств для легкого доказательства некоторых свойств, которые в противном случае потребовали бы скучных проверок. Например, для кольца R поле факторкольца частных R ; p по простому идеалу p отождествить с вычетов локализации в R коммутативного точке полем можно то есть $R_{p}/pR_{p}\cong \operatorname {Frac} (R/p)$ (все эти конструкции могут быть определены универсальными свойствами).

Другие объекты, которые могут быть определены универсальными свойствами, включают: все свободные объекты , прямые произведения и прямые суммы , свободные группы , свободные решетки , группу Гротендика , пополнение метрического пространства , пополнение кольца , пополнение Дедекинда – МакНила , топологии произведения , Стоун. – компактификация Чеха , тензорные произведения , обратный предел и прямой предел , ядра и коядра , факторгруппы , фактор-векторные пространства и другие фактор-пространства .

Мотивация

Прежде чем дать формальное определение универсальных свойств, мы предложим некоторую мотивацию для изучения таких конструкций.

• Конкретные детали данной конструкции могут быть беспорядочными, но если конструкция удовлетворяет универсальному свойству, обо всех этих деталях можно забыть: все, что нужно знать о конструкции, уже содержится в универсальном свойстве. Доказательства часто становятся короткими и изящными, если использовать универсальное свойство, а не конкретные детали. Например, тензорную алгебру векторного пространства немного сложно построить, но с ней гораздо проще справиться благодаря ее универсальному свойству.
• Универсальные свойства определяют объекты однозначно с точностью до уникального изоморфизма . Следовательно, одна из стратегий доказательства изоморфности двух объектов — показать, что они удовлетворяют одному и тому же универсальному свойству.
• Универсальные конструкции носят функториальный характер: если можно выполнить построение для каждого объекта категории C, то получается функтор на C . Более того, этот функтор является правым или левым сопряженным функтору U, используемому при определении универсального свойства.
• Универсальные свойства встречаются в математике повсюду. Понимая их абстрактные свойства, можно получить информацию обо всех этих конструкциях и избежать повторения одного и того же анализа для каждого отдельного случая.

Формальное определение

Чтобы понять определение универсальной конструкции, важно рассмотреть примеры. Универсальные конструкции не были определены на пустом месте, а были определены после того, как математики начали замечать закономерности во многих математических конструкциях (см. Примеры ниже). Следовательно, определение может сначала показаться непонятным, но станет ясным, когда вы согласуете его с конкретными примерами.

Позволять $F:{\mathcal {C}}\to {\mathcal {D}}$ быть функтором между категориями ${\mathcal {C}}$ и ${\mathcal {D}}$. В дальнейшем пусть $X$ быть объектом ${\mathcal {D}}$, $A$ и $A'$ быть объектами ${\mathcal {C}}$, и $h:A\to A'$ быть морфизмом в ${\mathcal {C}}$.

Тогда функтор $F$ карты $A$, $A'$ и $h$ в ${\mathcal {C}}$ к $F(A)$, $F(A')$ и $F(h)$ в ${\mathcal {D}}$.

Универсальный морфизм из $X$ к $F$ это уникальная пара $(A,u:X\to F(A))$ в ${\mathcal {D}}$ который обладает следующим свойством, обычно называемым универсальным свойством :

Для любого морфизма вида $f:X\to F(A')$ в ${\mathcal {D}}$, существует единственный морфизм $h:A\to A'$ в ${\mathcal {C}}$ такая, что следующая диаграмма коммутирует :

The typical diagram of the definition of a universal morphism.

Мы можем дуализировать это категориальное понятие. Универсальный морфизм из $F$ к $X$ это уникальная пара $(A,u:F(A)\to X)$ которое удовлетворяет следующему универсальному свойству:

Для любого морфизма вида $f:F(A')\to X$ в ${\mathcal {D}}$, существует единственный морфизм $h:A'\to A$ в ${\mathcal {C}}$ такая, что следующая диаграмма коммутирует:

The most important arrow here is $u:F(A)\to X$ which establishes the universal property.

Обратите внимание, что в каждом определении стрелки перевернуты. Оба определения необходимы для описания универсальных конструкций, возникающих в математике; но они также возникают из-за присущей теории категорий двойственности.В любом случае мы говорим, что пара $(A,u)$ который ведет себя так, как указано выше, удовлетворяет универсальному свойству.

Связь с категориями через запятую

Универсальные морфизмы можно описать более кратко как начальные и конечные объекты в категории запятой (т.е. такой, где морфизмы рассматриваются как самостоятельные объекты).

Позволять $F:{\mathcal {C}}\to {\mathcal {D}}$ быть функтором и $X$ объект ${\mathcal {D}}$. Тогда вспомните, что категория запятой $(X\downarrow F)$ это категория, в которой

• Объекты представляют собой пары формы $(B,f:X\to F(B))$, где $B$ является объектом в ${\mathcal {C}}$
• Морфизм из $(B,f:X\to F(B))$ к $(B',f':X\to F(B'))$ задается морфизмом $h:B\to B'$ в ${\mathcal {C}}$ такая, что диаграмма коммутирует:

A morphism in the comma category is given by the morphism $h:B\to B'$ which also makes the diagram commute.

Теперь предположим, что объект $(A,u:X\to F(A))$ в $(X\downarrow F)$ является начальным. Затемдля каждого объекта $(A',f:X\to F(A'))$, существует единственный морфизм $h:A\to A'$ такая, что следующая диаграмма коммутирует.

This demonstrates the connection between a universal diagram being an initial object in a comma category.

Обратите внимание, что равенство здесь просто означает, что диаграммы одинаковы. Также обратите внимание, что диаграмма в правой части равенства точно такая же, как и диаграмма, предложенная при определении универсального морфизма из $X$ к $F$. Таким образом, мы видим, что универсальный морфизм из $X$ к $F$ эквивалентно исходному объекту в категории запятой $(X\downarrow F)$.

И наоборот, напомним, что категория запятой $(F\downarrow X)$ это категория, в которой

• Объекты представляют собой пары формы $(B,f:F(B)\to X)$ где $B$ является объектом в ${\mathcal {C}}$
• Морфизм из $(B,f:F(B)\to X)$ к $(B',f':F(B')\to X)$ задается морфизмом $h:B\to B'$ в ${\mathcal {C}}$ такая, что диаграмма коммутирует:

This simply demonstrates the definition of a morphism in a comma category.

Предполагать $(A,u:F(A)\to X)$ является терминальным объектом в $(F\downarrow X)$. Тогда для каждого объекта $(A',f:F(A')\to X)$, существует единственный морфизм $h:A'\to A$ такие, что следующие диаграммы коммутируют.

This shows that a terminal object in a specific comma category corresponds to a universal morphism.

Диаграмма в правой части равенства — это та же диаграмма, что и при определении универсального морфизма из $F$ к $X$. Следовательно, универсальный морфизм из $F$ к $X$ соответствует терминальному объекту в категории запятой $(F\downarrow X)$.

Примеры

Ниже приведены несколько примеров, чтобы подчеркнуть общую идею. Читатель может построить множество других примеров, обратившись к статьям, упомянутым во введении.

алгебры

Позволять ${\mathcal {C}}$ — категория векторных пространств $K$-Вект над полем $K$ и пусть ${\mathcal {D}}$ — категория алгебр $K$- Повсюду $K$ (предполагается единым и ассоциативным ). Позволять

$U$ : $K$-Алг → $K$-Вект

быть функтором забывчивости , который присваивает каждой алгебре ее базовое векторное пространство.

Учитывая любое векторное пространство $V$ над $K$ мы можем построить тензорную алгебру $T(V)$. Тензорная алгебра характеризуется тем, что:

«Любая линейная карта из $V$ к алгебре $A$ однозначно продолжается до гомоморфизма алгебры из $T(V)$ к $A$.”

Это утверждение является исходным свойством тензорной алгебры, поскольку выражает тот факт, что пара $(T(V),i)$, где $i:V\to U(T(V))$ — отображение включения, — универсальный морфизм векторного пространства $V$ к функтору $U$.

Поскольку эта конструкция работает для любого векторного пространства $V$, мы заключаем, что $T$ является функтором из $K$-Вект к $K$-Алг . Это означает, что $T$ остается сопряженным с забывчивым функтором $U$ (см. раздел ниже о сопряженных функторах ).

Продукты

Категориальный продукт можно охарактеризовать универсальной конструкцией. Для конкретности можно рассмотреть декартово произведение в Set , прямое произведение в Grp или топологию произведения в Top , где продукты существуют.

Позволять $X$ и $Y$ быть объектами категории ${\mathcal {C}}$ с конечными произведениями. Продукт $X$ и $Y$ это объект $X$ × $Y$ вместе с двумя морфизмами

$\pi _{1}$ : $X\times Y\to X$

$\pi _{2}$ : $X\times Y\to Y$

такое, что для любого другого объекта $Z$ из ${\mathcal {C}}$ и морфизмы $f:Z\to X$ и $g:Z\to Y$ существует единственный морфизм $h:Z\to X\times Y$ такой, что $f=\pi _{1}\circ h$ и $g=\pi _{2}\circ h$.

Чтобы понять эту характеристику как универсальное свойство, возьмем категорию ${\mathcal {D}}$ быть категорией продукта ${\mathcal {C}}\times {\mathcal {C}}$ и определим диагональный функтор

$\Delta :{\mathcal {C}}\to {\mathcal {C}}\times {\mathcal {C}}$

к $\Delta (X)=(X,X)$ и $\Delta (f:X\to Y)=(f,f)$. Затем $(X\times Y,(\pi _{1},\pi _{2}))$ является универсальным морфизмом из $\Delta$ на объект $(X,Y)$ из ${\mathcal {C}}\times {\mathcal {C}}$: если $(f,g)$ любой морфизм из $(Z,Z)$ к $(X,Y)$, то оно должно быть равноморфизм $\Delta (h:Z\to X\times Y)=(h,h)$ от $\Delta (Z)=(Z,Z)$к $\Delta (X\times Y)=(X\times Y,X\times Y)$ с последующим $(\pi _{1},\pi _{2})$. В качестве коммутативной диаграммы:

Commutative diagram showing how products have a universal property.

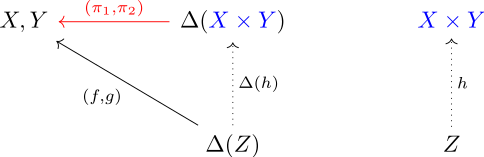
На примере декартова произведения в Set морфизм $(\pi _{1},\pi _{2})$ включает в себя две проекции $\pi _{1}(x,y)=x$ и $\pi _{2}(x,y)=y$. Учитывая любой набор $Z$ и функции $f,g$ единственное отображение такое, что требуемая диаграмма коммутирует, имеет вид $h=\langle x,y\rangle (z)=(f(z),g(z))$.

Пределы и копределы

Категориальные продукты представляют собой особый вид предела в теории категорий. Приведенный выше пример можно обобщить на произвольные пределы и копределы.

Позволять ${\mathcal {J}}$ и ${\mathcal {C}}$ быть категориями с ${\mathcal {J}}$ небольшую пусть индексную категорию и ${\mathcal {C}}^{\mathcal {J}}$ — соответствующая категория функтора . Диагональный функтор

$\Delta :{\mathcal {C}}\to {\mathcal {C}}^{\mathcal {J}}$

это функтор, который отображает каждый объект $N$ в ${\mathcal {C}}$ к постоянному функтору $\Delta (N):{\mathcal {J}}\to {\mathcal {C}}$ (т.е. $\Delta (N)(X)=N$ для каждого $X$ в ${\mathcal {J}}$ и $\Delta (N)(f)=1_{N}$ для каждого $f:X\to Y$ в ${\mathcal {J}}$) и каждый морфизм $f:N\to M$ в ${\mathcal {C}}$ к естественной трансформации $\Delta (f):\Delta (N)\to \Delta (M)$ в ${\mathcal {C}}^{\mathcal {J}}$ определяется как для каждого объекта $X$ из ${\mathcal {J}}$, компонент

$$\Delta (f)(X):\Delta (N)(X)\to \Delta (M)(X)=f:N\to M$$

в $X$. Другими словами, естественное преобразование определяется наличием постоянной составляющей. $f:N\to M$ для каждого объекта ${\mathcal {J}}$.

Учитывая функтор $F:{\mathcal {J}}\to {\mathcal {C}}$ (думается как объект в ${\mathcal {C}}^{\mathcal {J}}$ , предел ) $F$, если он существует, есть не что иное, как универсальный морфизм из $\Delta$ к $F$. , копредел Двойственно $F$ является универсальным морфизмом из $F$ к $\Delta$.

Свойства

Существование и уникальность

Определение количества не гарантирует его существования. Учитывая функтор $F:{\mathcal {C}}\to {\mathcal {D}}$ и объект $X$ из ${\mathcal {D}}$, может существовать или не существовать универсальный морфизм из $X$ к $F$. Если же универсальный морфизм $(A,u)$ существует, то оно по существу уникально. В частности, он уникален до единственного с точностью изоморфизма : если $(A',u')$ другая пара, то существует единственный изоморфизм $k:A\to A'$ такой, что $u'=F(k)\circ u$.В этом легко убедиться, подставив $(A,u')$ в определении универсального морфизма.

Это пара $(A,u)$ что по сути уникально в этом смысле. Объект $A$ сам по себе уникален только с точностью до изоморфизма. Действительно, если $(A,u)$ является универсальным морфизмом и $k:A\to A'$ является любым изоморфизмом, то пара $(A',u')$, где $u'=F(k)\circ u$ также является универсальным морфизмом.

составы

Определение универсального морфизма можно перефразировать по-разному. Позволять $F:{\mathcal {C}}\to {\mathcal {D}}$ быть функтором и пусть $X$ быть объектом ${\mathcal {D}}$. Тогда следующие утверждения эквивалентны:

• $(A,u)$ является универсальным морфизмом из $X$ к $F$
• $(A,u)$ является исходным объектом категории запятая $(X\downarrow F)$
• $(A,F(\bullet )\circ u)$ является представлением ​ ${\text{Hom}}_{\mathcal {D}}(X,F(-))$, где его компоненты $(F(\bullet )\circ u)_{B}:{\text{Hom}}_{\mathcal {C}}(A,B)\to {\text{Hom}}_{\mathcal {D}}(X,F(B))$ определяются

$$(F(\bullet )\circ u)_{B}(f:A\to B):X\to F(B)=F(f)\circ u:X\to F(B)$$

для каждого объекта $B$ в ${\mathcal {C}}.$

Двойные утверждения также эквивалентны:

• $(A,u)$ является универсальным морфизмом из $F$ к $X$
• $(A,u)$ является терминальным объектом категории запятой $(F\downarrow X)$
• $(A,u\circ F(\bullet ))$ является представлением ${\text{Hom}}_{\mathcal {D}}(F(-),X)$, где его компоненты $(u\circ F(\bullet ))_{B}:{\text{Hom}}_{\mathcal {C}}(B,A)\to {\text{Hom}}_{\mathcal {D}}(F(B),X)$ определяются

$$(u\circ F(\bullet ))_{B}(f:B\to A):F(B)\to X=u\circ F(f):F(B)\to X$$

для каждого объекта $B$ в ${\mathcal {C}}.$

с

Предполагать $(A_{1},u_{1})$ является универсальным морфизмом из $X_{1}$ к $F$ и $(A_{2},u_{2})$ является универсальным морфизмом из $X_{2}$ к $F$. По универсальному свойству универсальных морфизмов для любого морфизма $h:X_{1}\to X_{2}$ существует единственный морфизм $g:A_{1}\to A_{2}$ такая, что следующая диаграмма коммутирует:

Universal morphisms can behave like a natural transformation between functors under suitable conditions.

Если каждый объект $X_{i}$ из ${\mathcal {D}}$ допускает универсальный морфизм $F$, то задание $X_{i}\mapsto A_{i}$ и $h\mapsto g$ определяет функтор $G:{\mathcal {D}}\to {\mathcal {C}}$. Карты $u_{i}$ затем определим естественное преобразование из $1_{\mathcal {D}}$ (тождественный функтор на ${\mathcal {D}}$) к $F\circ G$. Функторы $(F,G)$ тогда являются парой сопряженных функторов с $G$ левосопряженный к $F$ и $F$ правосопряженный к $G$.

Аналогичные утверждения применимы и к двойственной ситуации терминальных морфизмов из $F$. Если такие морфизмы существуют для каждого $X$ в ${\mathcal {C}}$ получается функтор $G:{\mathcal {C}}\to {\mathcal {D}}$ который правосопряжён к $F$ (так $F$ является левосопряженным к $G$).

Действительно, все пары сопряженных функторов возникают таким образом из универсальных конструкций. Позволять $F$ и $G$ быть парой сопряженных функторов с единицей $\eta$ и со-юнит $\epsilon$ (определения см. в статье о сопряженных функторах ). Тогда у нас есть универсальный морфизм для каждого объекта в ${\mathcal {C}}$ и ${\mathcal {D}}$:

• Для каждого объекта $X$ в ${\mathcal {C}}$, $(F(X),\eta _{X})$ является универсальным морфизмом из $X$ к $G$. То есть для всех $f:X\to G(Y)$ существует уникальный $g:F(X)\to Y$ для которых коммутируют следующие диаграммы.
• Для каждого объекта $Y$ в ${\mathcal {D}}$, $(G(Y),\epsilon _{Y})$ является универсальным морфизмом из $F$ к $Y$. То есть для всех $g:F(X)\to Y$ существует уникальный $f:X\to G(Y)$ для которых коммутируют следующие диаграммы.

The unit and counit of an adjunction, which are natural transformations between functors, are an important example of universal morphisms.

Универсальные конструкции более общие, чем пары сопряженных функторов: универсальная конструкция подобна задаче оптимизации; она порождает сопряженную пару тогда и только тогда, когда эта задача имеет решение для каждого объекта ${\mathcal {C}}$ (эквивалентно, каждый объект ${\mathcal {D}}$).

История

Универсальные свойства различных топологических конструкций были представлены Пьером Самуэлем в 1948 году. Позже они широко использовались Бурбаки . Близко связанная концепция сопряженных функторов была независимо введена Дэниелом Каном в 1958 году.

См. также

• Бесплатный объект
• Естественная трансформация
• Сопряженный функтор
• Монада (теория категорий)
• Разнообразие алгебр
• Декартова закрытая категория

Ссылки

• Пол Кон , Универсальная алгебра (1981), D.Reidel Publishing, Голландия. ISBN   90-277-1213-1 .
• Мак Лейн, Сондерс (1998). Категории для работающего математика . Тексты для аспирантов по математике 5 (2-е изд.). Спрингер. ISBN  0-387-98403-8 .
• Борсо, Ф. Справочник по категориальной алгебре: том 1 Основная теория категорий (1994) Издательство Кембриджского университета, (Энциклопедия математики и ее приложений) ISBN   0-521-44178-1
• Н. Бурбаки, Книга II: Алгебра (1970), Герман, ISBN   0-201-00639-1 .
• Милиес, Сезар Польчино; Сегал, Сударшан К.. Введение в групповые кольца . Алгебры и приложения, Том 1. Springer, 2002. ISBN   978-1-4020-0238-0
• Джейкобсон. Основная алгебра II. Дувр. 2009. ISBN   0-486-47187-X

Внешние ссылки

• nLab — вики-проект по математике, физике и философии с упором на n -категориальную точку зрения.
• Андре Жойал , CatLab , вики-проект, посвященный изложению категориальной математики.
• Хиллман, Крис (2001). Категорический учебник . CiteSeerX   10.1.1.24.3264 : формальное введение в теорию категорий.
• Дж. Адамек, Х. Херрлих, Г. Стекер, Абстрактные и конкретные категории – радость кошек
• Стэнфордская энциклопедия философии : « Теория категорий » Жан-Пьера Маркиза. Обширная библиография.
• Список научных конференций по теории категорий
• Баэз, Джон, 1996, « Повесть о n -категориях». Неофициальное введение в категории высшего порядка.
• WildCats — это пакет теории категорий для Mathematica . Манипулирование и визуализация объектов, морфизмов , категорий, функторов , естественных преобразований , универсальных свойств .
• The catsters — канал на YouTube, посвященный теории категорий.
• Видеоархив записей выступлений по категориям, логике и основам физики.
• Интерактивная веб-страница , генерирующая примеры категориальных конструкций в категории конечных множеств.