Изображение (теория категорий)

В теории категорий математики , образ морфизма является разделе обобщением образа функции , .

Общее определение [ править ]

Учитывая категорию $C$ и морфизм $f\colon X\to Y$ в $C$ , изображение ^[1]из $f$ является мономорфизмом $m\colon I\to Y$ удовлетворяющее следующему универсальному свойству :

Существует морфизм $e\colon X\to I$ такой, что $f=m\,e$ .
Для любого объекта $I'$ с морфизмом $e'\colon X\to I'$ и мономорфизм $m'\colon I'\to Y$ такой, что $f=m'\,e'$ , существует единственный морфизм $v\colon I\to I'$ такой, что $m=m'\,v$ .

Примечания:

такая факторизация не обязательно существует.
$e$ уникален по определению $m$ Моника .
$m'e'=f=me=m've$ , поэтому $e'=ve$ к $m'$ Моника.
$v$ моник.
$m=m'\,v$ уже подразумевает, что $v$ является уникальным.

Образ $f$ часто обозначается ${\text{Im}}f$ или ${\text{Im}}(f)$ .

Предложение: Если $C$ есть все эквалайзеры, то $e$ в факторизации $f=m\,e$ (1) является эпиморфизмом . ^[2]

Доказательство

Позволять $\alpha ,\,\beta$ быть таким, что $\alpha \,e=\beta \,e$ , нужно это показать $\alpha =\beta$ . Так как эквалайзер $(\alpha ,\beta )$ существует, $e$ факторизуется как $e=q\,e'$ с $q$ моник. Но тогда $f=(m\,q)\,e'$ представляет собой факторизацию $f$ с $(m\,q)$ мономорфизм. Следовательно, по универсальному свойству изображения существует единственная стрелка $v:I\to Eq_{\alpha ,\beta }$ такой, что $m=m\,q\,v$ и поскольку $m$ моник ${\text{id}}_{I}=q\,v$ . Кроме того, у человека есть $m\,q=(mqv)\,q$ и по свойству мономорфизма $mq$ получается ${\text{id}}_{Eq_{\alpha ,\beta }}=v\,q$ .

Это означает, что $I\equiv Eq_{\alpha ,\beta }$ и таким образом, что ${\text{id}}_{I}=q\,v$ уравнивает $(\alpha ,\beta )$ , откуда $\alpha =\beta$ .

Второе определение [ править ]

В категории $C$ со всеми конечными и копределами изображение определяется пределами как эквалайзер $(Im,m)$ так называемой пары коядер $(Y\sqcup _{X}Y,i_{1},i_{2})$ , который является кокартезианом морфизма самого себя в своей области определения, что приведет к паре морфизмов $i_{1},i_{2}:Y\to Y\sqcup _{X}Y$ , на котором взят уравнитель , т.е. первая из следующих диаграмм кокартова , а вторая уравнивающая . ^[3]

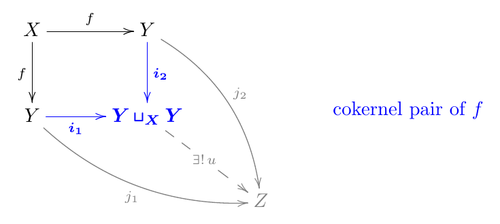
Примечания:

Конечная биполнота категории обеспечивает существование пушаутов и эквалайзеров.
$(Im,m)$ можно назвать обычным изображением как $m$ — регулярный мономорфизм , т. е. эквалайзер пары морфизмов. (Напомним также, что эквалайзер автоматически является мономорфизмом).
В абелевой категории свойство пары коядер можно записать $i_{1}\,f=i_{2}\,f\ \Leftrightarrow \ (i_{1}-i_{2})\,f=0=0\,f$ и условие эквалайзера $i_{1}\,m=i_{2}\,m\ \Leftrightarrow \ (i_{1}-i_{2})\,m=0\,m$ . Более того, все мономорфизмы регулярны.

Теорема — Если $f$ всегда факторизуется посредством регулярных мономорфизмов, то два определения совпадают.

Доказательство

Из первого определения следует второе: предположим, что (1) выполнено при $m$ регулярный мономорфизм.

Уравнивание: нужно показать, что $i_{1}\,m=i_{2}\,m$ . Поскольку пара коядер $f,\ i_{1}\,f=i_{2}\,f$ и по предыдущему предложению, поскольку $C$ есть все эквалайзеры, стрелка $e$ в факторизации $f=m\,e$ является эпиморфизмом , следовательно, $i_{1}\,f=i_{2}\,f\ \Rightarrow \ i_{1}\,m=i_{2}\,m$ .
Универсальность: в категории со всеми копределами (или хотя бы со всеми выталкиваниями) $m$ сам допускает пару коядер $(Y\sqcup _{I}Y,c_{1},c_{2})$

Более того, как регулярный мономорфизм

(I,m)

является эквалайзером пары морфизмов

b_{1},b_{2}:Y\longrightarrow B

но мы утверждаем здесь, что это также эквалайзер

c_{1},c_{2}:Y\longrightarrow Y\sqcup _{I}Y

.

Действительно, по построению

b_{1}\,m=b_{2}\,m

таким образом, диаграмма «пары коядер» для

m

дает уникальный морфизм

u':Y\sqcup _{I}Y\longrightarrow B

такой, что

b_{1}=u'\,c_{1},\ b_{2}=u'\,c_{2}

. Теперь карта

m':I'\longrightarrow Y

который уравнивает

(c_{1},c_{2})

также удовлетворяет

b_{1}\,m'=u'\,c_{1}\,m'=u'\,c_{2}\,m'=b_{2}\,m'

, следовательно, по диаграмме эквалайзера для

(b_{1},b_{2})

, существует единственное отображение

h':I'\to I

такой, что

m'=m\,h'

.

Наконец, используйте диаграмму пар коядер (из

f

) с

j_{1}:=c_{1},\ j_{2}:=c_{2},\ Z:=Y\sqcup _{I}Y

: существует уникальный

u:Y\sqcup _{X}Y\longrightarrow Y\sqcup _{I}Y

такой, что

c_{1}=u\,i_{1},\ c_{2}=u\,i_{2}

. Поэтому любая карта

g

который уравнивает

(i_{1},i_{2})

также уравнивает

(c_{1},c_{2})

и, таким образом, однозначно факторизуется как

g=m\,h'

. Это именно означает, что

(I,m)

это эквалайзер

(i_{1},i_{2})

.

Второе определение подразумевает первое:

Факторизация: взятие $m':=f$ на схеме эквалайзера ( $m'$ соответствует $g$ ), получаем факторизацию $f=m\,h$ .
Универсальность: пусть $f=m'\,e'$ быть факторизацией с $m'$ регулярный мономорфизм, т.е. эквалайзер некоторой пары $(d_{1},d_{2})$ .

Затем

d_{1}\,m'=d_{2}\,m'\ \Rightarrow \ d_{1}\,f=d_{1}\,m'\,e=d_{2}\,m'\,e=d_{2}\,f

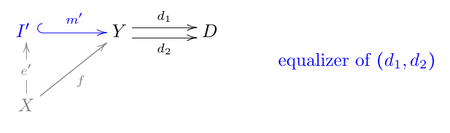
так что по диаграмме «пара коядер» (из

f

), с

j_{1}:=d_{1},\ j_{2}:=d_{2},\ Z:=D

, существует уникальный

u'':Y\sqcup _{X}Y\longrightarrow D

такой, что

d_{1}=u''\,i_{1},\ d_{2}=u''\,i_{2}

.

Теперь из

i_{1}\,m=i_{2}\,m

( m из эквалайзера диаграммы ( i ₁ , i ₂ )), получаем

d_{1}\,m=u''\,i_{1}\,m=u''\,i_{2}\,m=d_{2}\,m

, следовательно, в силу универсальности в диаграмме (эквалайзер ( d ₁ , d ₂ ) с заменой f на m ) существует единственный

v:Im\longrightarrow I'

такой, что

m=m'\,v

.

Примеры [ править ]

В категории множеств образ морфизма $f\colon X\to Y$ это включение из обычного изображения $\{f(x)~|~x\in X\}$ к $Y$ . Во многих конкретных категориях, таких как группы , абелевы группы и (левые или правые) модули , образ морфизма является образом соответствующего морфизма в категории множеств.

В любой нормальной категории с нулевым объектом и ядрами и коядрами для каждого морфизма образ морфизма $f$ можно выразить следующим образом:

im f = ker coker f

В абелевой категории (которая, в частности, является бинормальной), если f — мономорфизм, то f = ker coker f , и поэтому f = im f .

См. также [ править ]

Ссылки [ править ]

^ Митчелл, Барри (1965), Теория категорий , Чистая и прикладная математика, том. 17, Академическое издательство, ISBN 978-0-12-499250-4 , МР 0202787 Раздел I.10 стр.12
^ Митчелл, Барри (1965), Теория категорий , Чистая и прикладная математика, том. 17, Академическое издательство, ISBN 978-0-12-499250-4 , МР 0202787 Предложение 10.1 п.12
^ Касивара, Масаки ; Шапира, Пьер (2006), «Категории и пучки» , Основы математических наук, том. 332, Берлин Гейдельберг: Springer, стр. 113–114. Определение 5.1.1.

[1] Митчелл, Барри (1965), Теория категорий , Чистая и прикладная математика, том. 17, Академическое издательство, ISBN 978-0-12-499250-4 , МР 0202787 Раздел I.10 стр.12

[2] Митчелл, Барри (1965), Теория категорий , Чистая и прикладная математика, том. 17, Академическое издательство, ISBN 978-0-12-499250-4 , МР 0202787 Предложение 10.1 п.12

[3] Касивара, Масаки ; Шапира, Пьер (2006), «Категории и пучки» , Основы математических наук, том. 332, Берлин Гейдельберг: Springer, стр. 113–114. Определение 5.1.1.

[1]

[2]

[3]