Алгоритм собственных значений «разделяй и властвуй»

Алгоритмы собственных значений «разделяй и властвуй» — это класс алгоритмов собственных значений для эрмитовых или действительных симметричных матриц , которые в последнее время (около 1990-х годов) стали конкурентоспособными с точки зрения стабильности и эффективности с более традиционными алгоритмами, такими как алгоритм QR . Основная концепция этих алгоритмов — подход «разделяй и властвуй» из информатики . Проблема собственных значений делится на две проблемы примерно вдвое меньшего размера, каждая из которых решается рекурсивно , а собственные значения исходной проблемы вычисляются на основе результатов этих меньших задач.

В этой статье рассматривается основная идея алгоритма, первоначально предложенного Куппеном в 1981 году, который не является численно стабильным без дополнительных уточнений.

Фон

Как и в большинстве алгоритмов собственных значений для эрмитовых матриц, принцип «разделяй и властвуй» начинается с приведения к трехдиагональной форме. Для $m\times m$ матрица, стандартный метод для этого, через отражения Хаусхолдера , принимает ${\frac {4}{3}}m^{3}$ операции с плавающей запятой или ${\frac {8}{3}}m^{3}$ если собственные векторы также нужны . Существуют и другие алгоритмы, такие как итерация Арнольди , которые могут работать лучше для определенных классов матриц; мы не будем рассматривать это далее здесь.

В некоторых случаях можно разложить проблему собственных значений на более мелкие задачи. Рассмотрим блочную диагональную матрицу

$T={\begin{bmatrix}T_{1}&0\\0&T_{2}\end{bmatrix}}.$

Собственные значения и собственные векторы $T$ являются просто теми из $T_{1}$ и $T_{2}$, и почти всегда будет быстрее решить эти две меньшие проблемы, чем решить исходную проблему сразу. Этот метод можно использовать для повышения эффективности многих алгоритмов собственных значений, но он имеет особое значение для принципа «разделяй и властвуй».

В оставшейся части статьи мы будем предполагать, что входными данными для алгоритма «разделяй и властвуй» являются $m\times m$ действительная симметричная трехдиагональная матрица $T$. Алгоритм может быть модифицирован для эрмитовых матриц.

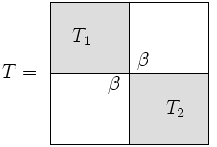
Разделять

Часть алгоритма « разделяй и властвуй» исходит из осознания того, что трехдиагональная матрица является «почти» диагональю блока.

Размер подматрицы $T_{1}$ мы позвоним $n\times n$, а потом $T_{2}$ является $(m-n)\times (m-n)$. $T$ почти блочная диагональ, независимо от того, как $n$ выбран. Для эффективности мы обычно выбираем $n\approx m/2$.

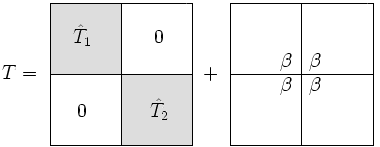
Мы пишем $T$ как блочная диагональная матрица плюс поправка ранга 1 :

Единственная разница между $T_{1}$ и ${\hat {T}}_{1}$ это правая нижняя запись $t_{nn}$ в ${\hat {T}}_{1}$ был заменен на $t_{nn}-\beta$ и аналогично, в ${\hat {T}}_{2}$ верхняя левая запись $t_{n+1,n+1}$ был заменен на $t_{n+1,n+1}-\beta$.

Оставшаяся часть шага деления заключается в поиске собственных значений (и, при желании, собственных векторов) ${\hat {T}}_{1}$ и ${\hat {T}}_{2}$, то есть найти диагонализации ${\hat {T}}_{1}=Q_{1}D_{1}Q_{1}^{T}$ и ${\hat {T}}_{2}=Q_{2}D_{2}Q_{2}^{T}$. Этого можно добиться с помощью рекурсивных вызовов алгоритма «разделяй и властвуй», хотя практические реализации часто переключаются на алгоритм QR для достаточно маленьких подматриц.

Завоевывать

Часть направленная на завоевание, алгоритма, является неинтуитивной частью. Учитывая вычисленные выше диагонализации подматриц, как найти диагонализацию исходной матрицы?

Сначала определите $z^{T}=(q_{1}^{T},q_{2}^{T})$, где $q_{1}^{T}$ это последний ряд $Q_{1}$ и $q_{2}^{T}$ это первый ряд $Q_{2}$. Теперь элементарно показать, что

$T={\begin{bmatrix}Q_{1}&\\&Q_{2}\end{bmatrix}}\left({\begin{bmatrix}D_{1}&\\&D_{2}\end{bmatrix}}+\beta zz^{T}\right){\begin{bmatrix}Q_{1}^{T}&\\&Q_{2}^{T}\end{bmatrix}}$

Оставшаяся задача свелась к нахождению собственных значений диагональной матрицы плюс поправки первого ранга. Прежде чем показать, как это сделать, упростим обозначения. Ищем собственные значения матрицы $D+ww^{T}$, где $D$ диагональная с различными элементами и $w$ — любой вектор с ненулевыми элементами. В этом случае $w={\sqrt {|\beta |}}\cdot z$.

Случай нулевой записи прост, поскольку если w _i равно нулю, ( $e_{i}$,d _i ) является собственной парой ( $e_{i}$ находится в стандартном базисе) $D+ww^{T}$ с $(D+ww^{T})e_{i}=De_{i}=d_{i}e_{i}$.

Если $\lambda$ является собственным значением, мы имеем:

$(D+ww^{T})q=\lambda q$

где $q$ — соответствующий собственный вектор. Сейчас

$(D-\lambda I)q+w(w^{T}q)=0$

$q+(D-\lambda I)^{-1}w(w^{T}q)=0$

$w^{T}q+w^{T}(D-\lambda I)^{-1}w(w^{T}q)=0$

Имейте в виду, что $w^{T}q$ является ненулевым скаляром. Ни один $w$ ни $q$ равны нулю. Если $w^{T}q$ должно было быть равно нулю, $q$ будет собственным вектором $D$ к $(D+ww^{T})q=\lambda q$. Если бы это было так, $q$ будет содержать только одну ненулевую позицию, поскольку $D$ является отличной диагональю и, следовательно, внутренним произведением $w^{T}q$ ведь не может быть нулем. Таким образом, мы имеем:

$1+w^{T}(D-\lambda I)^{-1}w=0$

или записанное в виде скалярного уравнения,

$1+\sum _{j=1}^{m}{\frac {w_{j}^{2}}{d_{j}-\lambda }}=0.$

Это уравнение известно как вековое уравнение . Таким образом, задача свелась к нахождению корней рациональной функции, определяемой левой частью этого уравнения.

Все общие алгоритмы собственных значений должны быть итеративными. и алгоритм «разделяй и властвуй» ничем не отличается. Решение нелинейного векового уравнения требует итерационного метода, такого как метод Ньютона-Рафсона . Однако каждый корень можно найти за O (1) итераций, каждая из которых требует $\Theta (m)$ проваливается (для $m$-степень рациональной функции), что делает стоимость итеративной части этого алгоритма $\Theta (m^{2})$.

Анализ

W будет использовать основную теорему для повторений по принципу «разделяй и властвуй» для анализа времени выполнения. Помните, что выше мы заявили, что выбираем $n\approx m/2$. Мы можем написать рекуррентное соотношение :

$T(m)=2\times T\left({\frac {m}{2}}\right)+\Theta (m^{2})$

В обозначениях Мастер-теоремы $a=b=2$ и таким образом $\log _{b}a=1$. Четко, $\Theta (m^{2})=\Omega (m^{1})$, поэтому у нас есть

$T(m)=\Theta (m^{2})$

Выше мы указывали, что приведение эрмитовой матрицы к трехдиагональному виду требует ${\frac {4}{3}}m^{3}$ проваливается. Это затмевает время выполнения части «разделяй и властвуй», и на данный момент неясно, какое преимущество предлагает алгоритм «разделяй и властвуй» перед алгоритмом QR (который также требует $\Theta (m^{2})$ флопы для трехдиагональных матриц).

Преимущество метода «разделяй и властвуй» проявляется тогда, когда также необходимы собственные векторы. В этом случае приведение к трехдиагональной форме принимает ${\frac {8}{3}}m^{3}$, но вторая часть алгоритма занимает $\Theta (m^{3})$ также. Для алгоритма QR с разумной целевой точностью это $\approx 6m^{3}$, тогда как для принципа «разделяй и властвуй» это $\approx {\frac {4}{3}}m^{3}$. Причина такого улучшения заключается в том, что в методе «разделяй и властвуй» $\Theta (m^{3})$ часть алгоритма (умножение $Q$ матрицы) отделены от итерации, тогда как в QR это должно происходить на каждом итерационном шаге. Добавление ${\frac {8}{3}}m^{3}$ провалы для снижения, общее улучшение составляет от $\approx 9m^{3}$ к $\approx 4m^{3}$ проваливается.

Практическое использование алгоритма «разделяй и властвуй» показало, что в большинстве реалистичных задач на собственные значения этот алгоритм действительно справляется лучше. Причина в том, что очень часто матрицы $Q$ и векторы $z$ имеют тенденцию быть численно разреженными , что означает, что они имеют много записей со значениями, меньшими, чем точность с плавающей запятой , что допускает численное дефлятирование , т.е. разбиение проблемы на несвязанные подзадачи.

Варианты и реализация

Представленный здесь алгоритм является самой простой версией. Во многих практических реализациях для обеспечения стабильности используются более сложные поправки ранга 1; в некоторых вариантах даже используются поправки второго ранга.

Существуют специализированные методы поиска корней для рациональных функций, которые могут оказаться лучше, чем метод Ньютона-Рафсона, с точки зрения производительности и стабильности. Их можно использовать для улучшения итеративной части алгоритма «разделяй и властвуй».

Алгоритм «разделяй и властвуй» легко распараллеливается , а пакеты вычислений линейной алгебры, такие как LAPACK, содержат высококачественные параллельные реализации.

Ссылки

• Деммель, Джеймс В. (1997), Прикладная числовая линейная алгебра , Филадельфия, Пенсильвания: Общество промышленной и прикладной математики , ISBN  0-89871-389-7 , МР   1463942 .
• Куппен, JJM (1981). «Метод разделяй и властвуй для решения симметричной трехдиагональной собственной задачи». Численная математика . 36 (2): 177–195. дои : 10.1007/BF01396757 . S2CID   120504744 .