Квадратура параболы

Параболический сегмент.

Квадратура Параболы ( греч . Τετραγωνισμὸς παραβολῆς ) — трактат по геометрии , написанный Архимедом в III веке до нашей эры и адресованный его александрийскому знакомому Досифею. Он содержит 24 утверждения относительно парабол , кульминацией которых являются два доказательства, показывающие, что площадь параболического сегмента (область, ограниченная параболой и линией ) равна ${\tfrac {4}{3}}$ у некоторого вписанного треугольника .

Это одна из самых известных работ Архимеда, в частности благодаря изобретательному использованию метода исчерпания и второй части геометрического ряда . Архимед разбивает эту площадь на бесконечное число треугольников , площади которых образуют геометрическую прогрессию . Затем он вычисляет сумму полученной геометрической прогрессии и доказывает, что это площадь параболического сегмента. Это представляет собой наиболее изощренное использование аргумента доведения до абсурда в древнегреческой математике , и решение Архимеда оставалось непревзойденным до развития интегрального исчисления в 17 веке, на смену которому пришла квадратурная формула Кавальери .

Основная теорема

Параболический сегмент — это область, ограниченная параболой и линией. Чтобы найти площадь сегмента параболы, Архимед рассматривает некий вписанный треугольник. Основание этого треугольника — заданная хорда параболы, а третья вершина — это точка параболы, касательная к параболе в этой точке параллельна хорде. Предложение 1 работы гласит, что линия из третьей вершины, проведенная параллельно оси, делит хорду на равные отрезки. Основная теорема утверждает, что площадь параболического сегмента равна ${\tfrac {4}{3}}$ что и вписанный треугольник.

Структура текста

Первое доказательство Архимедом площади параболического сегмента.

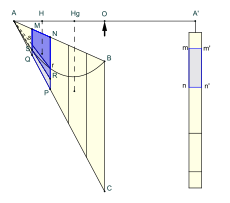
Конические сечения , такие как парабола, были уже хорошо известны во времена Архимеда благодаря Менехму столетием ранее. Однако до появления дифференциального и интегрального исчисления не существовало простых способов найти площадь конического сечения. Архимед предлагает первое подтвержденное решение этой проблемы, сосредоточив особое внимание на области, ограниченной параболой и хордой.

Архимед дает два доказательства основной теоремы: одно с использованием абстрактной механики , а другое — с помощью чистой геометрии. В первом доказательстве Архимед рассматривает рычаг, находящийся в равновесии под действием силы тяжести, с утяжеленными отрезками параболы и треугольника, подвешенными вдоль плеч рычага на определенных расстояниях от точки опоры. Когда известен центр тяжести треугольника, равновесие рычага дает площадь параболы через площадь треугольника, имеющего то же основание и равную высоту. Архимед здесь отклоняется от процедуры, найденной в «О равновесии плоскостей», тем, что у него центры тяжести находятся на уровне ниже уровня баланса. Второе и более известное доказательство использует чистую геометрию, в частности сумму геометрической прогрессии.

Из двадцати четырех предложений первые три цитируются без доказательства из Евклида » «Началов коники (утерянный труд Евклида о конических сечениях ). Предложения 4 и 5 устанавливают элементарные свойства параболы. Предложения 6–17 дают механическое доказательство основной теоремы; предложения 18–24 представляют собой геометрическое доказательство.

Геометрическое доказательство

Второе доказательство Архимеда делит площадь на произвольное количество треугольников.

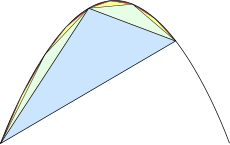
Рассечение параболического сегмента

Основная идея доказательства — разбиение отрезка параболы на бесконечное число треугольников, как показано на рисунке справа. Каждый из этих треугольников вписан в свой отрезок параболы точно так же, как синий треугольник вписан в большой отрезок.

Площади треугольников

В предложениях с восемнадцатого по двадцать первое Архимед доказывает, что площадь каждого зеленого треугольника равна ${\tfrac {1}{8}}$ площадь синего треугольника, так что сумма обоих зеленых треугольников равна ${\tfrac {1}{4}}$ площадь синего треугольника. С современной точки зрения, это потому, что зеленый треугольник имеет ${\tfrac {1}{2}}$ ширина и ${\tfrac {1}{4}}$ высота синего треугольника:

Следуя тому же аргументу, каждый из $4$ желтые треугольники есть ${\tfrac {1}{8}}$ площадь зеленого треугольника или ${\tfrac {1}{64}}$ площадь синего треугольника, равная ${\tfrac {4}{64}}={\tfrac {1}{16}}$ площадь синего треугольника; каждый из $2^{3}=8$ красные треугольники есть ${\tfrac {1}{8}}$ площадь желтого треугольника, равная в сумме ${\tfrac {2^{3}}{8^{3}}}={\tfrac {1}{64}}$ площадь синего треугольника; и т. д. Используя метод исчерпывания , следует, что общая площадь параболического сегмента определяется выражением

${\text{Area}}\;=\;T\,+\,{\frac {1}{4}}T\,+\,{\frac {1}{4^{2}}}T\,+\,{\frac {1}{4^{3}}}T\,+\,\cdots .$

Здесь T представляет площадь большого синего треугольника, второй член представляет собой общую площадь двух зеленых треугольников, третий член представляет собой общую площадь четырех желтых треугольников и так далее. Это упрощает предоставление

${\text{Area}}\;=\;\left(1\,+\,{\frac {1}{4}}\,+\,{\frac {1}{16}}\,+\,{\frac {1}{64}}\,+\,\cdots \right)T.$

Сумма ряда

Доказательство Архимеда, что 1 / 4 + 1 / 16 + 1 / 64 + ⋯ = 1 / 3

Для завершения доказательства Архимед показывает, что

$1\,+\,{\frac {1}{4}}\,+\,{\frac {1}{16}}\,+\,{\frac {1}{64}}\,+\,\cdots \;=\;{\frac {4}{3}}.$

Приведенная выше формула представляет собой геометрическую прогрессию : каждый последующий член равен одной четверти предыдущего члена. В современной математике эта формула является частным случаем формулы суммы геометрической прогрессии .

Архимед вычисляет сумму, используя полностью геометрический метод: показано на соседнем рисунке. На этом рисунке изображен единичный квадрат, разделенный на бесконечное количество меньших квадратов. Площадь каждого последующего фиолетового квадрата составляет одну четверть площади предыдущего квадрата, при этом общая площадь фиолетового цвета равна сумме

${\frac {1}{4}}\,+\,{\frac {1}{16}}\,+\,{\frac {1}{64}}\,+\,\cdots .$

Однако фиолетовые квадраты соответствуют любому набору желтых квадратов и, таким образом, покрывают ${\tfrac {1}{3}}$ площади единичного квадрата. Отсюда следует, что сумма приведенного выше ряда равна ${\tfrac {4}{3}}$ (с $1+{\tfrac {1}{3}}={\tfrac {4}{3}}$).

См. также

• Квадратура (геометрия)
• История исчисления

Дальнейшее чтение

• Ахосе, Сандей и Роджер Нельсен (июнь 1994 г.). «Доказательство без слов: геометрический ряд». Журнал «Математика» . 67 (3): 230. дои : 10.2307/2690617 . JSTOR   2690617 .
• Анкора, Лучано (2014). «Квадратура параболы с квадратным пирамидальным числом» . Архимед . 66 (3).
• Брессуд, Дэвид М. (2006). Радикальный подход к реальному анализу (2-е изд.). Математическая ассоциация Америки . ISBN  0-88385-747-2 . .
• Дейкстерхейс, Э.Дж. (1987) «Архимед», Princeton U. Press ISBN   0-691-08421-1
• Эдвардс-младший, Швейцария (1994). Историческое развитие исчисления (3-е изд.). Спрингер. ISBN  0-387-94313-7 . .
• Хит, Томас Л. (2011). Работы Архимеда (2-е изд.). CreateSpace. ISBN  978-1-4637-4473-1 .
• Симмонс, Джордж Ф. (2007). Исчисление драгоценных камней . Математическая ассоциация Америки. ISBN  978-0-88385-561-4 . .
• Штейн, Шерман К. (1999). Архимед: что он делал, кроме крика «Эврика»? . Математическая ассоциация Америки. ISBN  0-88385-718-9 .
• Стиллвелл, Джон (2004). Математика и ее история (2-е изд.). Спрингер. ISBN  0-387-95336-1 . .
• Суэйн, Гордон и Томас Денс (апрель 1998 г.). «Возвращение к квадратуре параболы Архимеда». Журнал «Математика» . 71 (2): 123–30. дои : 10.2307/2691014 . JSTOR   2691014 .
• Уилсон, Алистер Макинтош (1995). Бесконечное в Конечном . Издательство Оксфордского университета . ISBN  0-19-853950-9 . .

Внешние ссылки

• Кассельман, Билл. «Квадратура Архимеда параболы» . Архивировано из оригинала 4 февраля 2012 г. Полный текст в переводе Т.Л. Хита.
• Университета Ксавьера Кафедра математики и информатики . «Архимед Сиракузский» . Архивировано из оригинала 13 января 2016 г. . Текст предложений 1–3 и 20–24 с комментарием.
• http://planetmath.org/ArchimedesCalculus