✖


Jump to content

Древнегреческая астрономия

Эта статья о древнегреческой астрономии. О донаучной космологии в Древней Греции см. Ранняя греческая космология . Чтобы узнать о практике астрономии в древнем Вавилоне, см. Вавилонскую астрономию .
Антикитерский механизм представлял собой аналоговый компьютер 150–100 гг. до н. э., предназначенный для расчета положения астрономических объектов.

Древнегреческая астрономия — это астрономия, написанная на греческом языке во времена классической античности . Под греческой астрономией понимаются древнегреческая , эллинистическая , греко -римская и поздняя античная эпохи. Древнегреческую астрономию можно разделить на три основных этапа: классическую греческую астрономию , которая охватывала V и IV века до нашей эры, и эллинистическую астрономию , которая охватывает последующий период до образования Римской империи ок. 30 г. до н. э., и, наконец, греко-римская астрономия , которая относится к продолжению традиции греческой астрономии в римском мире. В эпоху эллинизма и позже греческая астрономия расширилась за пределы географического региона Греции , поскольку греческий язык стал языком науки во всем эллинистическом мире, в значительной степени ограниченном границами Македонской империи, установленной Александром Великим . Самым выдающимся и влиятельным практиком греческой астрономии был Птолемей , чей трактат «Альмагест» формировал астрономическое мышление вплоть до современной эпохи. Большинство наиболее выдающихся созвездий, известных сегодня, взяты из греческой астрономии, хотя и с использованием терминологии, которую они заимствовали в Латынь . [1]

Греческая астрономия находилась под сильным влиянием вавилонской астрономии и, в меньшей степени, египетской астрономии. астрономами и математиками различных арабо-мусульманских империй средневековья В более поздние периоды древнегреческие астрономические работы переводились и распространялись на других языках, особенно на арабском , . [2]

Ключевые тексты [ править ]

Многие греческие астрономические тексты известны только по названию и, возможно, по описаниям или цитатам. Некоторые элементарные работы сохранились, потому что они не были математическими и подходили для использования в школах. Книги этого класса включают « Явления Евклида » и две работы Автолика Питанского . Три важных учебника, написанных незадолго до времени Птолемея, были написаны Клеомедом , Гемином и Теоном из Смирны . Книги римских авторов, таких как Плиний Старший и Витрувий, содержат некоторую информацию по греческой астрономии. Важнейшим первоисточником является « Альмагест» , поскольку Птолемей ссылается на труды многих своих предшественников. [3]

Начало греческой астрономии [ править ]

космология Ранняя греческая ​

Основная статья: Ранняя греческая космология
Анаксимандр

Основные черты архаической греческой космологии схожи с чертами древней ближневосточной космологии . К ним относятся ( плоская ) земля, небо (твердь), где расположены солнце, луна и звезды, внешний океан, окружающий обитаемое человеческое царство, и преисподняя ( Тартар ), первые три из которых соответствовали богам Урану. , Гея и Океан (или Понтос ). [4] [5] [6]

Ионическая школа [ править ]

Основная статья: Ионическая школа (философия)

Философу Фалесу , одной из главных фигур ионической школы греческой философии, обычно приписывают начало традиции греческой науки . Фалес был первым, кто предложил немифологическое объяснение состава космоса. Как и его предшественники, такие как Гесиод и Гомер , он считал, что Земля была плоской и покоилась на первозданном и бескрайнем океане. Однако он предположил, что Вселенная в основном состоит из воды. [7] Самыми известными продолжателями традиции, начатой ​​Фалесом, были Платон и Аристотель ; хотя многие мысли продолжали полагаться на интуицию, непреходящим наследием этой работы было то, что она предлагала несверхъестественные объяснения нормальному функционированию Вселенной; математика (особенно геометрия ) получила значительное развитие и применялась к решаемым проблемам; и считалось, что наблюдение может дисквалифицировать кандидатов на объяснения того, как устроен мир. [8]

Анаксимандр , ученик Фалеса и еще один видный представитель ионической школы, понял, что северное небо словно вращается вокруг Полярной звезды , что привело его к представлению о Небесной сфере вокруг Земли. И поскольку небо, похоже, меняется в зависимости от широты, он также считал, что поверхность Земли также может быть искривленной. Однако он ошибочно полагал, что Земля представляет собой цилиндр, а не сферу. Идея о сферической Земле впервые нашла аудиторию у пифагорейцев , но это было связано с философскими, а не с научными причинами: сфера считалась идеально геометрической фигурой. [9]

Фреймворк [ править ]

Аксиомы [ править ]

Согласно Птолемею в его «Альмагесте» (1.2), греческая астрономия основывалась на следующих предположениях (или гипотезах в греческой терминологии): [10]

  • Небеса имеют сферическую форму
  • Небесная сфера вращается
  • Земля имеет сферическую форму
  • Земля – центр космоса
  • «Земля по размеру и расстоянию имеет отношение точки к сфере неподвижных звезд»
  • Земля неподвижна

В первую книгу «Альмагеста» вошла глава, посвященная защите каждого из этих предположений и опровержению альтернативных позиций с использованием как философии, так и астрономических наблюдений. [11]

Планеты [ править ]

Основная статья: Классическая планета

Термин «планета» происходит от греческого термина πλανήτης ( planetēs ), что означает «странник», поскольку древние астрономы отмечали, как определенные точки света перемещались по небу относительно других звезд (которые кажутся неподвижными). Пять планет можно увидеть невооруженным глазом: Меркурий , Венера , Марс , Юпитер и Сатурн ; их греческие имена — Гермес, Афродита, Арес, Зевс и Кронос. [12] Ранние греческие астрономы считали, что вечернее и утреннее появление Венеры представляют собой два разных объекта, называя ее Геспер («вечерняя звезда»), когда она появлялась на вечернем западном небе, и Фосфор («несущий свет»), когда она появлялась утром на востоке. небо. В конце концов они пришли к выводу, что оба объекта представляют собой одну и ту же планету. по-разному приписывают Пифагору или Пармениду . За это открытие [13]

Созвездия [ править ]

Обычно считается, что Евдокс стандартизировал названия созвездий. Самое раннее из дошедших до нас описаний созвездий, « Явления Арата » (270 г. до н.э.), является основным источником его работ по этой теме. Седьмая и восьмая книги Альмагеста составят звездный каталог названий, положений и величин более тысячи звезд, которые Птолемей поместил в традиционную классификацию 48 созвездий. Самыми важными из них были двенадцать созвездий, определявших зодиак . [14]

Размеры астральных тел [ править ]

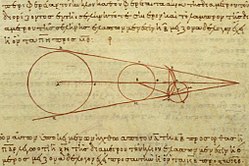
Аристарх также написал книгу «О размерах и расстояниях Солнца и Луны» , которая является его единственной сохранившейся работой. В этой работе он рассчитал размеры Солнца и Луны, а также их расстояния от Земли в земных радиусах . Вскоре после этого Эратосфен рассчитал размер Земли, указав значение радиуса Земли в 252 000 стадий , что может быть эквивалентно 39 690 километрам, что довольно близко к истинной цифре в 40 120 километров. [15] Гиппарх написал еще одну книгу «О размерах и расстояниях Солнца и Луны» , которая не сохранилась. И Аристарх, и Гиппарх резко недооценили расстояние Солнца от Земли. [16]

Геоцентризм и гелиоцентризм [ править ]

Расчеты Аристарха в III веке до нашей эры относительно относительных размеров (слева направо) Солнца, Земли и Луны из греческой копии X века нашей эры.

Геоцентризм , идея о том, что Земля находится в центре Солнечной системы (или даже космоса) и что другие небесные тела, включая Солнце, Луну и планеты, вращаются вокруг нее, была доминирующей в Древней Греции и древних космографических системах. в целом. Однако в то или иное время появлялись различные альтернативы. Например, пифагорейская астрономическая система , предложенная Филолаем в V веке до нашей эры, предполагала существование невидимого «Центрального огня» (не путать с Солнцем), вокруг которого вращались все остальные тела космоса. [17] Гераклид Понтийский постулировал геогелиоцентрическую систему, в которой Солнце вращалось вокруг Земли, но все остальные тела вращались вокруг Солнца. [18] Наконец, в III веке до нашей эры Аристарх Самосский (иногда называемый «Древним Коперником ») [19] ) был первым и единственным деятелем досовременного периода, предложившим поистине гелиоцентрическую модель Солнечной системы , поместившую в центр Вселенной Солнце, а не Землю. [20]

Классическая греческая астрономия [ править ]

Платон и Евдокс Книдский оба активно занимались астрономической мыслью в первой половине четвертого века до нашей эры, и вместе с ними произошел решающий сдвиг в греческой астрономии. Работа этих двух деятелей представляет собой переход от прежних звездных забот, сосредоточенных на изучении звезд, к изучению планет. Была предложена новая двухсферная модель Солнечной системы, и впервые объяснения планетных наблюдений были даны в форме геометрических теорий. [21] Модель двух сфер утверждает, что небо и земля представляют собой пару концентрических сфер. То есть и небо, и земля представляются сферой, имеющей один и тот же центр. [21] Таким образом, они напоминают структуру (концептуально сферического) яйца, в котором внешняя сфера (небо) охватывает внутреннюю сферу (землю). [22] Внешняя небесная сфера содержит неподвижные звезды, а также Солнце, Луну и планеты, движущиеся по ее поверхности. Внутренняя земная сфера зафиксирована в центре. Из этого возникает концепция « небесного экватора », который аналогичен экватору Земли, проецированному наружу на небесную сферу. Термин « эклиптика » относится к годовому пути Солнца вокруг небесной сферы. Эта траектория наклонена на 23° относительно небесного экватора. Два места, где встречаются эклиптика и небесный экватор, представляют собой точки равноденствия (весной и осенью ) . Две точки, где эклиптика находится дальше всего от экватора, представляют дни солнцестояния ( летнего и зимнего ). [23]

Гравюра на дереве эпохи Возрождения, иллюстрирующая модель двух сфер.

Евдокс Книдский жил и занимался астрономией в первой половине четвертого века до нашей эры. Его труды утеряны, поэтому сведения о нем поступают из второстепенных упоминаний в древних текстах. Существует группа фрагментов об астрономии четвертого века до нашей эры, известная как Папирус Евдокса , но она содержит мало важной информации о взглядах самого Евдокса. [24] Согласно Гиппарху в его комментарии к «Арату» , Евдокс, как полагают, написал, что одно из них называется «Зеркало» , а другое — «Феномены» , хотя Октаэтерис . ему под псевдонимом приписывают [25] Другая работа, «О скоростях» , попыталась понять тогдашние непредсказуемые движения планет. [26] Он начал свою работу в Афинах и Египте , а затем основал школу в Кизике , где приобрел свою репутацию. Среди его учеников Менайхмос , известный как изобретатель понятия конических сечений, и Полемарх, чей ученик Каллипп предложил хорошо принятые модификации евдоксановой теории гомоцентрических сфер. Он также внес свой вклад в создание календаря и литературы о парапегме . [25]

Сохранилась модель движения планет Евдокса, резюмированная Аристотелем ( «Метафизика» XII, 8), а также комментарий Симплиция к De caelo Аристотеля, созданный в VI веке нашей эры. [27] Модель Евдокса попыталась объяснить наблюдаемые движения планет. Ключевым способом, с помощью которого это было сделано, было утверждение, что неподвижные звезды перемещались по одной вращающейся сфере, тогда как каждая из планет двигалась по нескольким вложенным вращающимся сферам, каждая со своей собственной скоростью и полюсом. Евдокс основал школу мысли, которая отдавала предпочтение использованию геометрических моделей для объяснения видимых путей звезд. [26] Некоторые, однако, заметили недостатки в системе Евдокса. Автолик из Питаны заметил, что луна будет иметь разный размер, если наблюдения будут проводиться в разное время. Однако это противоречило теории гомоцентриков Евдоксана, поскольку она не допускала какого-либо изменения расстояния между Землей и Луной. [28]

Эллинистическая астрономия [ править ]

Аполлоний Пергский [ править ]

Основная статья: Аполлоний Пергский

Аполлоний Пергский ( ок. 240 г. до н. э. – ок. 190 г. до н. э. ) отреагировал на проблемы более ранних астрономических теорий, особенно теории Евдокса, создав теорию эксцентриков и эпициклов (и их производных). Это было далее развито Гиппархом во втором веке до нашей эры, а затем Птолемеем во втором веке нашей эры. Эта модель позволила теории объяснить изменения расстояния между Землей и другими астральными телами. [28] Однако, хотя Аполлонию часто приписывают разработку этой теории, некоторые считают, что доказательства этого недостаточны. Некоторые свидетельства могут быть связаны с более ранним автором, Архимедом , со знанием эпициклов и эксцентриков, а механизм Антикитеры также, по-видимому, предполагает эксцентрики и эпициклы в способе выполнения вычислений. [29]

Гиппарх [ править ]

Основная статья: Гиппарх

Гиппарх был важной фигурой греческой астрономии во II веке до нашей эры. Он составил звездный каталог , по словам Плиния Старшего наблюдал новую (новую звезду) и обнаружил прецессию равноденствий . Похоже, он располагал существенной информацией о вавилонских астрономах ; У предыдущих греческих авторов не существует никаких указаний на такое знание вавилонской астрономии. [30] Неизвестно, как он получил доступ к этой информации. [31] и вполне вероятно, что знания вавилонской астрономии среди преемников Гиппарха в более поздние эпохи, таких как Птолемей, полагались на Гиппарха в качестве информации о ней. [32] Наблюдения Гиппарха позволили ему обнаружить, что тропический год длится чуть меньше 365,25 дней, тогда как сидерический год чуть больше 365,25 дней. Теперь известно, что Гиппарх был прав, хотя неясно, как Гиппарх это обнаружил. [33]

Птолемеева астрономия [ править ]

Основная статья: астрономия Птолемея

Обзор [ править ]

Клавдий Птолемей был математиком, который работал в городе Александрия в Римском Египте во 2 веке нашей эры, глубоко исследуя форму и движение Земли и других небесных тел. Самой важной работой Птолемея был « Альмагест» (также известный как « Математическое сочинение» ), и он написал другие произведения, такие как «Гипотезы» , «Тетрабиблос» , «Удобные таблицы» , «Канобическая надпись » и другие второстепенные произведения. [34]

Альмагест ​ [ править ]

Основная статья: Альмагест

«Альмагест » — одна из самых влиятельных книг в истории западной астрономии. «Альмагест » представлял собой монументальную серию из 13 книг, включающую примерно четверть миллиона слов на греческом языке, в которых давалась всесторонняя трактовка астрономии того времени, включающая теоремы, модели и наблюдения многих предшествующих математиков. [35] В 13 книгах рассматриваются следующие темы: [36]

  • Книга 1 объясняет предпосылки и инструменты, с которыми он работает.
  • В книге 2 представлены основные результаты, которых можно достичь с помощью сферической астрономии.
  • В книге 3 представлена ​​теория Солнца.
  • В книге 4 содержится эквивалентное описание Луны.
  • В книге 5 рассматриваются новые сложности, возникающие в результате применения теории Птолемея к Луне, в отличие от более простого случая с Солнцем.
  • Книга 6 объединяет теории Солнца и Луны, создавая теорию, предсказывающую затмения.
  • Книги 7 и 8 начинаются заново; они излагают теорию и практику работы с неподвижными звездами и завершают каталогом из 1022 звезд.
  • Книги с 9 по 13 посвящены пяти видимым (и, следовательно, пяти известным в то время ) планетам.
  • В книге 9 изложен общий подход для всех планет, за которым следует теория Меркурия .
  • Книга 10 посвящена Венере и Марсу .
  • Книга 11 посвящена Юпитеру и Сатурну .
  • Книга 12 посвящена явлениям ретроградации и другим особенностям движения планет.
  • Книга 13 посвящена отклонениям планет от эклиптики.

Эксцентрики и эпициклы [ править ]

Греки стремились объяснить, как модель может объяснить нерегулярное движение небесных тел. Поскольку Луна и другие объекты, по-видимому, меняются в размерах в зависимости от времени наблюдения, предполагалось, что расстояние Земли до других астральных тел меняется и что простое круговое движение другого тела вокруг Земли, как в гомоцентрической теории Евдокса не смог объяснить это. Птолемей принял и развил понятие эксцентриков и эпициклов для объяснения этого явления. Эксцентрик — это положение, согласно которому наблюдатель не находится в центре вращения. Следовательно, если бы Земля не находилась, например, в центре вращения Земли, при наблюдении с Земли казалось бы, что Луна движется неравномерно: когда Луна проходила ближе к Земле, ее движение казалось бы быстрее и больше (потому что было ближе); в противном случае он будет казаться медленнее и меньше. Идея эпицикла заключалась в том, чтобы сказать, что вокруг Земли существует круг вращения, но отвергнуть идею о том, что само вращающееся тело будет помещено в этот круг. Вместо этого меньший вращающийся круг будет помещен в больший круг, вращающийся вокруг Земли, и этот меньший круг называется деферентом. При движении тела вращается вокруг окружности деферента, в то время как сам деферент будет вращаться вокруг земли. Это также позволило бы наблюдателю с Земли наблюдать неравномерное движение астрального тела. [37]

Эксцентрики и эпициклы — два основных инструмента птолемеевской астрономии, и Птолемей продемонстрировал, что они тесно связаны. В случае с Солнцем Птолемей понимал, что его движение можно предсказать либо по эксцентрику, либо по эпициклу. [38] Когда в модель были добавлены небесные тела, отличные от Солнца, например планеты, она стала более сложной. Модели Юпитера, Сатурна и Марса включали центр круга, точку экванты, эпицикл и наблюдателя с Земли для определения перспективы. Открытие этой модели заключалось в том, что центр эпициклов Меркурия и Венеры всегда должен быть коллинеарен Солнцу. Это обеспечивает ограниченное удлинение. [39] Ограниченная элонгация — это угловое расстояние небесных тел от центра Вселенной. Птолемея Модель космоса и его исследования обеспечили ему важное место в истории в развитии современной науки. В системе Птолемея Земля находилась в центре Вселенной, а вокруг нее вращались Луна, Солнце и пять планет. Круг неподвижных звезд обозначал самую внешнюю сферу Вселенной, а за ней должно было находиться философское царство «эфира». Земля находилась в точном центре космоса. Сфера, несущая Луну, описывается как граница между тленным и изменчивым подлунным миром и нетленным и неизменным небом над ним. [40]

Влияние [ править ]

Птолемея Альмагеста Получение ​ ​

Астрономия Птолемея стала стандартом в средневековой западноевропейской и исламской астрономии ее не вытеснили Мараганская , гелиоцентрическая и Тихоническая системы , пока к 16 веку .

Первое критическое обсуждение Альмагеста было сделано Артемидором в конце второго или начале третьего века, хотя он плохо его понимал. В четвертом веке Папп Александрийский и Теон Александрийский составили комментарии или трактаты к разделам Альмагеста. [41] Однако эти работы были направлены только на понимание Альмагеста, а не на его улучшение или развитие. Ситуация изменилась в пятом веке с появлением неоплатоника философа- Прокла . Его изложение «Альмагеста», в отличие от его предшественников, продемонстрировало детальное понимание технических деталей работы Птолемея. Хотя Прокл критиковал некоторые элементы Альмагеста, такие как предположение о существовании эпициклов, он и будущие неоплатоники полагали, что астрономия важна для теологии, и продолжали читать работы Птолемея. Среди учеников и преемников Прокла, продолживших работу в традиции Альмагеста, были Иларий Антиохийский и Марин. Плохо изученный полномасштабный комментарий к «Альмагесту» был создан в шестом веке, и для историков представляет интерес значительное количество схолий на его полях и между колонками, написанных писцами, копирующими текст в более поздние века, которые в дальнейшем связаны с «Альмагестом». Однако автор оригинального комментария неизвестен, поскольку в эту эпоху жило много вероятных кандидатов, изучавших астрономию Птолемея, например, Евтокий Аскалонский и Иоанн Филопон . [42]

Индийская астрономия [ править ]

Дополнительная информация: индийская астрономия.
Греческие экваториальные солнечные часы , Ай-Ханум , Афганистан, III-II века до нашей эры.

Известно также, что несколько греко-римских астрологических трактатов были импортированы в Индию в течение первых нескольких столетий нашей эры. Яванаджатака сатрапов («Изречения греков») была переведена с греческого на санскрит Яванешварой во II веке под патронажем западных саков короля Рудрадамана I. Столица Рудрадамана Удджайн «стала Гринвичем индийских астрономов и Арином арабских и латинских астрономических трактатов; поскольку именно он и его преемники способствовали внедрению греческой гороскопии и астрономии в Индию». [43]

Позже, в VI веке, Ромака Сиддханта («Учение римлян») и Паулиса Сиддханта (иногда называемая «Доктриной Павла » или вообще Доктриной Паулиса Муни) считались двумя из пяти основных астрологических учений. трактаты, которые были составлены Варахамихирой в его Панча-сиддхантике («Пять трактатов»). [44]

греческие Известные астрономы ​

Помимо названных в статье авторов, может представлять интерес следующий список людей, занимавшихся математической астрономией или космологией.

См. также [ править ]

Ссылки [ править ]

Цитаты [ править ]

  1. ^ Терстон 2012 , с. 2.
  2. ^ Пингри 1973 .
  3. ^ Эванс 1998 , с. 24.
  4. ^ Клэй 1992 , с. 132.
  5. ^ Маринатос 2010 , с. 196
  6. ^ Саймон-Шошан 2008 , с. 70–71.
  7. ^ Беннетт и др. 2017 , стр. 16.
  8. ^ Беннетт и др. 2017 , стр. 16–17.
  9. ^ Беннетт и др. 2017 , стр. 17.
  10. ^ Монтель 2020 , с. 9.
  11. ^ Монтель 2020 , с. 9–10.
  12. ^ Эванс 2022 , с. 1–7.
  13. ^ Росс 2020 , с. 163.
  14. ^ Монтель 2020 , с. 11.
  15. ^ Кладжетт 1955 , с. 92–93.
  16. ^ Нойгебауэр 1975 , с. 325-327.
  17. ^ Гросу 2019 , стр. 54.
  18. ^ Гросу 2019 , стр. 57.
  19. ^ Хит 1913 .
  20. ^ Гросу 2019 , стр. 57–58.
  21. ^ Jump up to: Перейти обратно: а б Линдберг 2010 , с. 86.
  22. ^ Бэйли 1943 , с. 135–136.
  23. ^ Линдберг 2010 , с. 86–87.
  24. ^ Нойгебауэр 1975 , с. 675-676.
  25. ^ Jump up to: Перейти обратно: а б Нойгебауэр 1975 , с. 676.
  26. ^ Jump up to: Перейти обратно: а б Чистый 2022 , с. 85.
  27. ^ Нойгебауэр 1975 , с. 677.
  28. ^ Jump up to: Перейти обратно: а б Вильдберг 1988 , с. 122.
  29. ^ Чистый 2022 , с. 319-322.
  30. ^ Чистый 2022 , с. 324.
  31. ^ Чистый 2022 , с. 327.
  32. ^ Чистый 2022 , с. 329.
  33. ^ Чистый 2022 , с. 328-329.
  34. ^ Чистый 2022 , с. 360-366.
  35. ^ Чистый 2022 , с. 366.
  36. ^ Чистый 2022 , с. 366-368.
  37. ^ Чистый 2022 , с. 318-319.
  38. ^ Чистый 2022 , с. 319.
  39. ^ Боулер и Морус 2010 , с. 48.
  40. ^ Боулер и Морус 2010 , с. 26.
  41. ^ Пингри 1994 , с. 75–78.
  42. ^ Пингри 1994 , с. 78–95.
  43. ^ Пингри 1963 .
  44. ^ Гилберт 2024 .

Источники [ править ]

Дальнейшее чтение [ править ]

Внешние ссылки [ править ]

Викискладе есть медиафайлы, связанные с древнегреческой астрономией .
Retrieved from "https://en.wikipedia.org/w/index.php?title=Ancient_Greek_astronomy&oldid=1226383897"
Arc.Ask3.Ru: конец переведенного документа.
Arc.Ask3.Ru
Номер скриншота №: 2ada540fcd6b088294cbe4525c89ca2f__1717047480
URL1:https://arc.ask3.ru/arc/aa/2a/2f/2ada540fcd6b088294cbe4525c89ca2f.html
Заголовок, (Title) документа по адресу, URL1:
Ancient Greek astronomy - Wikipedia
Данный printscreen веб страницы (снимок веб страницы, скриншот веб страницы), визуально-программная копия документа расположенного по адресу URL1 и сохраненная в файл, имеет: квалифицированную, усовершенствованную (подтверждены: метки времени, валидность сертификата), открепленную ЭЦП (приложена к данному файлу), что может быть использовано для подтверждения содержания и факта существования документа в этот момент времени. Права на данный скриншот принадлежат администрации Ask3.ru, использование в качестве доказательства только с письменного разрешения правообладателя скриншота. Администрация Ask3.ru не несет ответственности за информацию размещенную на данном скриншоте. Права на прочие зарегистрированные элементы любого права, изображенные на снимках принадлежат их владельцам. Качество перевода предоставляется как есть. Любые претензии, иски не могут быть предъявлены. Если вы не согласны с любым пунктом перечисленным выше, вы не можете использовать данный сайт и информация размещенную на нем (сайте/странице), немедленно покиньте данный сайт. В случае нарушения любого пункта перечисленного выше, штраф 55! (Пятьдесят пять факториал, Денежную единицу (имеющую самостоятельную стоимость) можете выбрать самостоятельно, выплаичвается товарами в течение 7 дней с момента нарушения.)