Луна (геометрия)



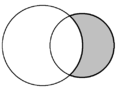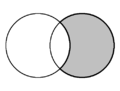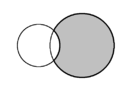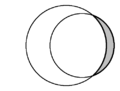
В плоской геометрии форма полумесяца , образованная двумя пересекающимися кругами, называется луной . На каждой диаграмме присутствуют две луны, одна из которых закрашена серым цветом.

В плоской геометрии луна luna (от лат. « луна») — вогнуто-выпуклая область, ограниченная двумя дугами окружностей . ^[1] Он имеет один граничный участок, для которого соединительный отрезок любых двух соседних точек выходит за пределы области, и другой граничный участок, для которого соединительный отрезок любых двух соседних точек полностью лежит внутри области. Выпуклая-выпуклая область называется линзой . ^[2]

Формально луна — это относительное дополнение одного диска к другому (где они пересекаются, но ни один из них не является подмножеством другого). Альтернативно, если $A$ и $B$ это диски, то $A\smallsetminus A\cap B$ это луна.

Квадратура луны [ править ]

В V веке до нашей эры Гиппократ Хиосский показал, что Луну Гиппократа и две другие луны можно точно возвести в квадрат (преобразовать в квадрат, имеющий ту же площадь) с помощью линейки и циркуля . В 1766 году финский математик Даниэль Вейнквист, цитируя Даниэля Бернулли , перечислил все пять геометрических квадратных лун, добавив к тем, которые были известны Гиппократу. В 1771 году Леонард Эйлер предложил общий подход и получил определенное уравнение к проблеме. и его ученик Анатолий Дороднов доказали В 1933 и 1947 годах Николай Чеботарёв , что эти пять лунок являются единственными квадратурируемыми лунами. ^[3]^[1]

Площадь [ править ]

Площадь луны, образованной кругами радиусов a и b ( b>a ) с расстоянием c между их центрами, равна ^[3]

A=2\Delta +a^{2}\sec ^{-1}\left({\frac {2ac}{b^{2}-a^{2}-c^{2}}}\right)-b^{2}\sec ^{-1}\left({\frac {2bc}{b^{2}+c^{2}-a^{2}}}\right),

где ${\text{sec}}^{-1}$ — обратная функция секущей функции , и где

\Delta ={\frac {1}{4}}{\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}

— площадь треугольника со сторонами a, b и c .

См. также [ править ]

Ссылки [ править ]

^ Jump up to: Перейти обратно: ^а ^б История анализа . Х. Н. Янке. Провиденс, Род-Айленд: Американское математическое общество. 2003. с. 17. ISBN 0-8218-2623-9 . OCLC 51607350 . {{cite book}}: CS1 maint: другие ( ссылка )
^ «Группы Google» . Проверено 27 декабря 2015 г.
^ Jump up to: Перейти обратно: ^а ^б Вайсштейн, Эрик В. «Лун» . Математический мир .

Внешние ссылки [ править ]

Пять квадратных лун на MathPages

[Analysis-1] Jump up to: Перейти обратно: ^а ^б История анализа . Х. Н. Янке. Провиденс, Род-Айленд: Американское математическое общество. 2003. с. 17. ISBN 0-8218-2623-9 . OCLC 51607350 . {{cite book}}: CS1 maint: другие ( ссылка )

[2] «Группы Google» . Проверено 27 декабря 2015 г.

[Weisstein-3] Jump up to: Перейти обратно: ^а ^б Вайсштейн, Эрик В. «Лун» . Математический мир .

[1]

[2]

[3]