Арбелос

В геометрии арбелос полукругами — это плоская область, ограниченная тремя с тремя вершинами, причем каждый угол каждого полукруга является общим с одним из других (соединенных), причем все они находятся на одной стороне прямой линии ( базовой линии ), содержащей их диаметры . ^[1]

Самая ранняя известная ссылка на эту фигуру находится в Архимеда » «Книге лемм , где некоторые из ее математических свойств изложены в предложениях с 4 по 8. ^[2] Слово арбелос по-гречески означает «нож сапожника». Фигура тесно связана с цепочкой Паппа .

Характеристики

Два полукруга обязательно вогнутые, с произвольными диаметрами $a$ и $b$ ; третий полукруг выпуклый , диаметром $a + b .$ ^[1]

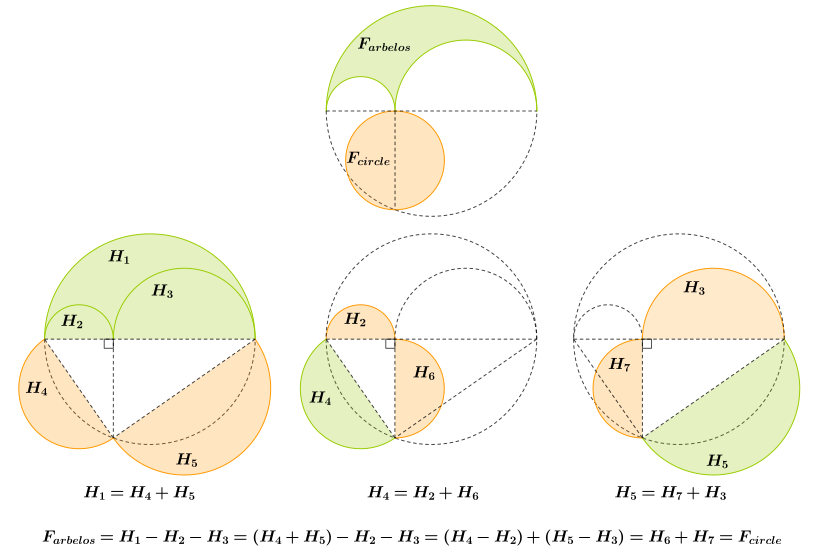
Область

Площадь диаметром арбелоса равна площади круга $HA$ .

Доказательство : Для доказательства отразите арбелы над линией, проходящей через точки $B$ и $C$ , и заметите, что удвоенная площадь арбелов — это то, что останется, если площади двух меньших кругов (диаметрами $BA$ , $AC$ ) вычесть из площадь большого круга (диаметром $BC$ ). Поскольку площадь круга пропорциональна квадрату диаметра ( Евклида » « Начала , книга XII, предложение 2; нам не нужно знать, что константа пропорциональности равна $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ π / 4 ⁠$ ), задача сводится к тому, чтобы показать, что $2|AH|^{2}=|BC|^{2}-|AC|^{2}-|BA|^{2}$ . Длина $| до нашей эры |$ равен сумме длин $| бакалавр |$ и $| переменного тока |$ , поэтому это уравнение алгебраически упрощается до утверждения, что $|AH|^{2}=|BA||AC|$ . Таким образом, утверждается, что длина отрезка $AH$ является средним геометрическим длин отрезков $BA$ и $AC$ . Теперь (см. рисунок) треугольник $BHC$ , будучи вписан в полукруг, имеет прямой угол в точке $Н$ (Евклид, книга III, предложение 31), и, следовательно, $| ХА |$ действительно является «средним пропорциональным» между $| бакалавр |$ и $| переменного тока |$ (Евклид, Книга VI, Положение 8, Поризм). Это доказательство приближается к древнегреческому аргументу; Гарольд П. Боас цитирует статью Роджера Б. Нельсена. ^[3] который реализовал эту идею в качестве следующего доказательства без слов . ^[4]

Прямоугольник

Пусть $D$ и $E$ — точки, в которых отрезки $BH$ и $CH$ пересекают полукруги $AB$ и $AC$ соответственно. Четырехугольник собой $ADHE$ на самом деле представляет прямоугольник .

Доказательство :

∠BDA

,

∠BHC

и

∠AEC

— прямые углы, поскольку они вписаны в полукруги (по теореме Фалеса ). Следовательно, четырехугольник

ADHE

имеет три прямых угла, поэтому он является прямоугольником. КЭД

Касательные

Прямая $DE$ касается полуокружности $BA$ в точке $D$ и полуокружности $AC$ в $E.$ точке

Доказательство : поскольку

∠BDA

— прямой угол,

∠DBA

равно

⁠ π / 2 ⁠

минус

∠DAB

. Однако

∠DAH

также равно

⁠ π / 2 ⁠

минус

∠DAB

(поскольку

∠HAB

— прямой угол). треугольники

DBA

и

DAH

подобны Следовательно , . Следовательно,

∠DIA

равно

∠DOH

, где

I

— середина

BA

, а

O

— середина

AH

. Но

∠AOH

— прямая линия, поэтому

∠DOH

и

∠DOA

— дополнительные углы . Следовательно, сумма

∠DIA

и

∠DOA

равна π.

∠IAO

— прямой угол. Сумма углов в любом четырехугольнике равна 2π, поэтому в четырехугольнике

∠IDO

IDOA

должен

быть прямым углом. Но

ADHE

— прямоугольник, поэтому середина

(

диагонали

O AH

прямоугольника) также является серединой

DE

(другой диагонали прямоугольника). Поскольку

I

(определяемый как середина

BA

) является центром полукруга

BA

, а угол

∠IDE

является прямым углом, то

DE

касается полукруга

BA

в точке

D

. По аналогичным рассуждениям

DE

касается полукруга

AC

в

E.

точке КЭД

круги Архимеда

Высота $AH$ делит арбелос на две области, каждая из которых ограничена полукругом, отрезком прямой и дугой внешнего полукруга. Круги, вписанные в каждую из этих областей, известные как архимедовы круги арбелов, имеют одинаковый размер.

Вариации и обобщения

Парбелос — это фигура, похожая на арбелос, в которой параболы вместо полукругов используются сегменты . Обобщением, включающим как арбелос, так и парбелос, является f -белос, в котором используется определенный тип подобных дифференцируемых функций. ^[5]

В полуплоской модели Пуанкаре гиперболической плоскости арбелос моделирует идеальный треугольник .

Этимология

Название арбелос происходит от греческого ἡ ἄρβηλος he árbelos или ἄρβυλος árbylos , что означает «нож сапожника», нож, используемый сапожниками с древности до наших дней, лезвие которого, как говорят, напоминает геометрическую фигуру.

См. также

Ссылки

^ Jump up to: Перейти обратно: ^а ^б Вайсштейн, Эрик В. «Арбелос» . Математический мир .
^ Томас Литтл Хит (1897), Работы Архимеда . Издательство Кембриджского университета. Предложение 4 в книге лемм . Цитата: Если AB — диаметр полукруга, а N — любая точка на AB, и если полукруги описываются внутри первого полукруга и имеют диаметры AN, BN соответственно, то фигура, заключенная между окружностями трех полукругов, — это «то, что Архимед назвал арбелос"; а его площадь равна диаметру круга на ПН, где ПН перпендикулярна АВ и встречается с исходным полукругом на П. ( "Арбелос - Нож сапожника" )
^ Нельсен, РБ (2002). «Доказательство без слов: Площадь арбелоса». Математика. Маг . 75 (2): 144. дои : 10.2307/3219152 . JSTOR 3219152 .
^ Боас, Гарольд П. (2006). «Размышления об Арбелосах» . Американский математический ежемесячник . 113 (3): 236–249. дои : 10.2307/27641891 . JSTOR 27641891 .
^ Антонио М. Оллер-Марсен: «Ф-белос» . В: Геометрический форум , Том 13 (2013), стр. 103–111.

Библиография

Джонсон, РА (1960). Продвинутая евклидова геометрия: элементарный трактат по геометрии треугольника и круга (перепечатка издания 1929 года под ред. Хоутона Миффлина). Нью-Йорк: Dover Publications. стр. 116–117. ISBN 978-0-486-46237-0 .
Огилви, CS (1990). Экскурсии по геометрии . Дувр. стр. 51–54 . ISBN 0-486-26530-7 .
Сондоу, Дж. (2013). «Парбелос, параболический аналог арбелоса». амер. Математика. Ежемесячно . 120 (10): 929–935. arXiv : 1210.2279 . doi : 10.4169/amer.math.monthly.120.10.929 . S2CID 33402874 . American Mathematical Monthly , 120 (2013), 929–935.
Уэллс, Д. (1991). Словарь любопытной и интересной геометрии Penguin . Нью-Йорк: Книги Пингвина. стр. 5–6 . ISBN 0-14-011813-6 .

Внешние ссылки

СМИ, связанные с Арбелосом, на Викискладе?
Словарное определение арбелоса в Викисловаре

[wolfram-1] Jump up to: Перейти обратно: ^а ^б Вайсштейн, Эрик В. «Арбелос» . Математический мир .

[archBLprop4-2] Томас Литтл Хит (1897), Работы Архимеда . Издательство Кембриджского университета. Предложение 4 в книге лемм . Цитата: Если AB — диаметр полукруга, а N — любая точка на AB, и если полукруги описываются внутри первого полукруга и имеют диаметры AN, BN соответственно, то фигура, заключенная между окружностями трех полукругов, — это «то, что Архимед назвал арбелос"; а его площадь равна диаметру круга на ПН, где ПН перпендикулярна АВ и встречается с исходным полукругом на П. ( "Арбелос - Нож сапожника" )

[RBNelsen_2002-3] Нельсен, РБ (2002). «Доказательство без слов: Площадь арбелоса». Математика. Маг . 75 (2): 144. дои : 10.2307/3219152 . JSTOR 3219152 .

[4] Боас, Гарольд П. (2006). «Размышления об Арбелосах» . Американский математический ежемесячник . 113 (3): 236–249. дои : 10.2307/27641891 . JSTOR 27641891 .

[5] Антонио М. Оллер-Марсен: «Ф-белос» . В: Геометрический форум , Том 13 (2013), стр. 103–111.

[1]

[2]

[3]

[4]

[5]