Наклонить линии

В трехмерной геометрии косые линии — это две линии , которые не пересекаются и не параллельны . Простым примером пары перекосов является пара линий, проходящих через противоположные ребра правильного тетраэдра . Две линии, лежащие в одной плоскости, должны либо пересекать друг друга, либо быть параллельными, поэтому скошенные линии могут существовать только в трех или более измерениях . Две прямые перекошены тогда и только тогда, когда они не компланарны .

Общее положение [ править ]

Если четыре точки выбраны случайным образом равномерно внутри единичного куба , они почти наверняка будут определять пару наклонных линий. После выбора первых трех точек четвертая точка будет определять неперекосную линию тогда и только тогда, когда она компланарна первым трем точкам. Однако плоскость, проходящая через первые три точки, образует подмножество нулевой меры куба, и вероятность того, что четвертая точка лежит на этой плоскости, равна нулю. В противном случае линии, определяемые точками, будут перекошены.

Точно так же в трехмерном пространстве очень небольшое возмущение любых двух параллельных или пересекающихся линий почти наверняка превратит их в косые. Поэтому любые четыре точки общего положения всегда образуют косые линии.

В этом смысле перекосы являются «обычным» случаем, а параллельные или пересекающиеся линии — особыми случаями.

Formulas[editФормулы

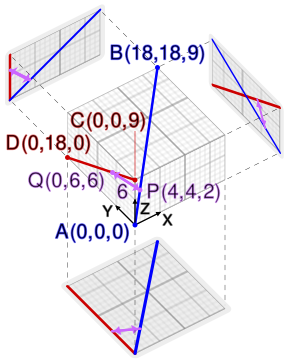
Тестирование на асимметрию [ править ]

Если каждая линия в паре наклонных линий определяется двумя точками через которые она проходит, то эти четыре точки не должны быть компланарными, поэтому они должны быть вершинами тетраэдра , ненулевого объема . И наоборот, любые две пары точек, определяющие тетраэдр ненулевого объема, также определяют пару наклонных линий. Следовательно, проверка того, определяют ли две пары точек наклонные линии, заключается в применении формулы объема тетраэдра через его четыре вершины. Обозначая одну точку как вектор $a$ 1×3 , три элемента которого являются тремя значениями координат точки, и аналогичным образом обозначая $b$ , $c$ и $d$ для других точек, мы можем проверить, не перекошена ли линия, проходящая через $a$ и $b$ , к линии, проходящей через $c$ и $d$ , проверив, дает ли формула объема тетраэдра ненулевой результат:

V={\frac {1}{6}}\left|\det \left[{\begin{matrix}\mathbf {a} -\mathbf {b} \\\mathbf {b} -\mathbf {c} \\\mathbf {c} -\mathbf {d} \end{matrix}}\right]\right|.

Ближайшие точки [ править ]

Выражение двух линий как векторов:

{\text{Line 1:}}\;\mathbf {v_{1}} =\mathbf {p_{1}} +t_{1}\mathbf {d_{1}}

{\text{Line 2:}}\;\mathbf {v_{2}} =\mathbf {p_{2}} +t_{2}\mathbf {d_{2}}

Перекрестное произведение $\mathbf {d_{1}}$ и $\mathbf {d_{2}}$ перпендикулярен прямым.

\mathbf {n} =\mathbf {d_{1}} \times \mathbf {d_{2}}

Плоскость, образованная сдвигами Линии 2 вдоль $\mathbf {n}$ содержит точку $\mathbf {p_{2}}$ и перпендикулярен $\mathbf {n_{2}} =\mathbf {d_{2}} \times \mathbf {n}$ .

Следовательно, точка пересечения линии 1 с вышеупомянутой плоскостью, которая также является ближайшей к линии 2 точкой на линии 1, определяется выражением

\mathbf {c_{1}} =\mathbf {p_{1}} +{\frac {(\mathbf {p_{2}} -\mathbf {p_{1}} )\cdot \mathbf {n_{2}} }{\mathbf {d_{1}} \cdot \mathbf {n_{2}} }}\mathbf {d_{1}}

Аналогично, точка на линии 2, ближайшая к линии 1, определяется выражением (где $\mathbf {n_{1}} =\mathbf {d_{1}} \times \mathbf {n}$ )

\mathbf {c_{2}} =\mathbf {p_{2}} +{\frac {(\mathbf {p_{1}} -\mathbf {p_{2}} )\cdot \mathbf {n_{1}} }{\mathbf {d_{2}} \cdot \mathbf {n_{1}} }}\mathbf {d_{2}}

Расстояние [ править ]

Ближайшие точки $\mathbf {c_{1}}$ и $\mathbf {c_{2}}$ образуют кратчайший отрезок линии, соединяющий линию 1 и линию 2:

d=\Vert \mathbf {c_{1}} -\mathbf {c_{2}} \Vert .

Расстояние между ближайшими точками на двух наклонных линиях также можно выразить с помощью других векторов:

\mathbf {x} =\mathbf {a} +\lambda \mathbf {b} ;

\mathbf {y} =\mathbf {c} +\mu \mathbf {d} .

Здесь вектор $x$ 1×3 представляет собой произвольную точку на линии, проходящей через конкретную точку $a$ , где $b$ представляет направление линии и имеет значение действительного числа. $\lambda$ определение того, где находится точка на прямой, и аналогично для произвольной точки $y$ на линии, проходящей через конкретную точку $c$ в направлении $d$ .

Векторное произведение b . и d перпендикулярно прямым, как и единичный вектор

\mathbf {n} ={\frac {\mathbf {b} \times \mathbf {d} }{|\mathbf {b} \times \mathbf {d} |}}

Тогда перпендикулярное расстояние между прямыми будет ^[1]

d=|\mathbf {n} \cdot (\mathbf {c} -\mathbf {a} )|.

(если | b × d | равно нулю, линии параллельны и этот метод использовать нельзя).

Более двух строк [ править ]

Конфигурации [ править ]

Конфигурация . перекосов – это совокупность линий, в которых все пары перекошены Две конфигурации называются изотопными, если можно непрерывно преобразовывать одну конфигурацию в другую, сохраняя на протяжении всего преобразования инвариант, согласно которому все пары линий остаются перекошенными. Любые две конфигурации из двух линий легко увидеть как изотопные, а конфигурации из того же количества линий в измерениях выше трех всегда изотопны, но существует множество неизотопных конфигураций из трех или более линий в трех измерениях. ^[2] Число неизотопных конфигураций из n линий в R ³, начиная с n = 1,

1, 1, 2, 3, 7, 19, 74, ... (последовательность A110887 в OEIS ).

Линейчатые поверхности [ править ]

Если повернуть линию L вокруг другой линии М, наклоненной, но не перпендикулярной ей, поверхность вращения , охваченная L , представляет собой однолистный гиперболоид . видимые на иллюстрации, можно сформировать таким образом, вращая линию L вокруг центральной белой вертикальной линии M. Например, три гиперболоида , Копии L внутри этой поверхности образуют регуляр ; гиперболоид также содержит второе семейство линий, которые также наклонены к M на том же расстоянии, что и L от него, но с противоположным углом, образующим противоположный регуляр. Два правила отображают гиперболоид как линейчатую поверхность .

Аффинное преобразование этой линейчатой поверхности дает поверхность, которая обычно имеет эллиптическое поперечное сечение, а не круглое поперечное сечение, полученное вращением L вокруг L'; такие поверхности также называются однолистными гиперболоидами и снова управляются двумя семействами взаимно скошенных линий. Третий тип линейчатой поверхности — гиперболический параболоид . Как и однолистный гиперболоид, гиперболический параболоид имеет два семейства наклонных линий; в каждом из двух семейств линии параллельны общей плоскости, но не друг другу. Любые три перекоса в R ³ лежат ровно на одной линейчатой поверхности одного из этих типов. ^[3]

Теорема Галлуччи [ править ]

Если все три наклонные линии пересекаются с тремя другими наклонными линиями, любая трансверсия первого набора из трех соответствует любой трансверсали второго набора. ^[4]^[5]

Наклон квартир в более высоких измерениях [ править ]

В многомерном пространстве квартира размерности k называется k -квартирой. Таким образом, линию также можно назвать 1-бемольной.

Обобщая концепцию перекоса линий на d -мерное пространство, i -плоскость и j -плоскость могут быть перекошенными , если $я + j < d$ . Как и в случае с линиями в трехмерном пространстве, косыми плоскостями являются линии, которые не параллельны и не пересекаются.

В аффинном d- пространстве две плоскости любого измерения могут быть параллельными. Однако в проективном пространстве параллелизма не существует; две плоскости должны либо пересекаться, либо быть скошенными. Пусть $I$ — множество точек на i -плоскости, а $J$ — множество точек на j -плоскости. В проективном d -пространстве, если $i + j \geq d$ , то пересечение $I$ и $J$ должно содержать ( i + j − d )-плоскость. ( 0 -бемоль — это точка.)

В любой геометрии, если $I$ и $J$ пересекаются в k -плоскости при $k \geq 0$ , то точки $I \cup J$ определяют ( i + j − k )-плоскость.

См. также [ править ]

Ссылки [ править ]

^ Вайсштейн, Эрик В. , «Расстояние между линиями» , MathWorld
^ Виро, Юлия Дроботухина; Виро, Олег (1990), «Конфигурации косых линий» (PDF) , Ленинградский матем. Ж. (на русском языке), 1 (4): 1027–1050 . Пересмотренная версия на английском языке: arXiv : math.GT/0611374 .
^ Гильберт, Дэвид ; Кон-Воссен, Стефан (1952), Геометрия и воображение (2-е изд.), Челси, стр. 101-116. 13–17, ISBN 0-8284-1087-9
^ Коксетер, HSM (1969), Введение в геометрию (2-е изд.), John Wiley & Sons , стр. 257
^ Г. Галлуччи (1906), «Исследование фигуры восьми линий и ее приложения к геометрии тетраэдра и к теории конфигураций», Доклад Академии физико-математических наук , 3-я серия, 12 : 49–79

Внешние ссылки [ править ]

Вайсштейн, Эрик В. , «Наклонные линии» , MathWorld

[mw-lld-1] Вайсштейн, Эрик В. , «Расстояние между линиями» , MathWorld

[viro-viro-2] Виро, Юлия Дроботухина; Виро, Олег (1990), «Конфигурации косых линий» (PDF) , Ленинградский матем. Ж. (на русском языке), 1 (4): 1027–1050 . Пересмотренная версия на английском языке: arXiv : math.GT/0611374 .

[hilbert-cohn-vossen-3] Гильберт, Дэвид ; Кон-Воссен, Стефан (1952), Геометрия и воображение (2-е изд.), Челси, стр. 101-116. 13–17, ISBN 0-8284-1087-9

[coxeter-4] Коксетер, HSM (1969), Введение в геометрию (2-е изд.), John Wiley & Sons , стр. 257

[galluci-5] Г. Галлуччи (1906), «Исследование фигуры восьми линий и ее приложения к геометрии тетраэдра и к теории конфигураций», Доклад Академии физико-математических наук , 3-я серия, 12 : 49–79

[1]

[2]

[3]

[4]

[5]