Октагон

«Восьмиугольный» перенаправляется сюда. Чтобы узнать о других значениях, см. Октагон (значения) и Октагон (значения) .

Правильный восьмиугольник
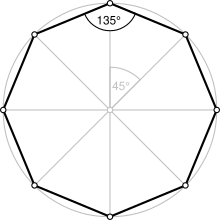Правильный восьмиугольник
Тип	Правильный многоугольник
Ребра и вершины	8
Символ Шлефли	{8}, т{4}
Диаграммы Кокстера – Дынкина
Группа симметрии	Двугранник (Д 8 ), порядка 2х8
Внутренний угол ( градусы )	135°
Характеристики	Выпуклый , циклический , равносторонний , изогональный , изотоксальный
Двойной полигон	Себя

В геометрии восьмиугольник октагонон (от древнегреческого ὀκτάγωνον ( «восемь углов ) ») представляет собой восьмигранный многоугольник или 8-угольник.

Правильный . восьмиугольник имеет символ Шлефли {8} а также может быть построен как квазиправильный усеченный квадрат t{4}, в котором чередуются два типа ребер. Усеченный восьмиугольник t{8} является шестиугольником {16}. Трехмерным аналогом восьмиугольника может быть ромбокубооктаэдр с треугольными гранями на нем как замененными ребрами, если считать восьмиугольник усеченным квадратом.

Характеристики

Диагонали зеленого четырехугольника равны по длине и расположены под прямым углом друг к другу.

Сумма всех внутренних углов любого восьмиугольника равна 1080°. Как и у всех многоугольников, внешние углы составляют 360°.

Если квадраты построены все внутри или все снаружи на сторонах восьмиугольника, то середины отрезков, соединяющих центры противоположных квадратов, образуют четырехугольник, который является одновременно равнодиагональным и ортодиагональным (то есть диагонали которого равны по длине и под прямым углом). углы друг к другу).

Средний восьмиугольник эталонного восьмиугольника имеет восемь вершин в середине сторон эталонного восьмиугольника. Если квадраты построены все внутри или все снаружи на сторонах среднего восьмиугольника, то середины отрезков, соединяющих центры противоположных квадратов, сами образуют вершины квадрата.

Регулярность

Правильный . восьмиугольник — замкнутая фигура со сторонами одинаковой длины и внутренними углами одинакового размера Он имеет восемь линий отражательной симметрии и вращательной симметрии 8-го порядка. Правильный восьмиугольник представлен символом Шлефли {8}.Внутренний угол при каждой вершине правильного восьмиугольника равен 135 ° ( $\scriptstyle {\frac {3\pi }{4}}$ радианы ). Центральный угол равен 45° ( $\scriptstyle {\frac {\pi }{4}}$ радианы).

Область

Площадь правильного восьмиугольника со стороной a определяется выражением

$A=2\cot {\frac {\pi }{8}}a^{2}=2(1+{\sqrt {2}})a^{2}\approx 4.828\,a^{2}.$

С точки зрения радиуса окружности R площадь равна

$A=4\sin {\frac {\pi }{4}}R^{2}=2{\sqrt {2}}R^{2}\approx 2.828\,R^{2}.$

С точки зрения апофемы r (см. также вписанный рисунок ) площадь равна

$A=8\tan {\frac {\pi }{8}}r^{2}=8({\sqrt {2}}-1)r^{2}\approx 3.314\,r^{2}.$

Эти последние два коэффициента заключают в себе значение числа Пи , площади единичного круга .

Площадь можно правильного восьмиугольника вычислить как усеченный квадрат .

Площадь также можно выразить как

$\,\!A=S^{2}-a^{2},$

где S — размах восьмиугольника или вторая по длине диагональ; а — длина одной из сторон или оснований. Это легко доказать, если взять восьмиугольник, нарисовать снаружи квадрат (следя за тем, чтобы четыре из восьми сторон перекрывались с четырьмя сторонами квадрата), а затем взять угловые треугольники (это 45–45–90 треугольников ). и размещает их прямыми углами, направленными внутрь, образуя квадрат. Каждый край этого квадрата равен длине основания.

Учитывая длину стороны a , пролет S равен

$S={\frac {a}{\sqrt {2}}}+a+{\frac {a}{\sqrt {2}}}=(1+{\sqrt {2}})a\approx 2.414a.$

Таким образом, пролет равен соотношению серебра , умноженному на сторону a.

Тогда площадь будет такой же, как указано выше:

$A=((1+{\sqrt {2}})a)^{2}-a^{2}=2(1+{\sqrt {2}})a^{2}\approx 4.828a^{2}.$

Выраженная через пролет площадь равна

$A=2({\sqrt {2}}-1)S^{2}\approx 0.828S^{2}.$

Другая простая формула площади:

$\ A=2aS.$

Чаще известен пролет S длину сторон a и необходимо определить , как при разрезании квадратного куска материала на правильный восьмиугольник. Из вышесказанного,

$a\approx S/2.414.$

Две концевые длины e с каждой стороны (длины сторон треугольников (зеленые на изображении), усеченные из квадрата), а также $e=a/{\sqrt {2}},$ может быть рассчитано как

$\,\!e=(S-a)/2.$

Окружной радиус и внутренний радиус

Радиус описанной окружности правильного восьмиугольника через длину стороны a равен

$R=\left({\frac {\sqrt {4+2{\sqrt {2}}}}{2}}\right)a\approx 1.307a,$

и радиус ​

$r=\left({\frac {1+{\sqrt {2}}}{2}}\right)a\approx 1.207a.$

(то есть половина отношения серебра , умноженная на сторону, a , или половина пролета, S )

Внутренний радиус можно рассчитать по описанному радиусу как

$r=R\cos {\frac {\pi }{8}}$

Диагональность

Правильный восьмиугольник с точки зрения длины стороны a имеет три разных типа диагоналей :

• Короткая диагональ;
• Средняя диагональ (также называемая пролетом или высотой), которая в два раза превышает длину внутреннего радиуса;
• Длинная диагональ, которая в два раза превышает длину описанной окружности.

Формула каждого из них вытекает из основных принципов геометрии. Вот формулы для их длины:

• Короткая диагональ: $a{\sqrt {2+{\sqrt {2}}}}$ ;
• Средняя диагональ: $(1+{\sqrt {2}})a$ ; ( соотношение серебра , умноженное на а)
• Длинная диагональ: $a{\sqrt {4+2{\sqrt {2}}}}$ .

Строительство

построим правильный восьмиугольник, сложив лист бумаги

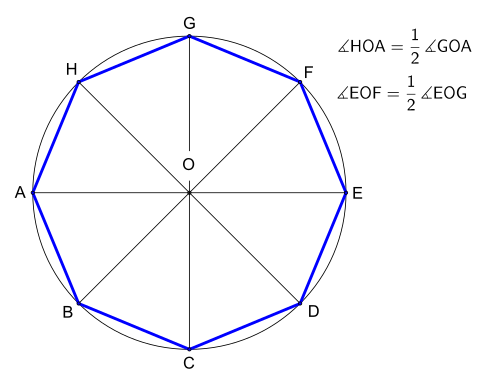
Правильный восьмиугольник по данной описанной окружности можно построить следующим образом:

1. Нарисуйте круг и диаметр AOE, где O — центр, а A, E — точки описанной окружности.
2. Нарисуйте еще один диаметр GOC, перпендикулярный AOE.
3. (Заметим попутно, что A,C,E,G — вершины квадрата).
4. Проведем биссектрисы прямых углов GOA и EOG, составив еще два диаметра HOD и FOB.
5. A,B,C,D,E,F,G,H — вершины восьмиугольника.

Восьмиугольник на заданной описанной окружности

Восьмиугольник с заданной длиной стороны, анимация
(Конструкция очень похожа на конструкцию шестиугольника с заданной длиной стороны .)

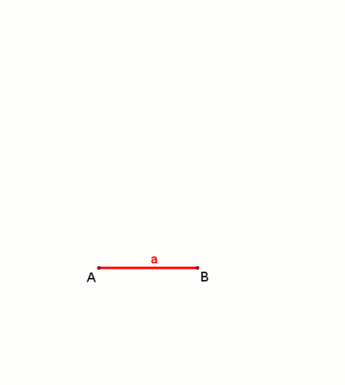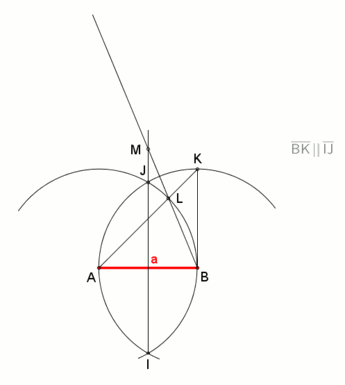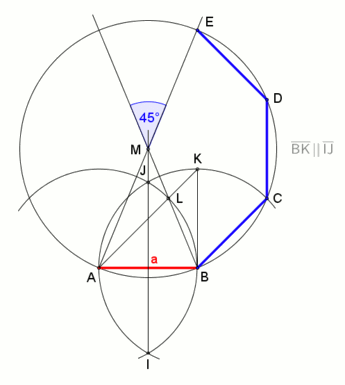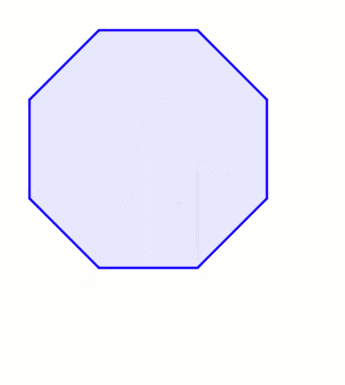
Правильный восьмиугольник можно построить с помощью линейки и циркуля , так как 8 = 2. ³ , степень двойки :

Конструктор восьмиугольной конструкции Meccano.

Правильный восьмиугольник можно построить из брусков конструктора . Требуется двенадцать стержней размера 4, три стержня размера 5 и два стержня размера 6.

Каждая сторона правильного восьмиугольника образует половину прямого угла в центре круга, соединяющего его вершины. Таким образом, его площадь можно вычислить как сумму восьми равнобедренных треугольников, что приводит к следующему результату:

${\text{Area}}=2a^{2}({\sqrt {2}}+1)$

для восьмиугольника со стороной а .

Стандартные координаты

Координаты вершин правильного восьмиугольника с центром в начале координат и длиной стороны 2:

• (±1, ±(1+ √ 2 ))
• (±(1+ √ 2 ), ±1).

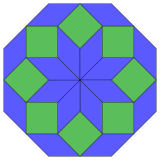
Расчленяемость

8-кубовая проекция	24 ромба рассечение
	Обычный	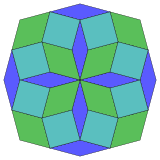изотоксал

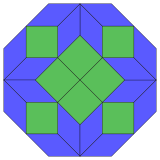Коксетер утверждает, что каждый зоногон (2- метровый угольник, противоположные стороны которого параллельны и одинаковой длины) можно разрезать на m ( m -1)/2 параллелограмма. В частности, это верно для правильных многоугольников с четным числом сторон, и в этом случае все параллелограммы являются ромбами. Для правильного восьмиугольника = 4 m , и его можно разделить на 6 ромбов, один из примеров показан ниже. Это разложение можно рассматривать как 6 из 24 граней в многоугольника Петри плоскости проекции тессеракта . Список (последовательность A006245 в OEIS ) определяет количество решений как восемь по восьми ориентациям этого одного разреза. Эти квадраты и ромбы используются в мозаике Аммана – Бинкера .

Правильный восьмиугольник в разрезе

Тессеракт

4 ромба и 2 квадрата

Перекос

Правильный косой восьмиугольник, рассматриваемый как ребра квадратной антипризмы , симметрия D _4d , [2 ⁺ ,8], (2*4), порядок 16.

Косой восьмиугольник — это косой многоугольник с восемью вершинами и ребрами, но не расположенный в одной плоскости. Внутренняя часть такого восьмиугольника обычно не определена. Косой зигзагообразный восьмиугольник имеет вершины, чередующиеся в двух параллельных плоскостях.

Правильный косой восьмиугольник является вершинно-транзитивным с равными длинами ребер. В трех измерениях это зигзагообразный косой восьмиугольник, который можно увидеть в вершинах и боковых гранях квадратной антипризмы с одинаковым D _4d , [2 ⁺ ,8] симметрия, порядок 16.

Полигоны Петри

Правильный косой восьмиугольник — это многоугольник Петри для этих многомерных правильных и однородных многогранников , показанный в этих косых ортогональных проекциях на _{A 7} , B ₄ и D ₅ плоскости Кокстера .

A 7	Д 5	Б 4
7-симплекс	5-демикуб	16-ячеечный	Тессеракт

Симметрия

Симметрия

Одиннадцать симметрий правильного восьмиугольника. Линии отражений обозначены синим цветом через вершины, фиолетовым через края, а порядок вращения указан в центре. Вершины окрашены в соответствии с их положением симметрии.

Правильный восьмиугольник имеет симметрию Dih ₈ , порядок 16. Есть три подгруппы диэдра: Dih ₄ , Dih ₂ и Dih ₁ , а также четыре циклические подгруппы : Z ₈ , Z ₄ , Z ₂ и Z ₁ , последняя из которых не предполагает симметрии. .

Примеры восьмиугольников по симметрии

р16
d8	g8	стр.8
d4	g4	п4
d2	g2	п2
а1

В правильном восьмиугольнике имеется одиннадцать различных симметрий. Джон Конвей называет полную симметрию r16 . Двугранные симметрии делятся в зависимости от того, проходят ли они через вершины ( d для диагонали) или ребра ( p для перпендикуляров). Циклические симметрии в среднем столбце помечены буквой g для их центрального порядка вращения. Полная симметрия правильной формы — это r16 , а симметрия не помечена как a1 .

Наиболее распространенными восьмиугольниками с высокой симметрией являются p8 , изогональный восьмиугольник, построенный из четырех зеркал, может чередовать длинные и короткие ребра, и d8 , изотоксальный восьмиугольник, построенный с одинаковой длиной ребер, но вершины чередуются с двумя разными внутренними углами. Эти две формы двойственны друг другу и имеют половину порядка симметрии правильного восьмиугольника.

Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только подгруппа g8 не имеет степеней свободы, но ее можно рассматривать как направленные ребра .

Использовать

Восьмиугольный план этажа Купола Скалы , Кудс .

Восьмиугольная форма используется как элемент дизайна в архитектуре. Купол Скалы имеет характерный восьмиугольный план. Башня Ветров в Афинах – еще один пример восьмиугольной конструкции. Восьмиугольный план также использовался в церковной архитектуре , такой как собор Святого Георгия в Аддис-Абебе , базилика Сан-Витале (в Равенне, Италия), Кастель-дель-Монте (Апулия, Италия), флорентийский баптистерий , церковь Цум Фридефюрстен (Германия) и количество восьмиугольных церквей в Норвегии . Центральное пространство Ахенского собора , Каролингская Палатинская капелла , имеет правильный восьмиугольный план. Использование восьмиугольников в церквях также включает в себя меньшие элементы дизайна, такие как восьмиугольная апсида собора Нидарос .

Такие архитекторы, как Джон Эндрюс, использовали восьмиугольную планировку этажей в зданиях для функционального разделения офисных помещений и служб здания, например, в штаб-квартире Intelsat в Вашингтоне или офисах Каллама в Канберре.

• 
  Зонты часто имеют восьмиугольную форму.
• 
  Знаменитый бухарский ковер включает в себя восьмиугольный мотив «слоновья нога».
• 
  Планировка улиц и кварталов Барселоне в района Эшампле основана на неправильных восьмиугольниках.
• 
  Джангги использует восьмиугольные фигуры.
• 
  Японские лотерейные автоматы часто имеют восьмиугольную форму.
• 
  Знак остановки используется в англоязычных странах, а также в большинстве европейских стран.
• 
  Триграммы даосского багуа часто располагаются восьмиугольно.
• 
  Знаменитый восьмиугольный золотой кубок с места кораблекрушения Белитунг.
• 
  Занятия в Шимер-колледже традиционно проходят за восьмиугольными столами.
• 
  Лабиринт Реймсского собора квази-восьмиугольной формы.
• 
  Движение аналоговых джойстиков контроллера Nintendo 64 , контроллера GameCube , Wii Nunchuk и классического контроллера ограничено вращающейся восьмиугольной областью, позволяющей джойстику двигаться только в восьми различных направлениях.
• 
  Стул A la Ronde с восьмиугольными сиденьями и спинками (комплект из восьми штук)

Производные цифры

• 
  Усеченная квадратная мозаика имеет по два восьмиугольника вокруг каждой вершины.
  
• 
  Восьмиугольная призма содержит две восьмиугольные грани.
  
• 
  Восьмиугольная антипризма содержит две восьмиугольные грани.
  
• 
  Усечённый кубооктаэдр содержит 6 восьмиугольных граней.
  
• 
  Всеусеченные кубические соты
  

Связанные многогранники

Восьмиугольник квадрат , как усеченный : стоит первым в последовательности усеченных гиперкубов ,

Усеченные гиперкубы

Изображение								...
Имя	Октагон	Усеченный куб	Усеченный тессеракт	Усеченный 5-куб	Усеченный 6-куб	Усеченный 7-куб	Усеченный 8-куб
Диаграмма Кокстера
Вершинная фигура	( )v( )	( )v{ }	( )v{3}	( )v{3,3}	( )v{3,3,3}	( )v{3,3,3,3}	( )v{3,3,3,3,3}

Как расширенный квадрат, он также является первым в последовательности расширенных гиперкубов:

Расширенные гиперкубы

							...
Октагон	Ромбокубооктаэдр	Сморщенный тессеракт	Стерилизованный 5-куб.	Пятиугольный 6-куб	Шестигранный 7-куб	Гептеллированный 8-куб

См. также

• Бамперный бассейн
• Маленький восьмиугольник Хансена
• Восьмиугольный дом
• Восьмиугольное число
• Октаграмма
• Октаэдр , трехмерная форма с восемью гранями.
• Октогон , крупный перекресток в Будапеште , Венгрия.
• Руб эль-Хизб (также известный как Звезда Аль-Кудс и Звезда Окта)
• Сглаженный восьмиугольник

Внешние ссылки

• Калькулятор восьмиугольников
• Определение и свойства восьмиугольника С интерактивной анимацией