Бесконечный косой многоугольник
Эта статья , возможно, содержит оригинальные исследования . ( декабрь 2019 г. ) |
В геометрии или бесконечный косой многоугольник косой апейрогон — это бесконечный 2- многогранник с вершинами, которые не все являются коллинеарными . Бесконечные зигзагообразные скошенные многоугольники — это двумерные бесконечные скошенные многоугольники с вершинами, чередующимися между двумя параллельными линиями. Бесконечные спиральные многоугольники — это трехмерные бесконечные косые многоугольники с вершинами на поверхности цилиндра .
Правильные бесконечные косые многоугольники существуют в многоугольниках Петри аффинных и гиперболических групп Коксетера . Они построены как единый оператор как композиция всех отражений группы Кокстера.
Правильные зигзагообразные косые апейрогоны в двух измерениях
[ редактировать ]| Правильный зигзагообразный косой апейрогон | |
|---|---|
 | |
| Ребра и вершины | ∞ |
| Символ Шлефли | {∞}#{ } |
| Группа симметрии | D ∞d , [2 + ,∞], (2*∞) |

Правильный зигзагообразный косой апейрогон имеет (2*∞), D ∞d фриза групповую симметрию .
Правильные зигзагообразные косые апейрогоны существуют как многоугольники Петри трех правильных мозаик плоскости: {4,4}, {6,3} и {3,6}. Эти правильные зигзагообразные косые апейрогоны имеют внутренние углы 90 °, 120 ° и 60 ° соответственно от правильных многоугольников внутри мозаики:
 |
Изотоксальные косые апейрогоны в двух измерениях
[ редактировать ]Изотоксальный . апейрогон имеет один тип ребра между двумя чередующимися типами вершин имеет степень свободы Внутренний угол α. {∞ α } — двойственный многоугольник изогональному косому апейрогону.
| {∞ 0° } | |
| {∞ 30° } | 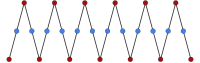 |
Изогональные косые апейрогоны в двух измерениях
[ редактировать ]Изогональные зигзагообразные косые апейрогоны в двух измерениях
[ редактировать ]Изогональный симметрией группы косой апейрогон чередует два типа ребер с различной Фриза . Искаженные правильные зигзагообразные косые апейрогоны образуют изогональные зигзагообразные косые апейрогоны с трансляционной симметрией:
| p1, [∞] + , (∞∞), C ∞ | |
|---|---|
  |   |
Изогональные удлиненные косые апейрогоны в двух измерениях
[ редактировать ]Другие изогональные косые апейрогоны имеют чередующиеся края, параллельные направлению фриза. Эти изогональные вытянутые косые апейрогоны имеют вертикальную зеркальную симметрию в середине ребер, параллельных направлению фриза:
| п2мг, [2 + ,∞], (2*∞), D ∞d | ||
|---|---|---|
 | ||
Квазиправильные удлиненные косые апейрогоны в двух измерениях
[ редактировать ]Изогональный удлиненный косой апейрогон имеет два разных типа ребер; если оба его типа ребер имеют одинаковую длину: его нельзя назвать регулярным, поскольку два его типа ребер все еще различны («транс-ребро» и «цис-ребро»), но его можно назвать квазирегулярным.
Примеры квазиправильных удлиненных косых апейрогонов можно рассматривать как усеченные многоугольники Петри в усеченных правильных мозаиках евклидовой плоскости:
Гиперболические косые апейрогоны
[ редактировать ]Бесконечные правильные косые многоугольники аналогично находятся в евклидовой плоскости и в гиперболической плоскости .
Гиперболические бесконечные правильные косые многоугольники также существуют как многоугольники Петри, зигзагообразные ребра на всех правильных мозаиках гиперболической плоскости . И снова, как и в евклидовой плоскости, гиперболические бесконечные квазиправильные косые многоугольники могут быть построены как усеченные многоугольники Петри внутри ребер всех усеченных правильных мозаик гиперболической плоскости.
| {3,7} | т{3,7} |
|---|---|
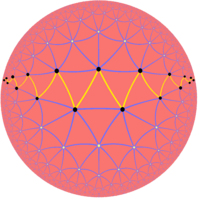 Обычный перекос |  Квазирегулярный перекос |
Бесконечные спиральные многоугольники в трех измерениях
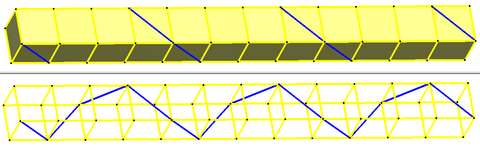
[ редактировать ]{∞} # {3}  Бесконечный правильный винтовой многоугольник (нарисовано в перспективе ) |
Бесконечный спиральный (косой) многоугольник может существовать в трех измерениях, где вершины можно рассматривать как ограниченные поверхностью цилиндра . Эскиз справа представляет собой трехмерное перспективное изображение такого бесконечного правильного спирального многоугольника.
Этот бесконечный спиральный многоугольник можно в основном рассматривать как построенный из вершин бесконечной стопки однородных n -угольных призм или антипризм , хотя в целом угол закручивания не ограничивается целочисленным делителем 180 °. Бесконечный винтовой (косой) многоугольник имеет винтовую симметрию по оси.
Бесконечная стопка призм , например кубов, содержит бесконечный винтовой многоугольник по диагоналям квадратных граней с углом закручивания 90° и с символом Шлефли {∞} # {4}.
Бесконечная стопка антипризм, например октаэдров , образует бесконечные спиральные многоугольники, 3 из которых здесь выделены красным, зеленым и синим цветом, каждый с углом поворота 60° и символом Шлефли {∞} # {6}.
Последовательность ребер спирали Бурдейка – Кокстера может представлять собой бесконечные правильные винтовые многоугольники с иррациональным углом закручивания:
Бесконечные изогональные спиральные многоугольники в трех измерениях
[ редактировать ]Стопка правильных призм может создавать изогональные спиральные апейрогоны с чередующимися краями вокруг оси и вдоль оси; например, стопка кубов может создать изогональный спиральный апейрогон с чередующимися красными и синими краями:
Точно так же чередующаяся стопка призм и антипризм может создать бесконечный изогональный спиральный многоугольник; например, треугольная стопка призм и антипризм с бесконечным изогональным винтовым многоугольником:
Бесконечный изогональный спиральный многоугольник с иррациональным углом закручивания также может быть построен из усеченных тетраэдров, сложенных подобно спирали Бурдейка – Коксетера , с чередованием двух типов ребер между парами шестиугольных граней и парами треугольных граней:
Ссылки
[ редактировать ]- Коксетер , HSM; Правильные комплексные многогранники (1974). Глава 1. Правильные многоугольники , 1.5. Правильные многоугольники в n измерениях, 1.7. Зигзагообразные и антипризматические многоугольники , 1.8. Спиральные многоугольники . 4.3. Флаги и ортосхемы , 11.3. Полигоны Петри