Декагон

Правильный десятиугольник
Правильный десятиугольник
	Правильный десятиугольник
Тип	Правильный многоугольник
Ребра и вершины	10
Символ Шлефли	{10}, т{5}
Диаграммы Кокстера – Динкина	;
Группа симметрии	Двугранник (Д 10 ), заказ 2×10
Внутренний угол ( градусы )	144°
Характеристики	Выпуклый , циклический , равносторонний , изогональный , изотоксальный
Двойной полигон	Себя

В геометрии декагон déka (от греческого δέκα и γωνία gonía, «десять углов») представляет собой десятисторонний многоугольник или 10-угольник. ^[1] Общая сумма внутренних углов простого десятиугольника равна 1440 ° .

Правильный десятиугольник

десятиугольника У правильного все стороны одинаковой длины и каждый внутренний угол всегда равен 144°. ^[1] Его символ Шлефли — {10}. ^[2] а также может быть построен как усеченный пятиугольник t{5}, квазиправильный десятиугольник с чередующимися двумя типами ребер.

Декагоны часто появляются в мозаиках с (частичной) 5-кратной симметрией. На изображениях изображен исламский геометрический узор (15 век), иллюстрация из «Harmonices Mundi» Кеплера (1619 год) и плитка Пенроуза .

Длина стороны

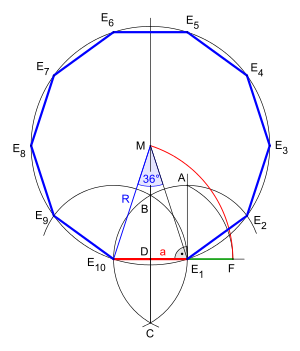
На рисунке изображен правильный десятиугольник с длиной стороны. $a$ и радиус $R$ описанного круга .

Треугольник $E_{10}E_{1}M$ имеет две одинаково длинные ноги длиной $R$ и основание длиной $a$
Круг вокруг $E_{1}$ с радиусом $a$ пересекает $]M\,E_{10}[$ в точку $P$ (на картинке не обозначено).
Теперь треугольник ${E_{10}E_{1}P}\;$ представляет собой равнобедренный треугольник с вершиной $E_{1}$ и с базовыми углами $m\angle E_{1}E_{10}P=m\angle E_{10}PE_{1}=72^{\circ }\;$ .
Поэтому $m\angle PE_{1}E_{10}=180^{\circ }-2\cdot 72^{\circ }=36^{\circ }\;$ . Так $\;m\angle ME_{1}P=72^{\circ }-36^{\circ }=36^{\circ }\;$ и, следовательно, $\;E_{1}MP\;$ также является равнобедренным треугольником с вершиной $P$ . Длина его ног составляет $a$ , поэтому длина $[P\,E_{10}]$ является $R-a$ .
Равнобедренные треугольники $E_{10}E_{1}M\;$ и $PE_{10}E_{1}\;$ имеют равные углы при вершине 36°, поэтому они подобны , следовательно: $\;{\frac {a}{R}}={\frac {R-a}{a}}$
Умножение со знаменателями $R,a>0$ приводит к квадратному уравнению: $\;a^{2}=R^{2}-aR\;$
Это уравнение для длины стороны $a\,$ имеет одно положительное решение: $\;a={\frac {R}{2}}(-1+{\sqrt {5}})$

Таким образом, правильный десятиугольник можно построить с помощью линейки и циркуля .

Дальнейшие выводы

$\;R={\frac {2a}{{\sqrt {5}}-1}}={\frac {a}{2}}({\sqrt {5}}+1)\;$ и базовая высота $\Delta \,E_{10}E_{1}M\,$ (т.е. длина $[M\,D]$ ) является $h={\sqrt {R^{2}-(a/2)^{2}}}={\frac {a}{2}}{\sqrt {5+2{\sqrt {5}}}}\;$ а треугольник имеет площадь: $A_{\Delta }={\frac {a}{2}}\cdot h={\frac {a^{2}}{4}}{\sqrt {5+2{\sqrt {5}}}}$ .

Область

Площадь : правильного десятиугольника со стороной a определяется по формуле ^[3]

A={\frac {5}{2}}a^{2}\cot \left({\frac {\pi }{10}}\right)={\frac {5}{2}}a^{2}{\sqrt {5+2{\sqrt {5}}}}\simeq 7.694208843\,a^{2}

С точки зрения апофемы r (см. также вписанный рисунок ) площадь равна:

A=10\tan \left({\frac {\pi }{10}}\right)r^{2}=2r^{2}{\sqrt {5\left(5-2{\sqrt {5}}\right)}}\simeq 3.249196962\,r^{2}

С точки зрения радиуса окружности R площадь равна:

A=5\sin \left({\frac {\pi }{5}}\right)R^{2}={\frac {5}{2}}R^{2}{\sqrt {\frac {5-{\sqrt {5}}}{2}}}\simeq 2.938926261\,R^{2}

Альтернативная формула: $A=2.5da$ где d — расстояние между параллельными сторонами, или высота, когда одна сторона десятиугольника является основанием, или диаметр вписанной в десятиугольник окружности .По простой тригонометрии ,

d=2a\left(\cos {\tfrac {3\pi }{10}}+\cos {\tfrac {\pi }{10}}\right),

и его можно записать алгебраически как

d=a{\sqrt {5+2{\sqrt {5}}}}.

Строительство

Поскольку 10 = 2 × 5, степень, умноженная на удвоенное простое число Ферма , отсюда следует, что правильный десятиугольник можно построить с помощью циркуля и линейки или путем деления ребра пополам правильного пятиугольника . ^[4]

Строительство декагона

Строительство пятиугольника

Альтернативный (но аналогичный) метод заключается в следующем:

Постройте пятиугольник в круге одним из способов, показанных при построении пятиугольника .
Протяните линию от каждой вершины пятиугольника через центр круга к противоположной стороне того же круга. Там, где каждая линия пересекает круг, является вершиной десятиугольника. Другими словами, изображение правильного пятиугольника при точечном отражении относительно его центра представляет собой концентрический конгруэнтный пятиугольник, а оба пятиугольника в сумме имеют вершины концентрического правильного десятиугольника .
Пять углов пятиугольника составляют альтернативные углы десятиугольника. Соедините эти точки с соседними новыми точками, чтобы сформировать десятиугольник.

Золотое сечение в десятиугольнике

Оба в конструкции с заданной описанной окружностью ^[5] а также при заданной длине стороны является золотым сечением, делящим отрезок на внешнее делениеопределяющий элемент конструкции.

В конструкции с данной описанной окружностью дуга окружности вокруг G радиусом GE ₃ образует отрезок AH , деление которого соответствует золотому сечению.

{\frac {\overline {AM}}{\overline {MH}}}={\frac {\overline {AH}}{\overline {AM}}}={\frac {1+{\sqrt {5}}}{2}}=\Phi \approx 1.618{\text{.}}

В конструкции с заданной длиной стороны ^[6] дуга окружности вокруг D радиусом DA образует отрезок E ₁₀ F , деление которого соответствует золотому сечению .

{\frac {\overline {E_{1}E_{10}}}{\overline {E_{1}F}}}={\frac {\overline {E_{10}F}}{\overline {E_{1}E_{10}}}}={\frac {R}{a}}={\frac {1+{\sqrt {5}}}{2}}=\Phi \approx 1.618{\text{.}}

Десятиугольник с заданной описанной окружностью, ^[5] анимация

Десятиугольник с заданной длиной стороны, ^[6] анимация

Симметрия

Правильный десятиугольник имеет Dih ₁₀ симметрию , порядок 20. Существует 3 симметрии диэдра подгруппы: Dih ₅ , Dih ₂ и Dih ₁ , а также 4 циклической группы симметрии _{: Z 10} , Z ₅ , Z ₂ и Z ₁ .

Эти 8 симметрий можно увидеть в 10 различных симметриях на десятиугольнике, большем количестве, потому что линии отражения могут проходить либо через вершины, либо через ребра. Джон Конвей маркирует их буквенным и групповым порядком. ^[7] Полная симметрия правильной формы — это r20 , а симметрия не помечена как a1 . Двугранные симметрии делятся в зависимости от того, проходят ли они через вершины ( d для диагонали) или ребра ( p для перпендикуляров), и i , когда линии отражения проходят как через ребра, так и через вершины. Циклические симметрии в среднем столбце обозначены буквой g в соответствии с их центральными порядками вращения.

Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только подгруппа g10 не имеет степеней свободы, но ее можно рассматривать как направленные ребра .

Неправильные десятиугольники с наивысшей симметрией - это d10 , изогональный десятиугольник, построенный из пяти зеркал, которые могут чередовать длинные и короткие ребра, и p10 , изотоксальный декагон, построенный с равными длинами ребер, но вершины чередуют два разных внутренних угла. Эти две формы двойственны друг другу и имеют половину порядка симметрии правильного десятиугольника.

Диссекция

10-кубовая проекция	40 ромбовидное рассечение

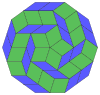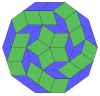Коксетер утверждает, что любой зоногон (2- метровый угольник, противоположные стороны которого параллельны и одинаковой длины) можно разрезать на m ( m -1)/2 параллелограмма. ^[8]В частности, это верно для правильных многоугольников с четным числом сторон, и в этом случае все параллелограммы являются ромбами. Для десятиугольника правильного m = 5, и его можно разделить на 10 ромбов, как показано ниже. Это разложение можно рассматривать как 10 из 80 граней в многоугольника Петри плоскости проекции 5-куба . В основе рассечения лежат 10 из 30 граней ромботриаконтаэдра . Список OEIS : A006245 определяет количество решений как 62, с 2 ориентациями для первой симметричной формы и 10 ориентациями для остальных 6.

Правильный десятиугольник, разрезанный на 10 ромбов.
5-куб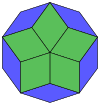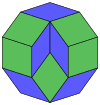

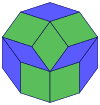Наклон десятиугольника

3 правильных косых зигзагообразных десятиугольника
{5}#{ }	{5/2}#{ }	{5/3}#{ }

Правильный косой десятиугольник рассматривается как зигзагообразные края пятиугольной антипризмы , пентаграммной антипризмы и пентаграммной скрещенной антипризмы .

Косой десятиугольник — это косой многоугольник с 10 вершинами и ребрами, но не расположенный в одной плоскости. Внутренняя часть такого десятиугольника обычно не определена. Косой зигзагообразный десятиугольник имеет вершины, чередующиеся в двух параллельных плоскостях.

Правильный косой десятиугольник является вершинно-транзитивным с равными длинами ребер. В трехмерном измерении это будет зигзагообразный косой декагон, который можно увидеть в вершинах и боковых краях пятиугольной антипризмы , пентаграммной антипризмы и пентаграммной скрещенной антипризмы с тем же D _5d , [2 ⁺,10] симметрия, порядок 20.

Их также можно увидеть в этих четырех выпуклых многогранниках с икосаэдрической симметрией . Многоугольники по периметру этих проекций представляют собой правильные косые десятиугольники.

Ортогональные проекции многогранников на оси 5-го порядка.
Додекаэдр	Икосаэдр	Икосододекаэдр	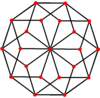Ромбический триаконтаэдр

Полигоны Петри

Правильный косой десятиугольник — это многоугольник Петри для многих многогранников более высокой размерности, показанный в этих ортогональных проекциях на различные плоскости Кокстера : ^[9] Число сторон в многоугольнике Петри равно Коксетера числу h для каждого семейства симметрии.

A_А9	Д ₆		Б ₅
9-симплекс	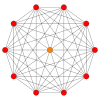4 ₁₁	1 ₃₁	5-ортоплекс	5-куб

См. также

Десятиугольное число и центрированное десятиугольное число , фигурные числа, созданные по образцу десятиугольника.
Декаграмма — звездчатый многоугольник с тем же положением вершин, что и у обычного десятиугольника.

Ссылки

^ Перейти обратно: ^а ^б Сайдботэм, Томас Х. (2003), Математика от А до Я: Основное руководство , John Wiley & Sons, стр. 146, ISBN 9780471461630 .
^ Веннингер, Магнус Дж. (1974), Модели многогранников , издательство Кембриджского университета, стр. 9, ISBN 9780521098595 .
^ Элементы плоской и сферической тригонометрии , Общество содействия христианскому знанию, 1850, с. 59 . Обратите внимание, что этот источник использует a в качестве длины ребра и дает аргумент котангенса как угол в градусах, а не в радианах.
^ Ладлоу, Генри Х. (1904), Геометрическое построение правильного десятиугольника и пятиугольника, вписанных в круг , The Open Court Publishing Co.
^ Перейти обратно: ^а ^б Грин, Генри (1861), Плоская геометрия Евклида, Книги III – VI, Практическое применение, или Градации Евклида, Часть II , Лондон: Simpkin, Marshall, & CO., стр. 116 . Проверено 10 февраля 2016 г.
^ Перейти обратно: ^а ^б Келлер, Юрген (2005), Правильный десятиугольник, → 3-й раздел «Формулы, если дана сторона a ...» (на немецком языке) . Проверено 10 февраля 2016 г.
^ Джон Х. Конвей, Хайди Бургель, Хаим Гудман-Штраус , (2008) Симметрии вещей, ISBN 978-1-56881-220-5 (Глава 20, Обобщенные символы Шефли, Типы симметрии многоугольника, стр. 275-278)
^ Коксетер , Математические развлечения и очерки, тринадцатое издание, стр.141
^ Коксетер, Правильные многогранники, многоугольник Петри 12.4, стр. 223-226.

Внешние ссылки

Вайсштейн, Эрик В. «Декагон» . Математический мир .
Определение и свойства десятиугольника С интерактивной анимацией

[sidebotham-1] Перейти обратно: ^а ^б Сайдботэм, Томас Х. (2003), Математика от А до Я: Основное руководство , John Wiley & Sons, стр. 146, ISBN 9780471461630 .

[2] Веннингер, Магнус Дж. (1974), Модели многогранников , издательство Кембриджского университета, стр. 9, ISBN 9780521098595 .

[3] Элементы плоской и сферической тригонометрии , Общество содействия христианскому знанию, 1850, с. 59 . Обратите внимание, что этот источник использует a в качестве длины ребра и дает аргумент котангенса как угол в градусах, а не в радианах.

[ludlow-4] Ладлоу, Генри Х. (1904), Геометрическое построение правильного десятиугольника и пятиугольника, вписанных в круг , The Open Court Publishing Co.

[Henry_Green-5] Перейти обратно: ^а ^б Грин, Генри (1861), Плоская геометрия Евклида, Книги III – VI, Практическое применение, или Градации Евклида, Часть II , Лондон: Simpkin, Marshall, & CO., стр. 116 . Проверено 10 февраля 2016 г.

[Jürgen_Köller-6] Перейти обратно: ^а ^б Келлер, Юрген (2005), Правильный десятиугольник, → 3-й раздел «Формулы, если дана сторона a ...» (на немецком языке) . Проверено 10 февраля 2016 г.

[7] Джон Х. Конвей, Хайди Бургель, Хаим Гудман-Штраус , (2008) Симметрии вещей, ISBN 978-1-56881-220-5 (Глава 20, Обобщенные символы Шефли, Типы симметрии многоугольника, стр. 275-278)

[8] Коксетер , Математические развлечения и очерки, тринадцатое издание, стр.141

[9] Коксетер, Правильные многогранники, многоугольник Петри 12.4, стр. 223-226.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]