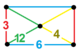
Паракомпактные однородные соты

Пример обычных паракомпактных сот

{3,3,6}	{6,3,3}	{4,3,6}	{6,3,4}
{5,3,6}	{6,3,5}	{6,3,6}	{3,6,3}
{4,4,3}	{3,4,4}	{4,4,4}

В геометрии однородные соты в гиперболическом пространстве представляют собой мозаику из выпуклых многогранника однородных ячеек . В трехмерном гиперболическом пространстве существует 23 групп Кокстера семейства паракомпактных однородных сот, порожденных как конструкции Витхоффа и представленных кольцевыми перестановками диаграмм Кокстера для каждого семейства. Эти семейства могут создавать однородные соты с бесконечными или неограниченными гранями или фигурами вершин , включая идеальные вершины на бесконечности, аналогично гиперболическим однородным мозаикам в 2 измерениях .

Обычные паракомпактные соты

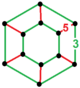
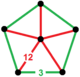
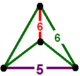
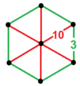
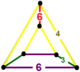
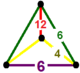
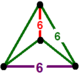
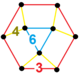
Единого паракомпакта H ³ соты, 11 являются регулярными , что означает, что их группа симметрий действует транзитивно на их флагах. Они имеют символ Шлефли {3,3,6}, {6,3,3}, {3,4,4}, {4,4,3}, {3,6,3}, {4,3,6. }, {6,3,4}, {4,4,4}, {5,3,6}, {6,3,5} и {6,3,6} и показаны ниже. Четыре имеют конечные идеальные многогранные ячейки: {3,3,6}, {4,3,6}, {3,4,4} и {5,3,6}.

Имя	Шлефли Символ {п, д, г}	Коксетер	Клетка тип {п, д}	Лицо тип {р}	Край фигура {р}	Вертекс фигура {q,r}	Двойной	Коксетер группа
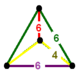
Тетраэдрические соты порядка 6	{3,3,6}		{3,3}	{3}	{6}	{3,6}	{6,3,3}	[6,3,3]
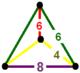
Шестиугольная сотовая плитка	{6,3,3}		{6,3}	{6}	{3}	{3,3}	{3,3,6}
Октаэдрические соты порядка 4	{3,4,4}		{3,4}	{3}	{4}	{4,4}	{4,4,3}	[4,4,3]
Квадратная сотовая плитка	{4,4,3}		{4,4}	{4}	{3}	{4,3}	{3,4,4}
Треугольные соты для плитки	{3,6,3}		{3,6}	{3}	{3}	{6,3}	Самодвойственный	[3,6,3]
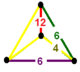
Заказ-6 куб.сот	{4,3,6}		{4,3}	{4}	{4}	{3,6}	{6,3,4}	[6,3,4]
Шестиугольная плитка Order-4 сотовая	{6,3,4}		{6,3}	{6}	{4}	{3,4}	{4,3,6}
Заказать-4 квадратные соты для плитки	{4,4,4}		{4,4}	{4}	{4}	{4,4}	Самодвойственный	[4,4,4]
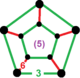
Додекаэдрические соты порядка 6	{5,3,6}		{5,3}	{5}	{5}	{3,6}	{6,3,5}	[6,3,5]
Шестиугольная плитка Орден-5 сотовая	{6,3,5}		{6,3}	{6}	{5}	{3,5}	{5,3,6}
Шестиугольная плитка Орден-6 сотовая	{6,3,6}		{6,3}	{6}	{6}	{3,6}	Самодвойственный	[6,3,6]

Группы Кокстера паракомпактных однородных сот

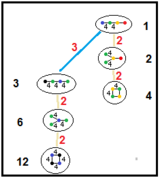Эти графики показывают отношения подгрупп паракомпактных гиперболических групп Кокстера. Подгруппы второго порядка представляют собой делящий пополам тетраэдр Гурса плоскостью зеркальной симметрии.

Это полный перечень 151 уникальных паракомпактных однородных сот Витоффа, созданных из тетраэдрических фундаментальных доменов (паракомпактных групп Кокстера 4-го ранга). Соты проиндексированы здесь для перекрестных ссылок на повторяющиеся формы, в скобках заключены неосновные конструкции.

Чередования . перечислены, но либо повторяются, либо не приводят к единообразным решениям Чередование одиночных отверстий представляет собой операцию удаления зеркала. Если удалить конечный узел, создается другое симплексное (тетраэдрическое) семейство. Если дырка имеет две ветви, образуется многогранник Винберга , хотя к симплексным группам относятся только многогранники Винберга с зеркальной симметрией, а их однородные соты систематически не исследовались. Эти несимплектические (пирамидальные) группы Кокстера на этой странице не перечисляются, за исключением частных случаев полугрупп тетраэдрических. Шесть однородных сот, возникающих здесь в виде чередований, пронумерованы от 152 до 157, после 151 формы Витоффа, не требующей чередования для своего построения.

Краткое описание тетраэдрической гиперболической паракомпактной группы

Группа Коксетера		Симплекс объем	Подгруппа коммутатора	Уникальное количество сот
[6,3,3]		0.0422892336	[1 + ,6,(3,3) + ] = [3,3 [3] ] +	15
[4,4,3]		0.0763304662	[1 + ,4,1 + ,4,3 + ]	15
[3,3 [3] ]		0.0845784672	[3,3 [3] ] +	4
[6,3,4]		0.1057230840	[1 + ,6,3 + ,4,1 + ] = [3 []х[] ] +	15
[3,4 1,1 ]		0.1526609324	[3 + ,4 1 + ,1 + ]	4
[3,6,3]		0.1691569344	[3 + ,6,3 + ]	8
[6,3,5]		0.1715016613	[1 + ,6,(3,5) + ] = [5,3 [3] ] +	15
[6,3 1,1 ]		0.2114461680	[1 + ,6,(3 1,1 ) + ] = [3 []х[] ] +	4
[4,3 [3] ]		0.2114461680	[1 + ,4,3 [3] ] + = [3 []х[] ] +	4
[4,4,4]		0.2289913985	[4 + ,4 + ,4 + ] +	6
[6,3,6]		0.2537354016	[1 + ,6,3 + ,6,1 + ] = [3 [3,3] ] +	8
[(4,4,3,3)]		0.3053218647	[(4,1 + ,4,(3,3) + )]	4
[5,3 [3] ]		0.3430033226	[5,3 [3] ] +	4
[(6,3,3,3)]		0.3641071004	[(6,3,3,3)] +	9
[3 []х[] ]		0.4228923360	[3 []х[] ] +	1
[4 1,1,1 ]		0.4579827971	[1 + ,4 1 + ,1 + ,1 + ]	0
[6,3 [3] ]		0.5074708032	[1 + ,6,3 [3] ] = [3 [3,3] ] +	2
[(6,3,4,3)]		0.5258402692	[(6,3 + ,4,3 + )]	9
[(4,4,4,3)]		0.5562821156	[(4,1 + ,4,1 + ,4,3 + )]	9
[(6,3,5,3)]		0.6729858045	[(6,3,5,3)] +	9
[(6,3,6,3)]		0.8457846720	[(6,3 + ,6,3 + )]	5
[(4,4,4,4)]		0.9159655942	[(4 + ,4 + ,4 + ,4 + )]	1
[3 [3,3] ]		1.014916064	[3 [3,3] ] +	0

Полный список несимплектических (нететраэдрических) паракомпактных групп Кокстера был опубликован П. Тумаркиным в 2003 году. Наименьшая паракомпактная форма в H ³ может быть представлено или , или [∞,3,3,∞], которые можно построить зеркальным удалением паракомпактной гиперболической группы [3,4,4] как [3,4,1 ⁺ ,4] : = . Удвоенная фундаментальная область превращается из тетраэдра в четырехугольную пирамиду. Еще одна пирамида или , построенный как [4,4,1 ⁺ ,4] = [∞,4,4,∞] : = .

Удаление зеркала из некоторых циклических гиперболических графов Кокстера становится графами-бабочками: [(3,3,4,1 ⁺ ,4)] = [((3,∞,3)),((3,∞,3))] или , [(3,4,4,1 ⁺ ,4)] = [((4,∞,3)),((3,∞,4))] или , [(4,4,4,1 ⁺ ,4)] = [((4,∞,4)),((4,∞,4))] или . = , = , = .

Другая несимплектическая полугруппа - это ↔ .

Радикальная несимплектическая подгруппа — это ↔ , которую можно удвоить в область треугольной призмы как ↔ .

Краткое описание пирамидальной гиперболической паракомпактной группы

Измерение	Классифицировать	Графики
ЧАС 3	5	| | | | | | | | | | | | | | | | | | | | | | | | | | |

Линейные графики

[6,3,3] семья

#	Сотовое имя Диаграмма Кокстера : Символ Шлефли	Ячейки по местоположению (и посчитаем вокруг каждой вершины)				Вершинная фигура	Картина
		1	2	3	4
1	шестиугольный {6,3,3}	-	-	-	(4) (6.6.6)	Тетраэдр
2	выпрямленный шестиугольный t 1 {6,3,3} или r{6,3,3}	(2) (3.3.3)	-	-	(3) (3.6.3.6)	Треугольная призма
3	выпрямленный тетраэдр шестого порядка т 1 {3,3,6} или r{3,3,6}	(6) (3.3.3.3)	-	-	(2) (3.3.3.3.3.3)	Шестиугольная призма
4	тетраэдр 6-го порядка {3,3,6}	(∞) (3.3.3)	-	-	-	Треугольная плитка
5	усеченный шестиугольный т 0,1 {6,3,3} или т{6,3,3}	(1) (3.3.3)	-	-	(3) (3.12.12)	Треугольная пирамида
6	согнутый шестиугольный т 0,2 {6,3,3} или рр{6,3,3}	(1) 3.3.3.3	(2) (4.4.3)	-	(2) (3.4.6.4)
7	суженный шестиугольный т 0,3 {6,3,3}	(1) (3.3.3)	(3) (4.4.3)	(3) (4.4.6)	(1) (6.6.6)
8	согнутый тетраэдр порядка 6 т 0,2 {3,3,6} или рр{3,3,6}	(1) (3.4.3.4)	-	(2) (4.4.6)	(2) (3.6.3.6)
9	усеченный шестиугольник т 1,2 {6,3,3} или 2т{6,3,3}	(2) (3.6.6)	-	-	(2) (6.6.6)
10	усеченный тетраэдр шестого порядка т 0,1 {3,3,6} или т{3,3,6}	(6) (3.6.6)	-	-	(1) (3.3.3.3.3.3)
11	количественно усеченный шестиугольный т 0,1,2 {6,3,3} или тр{6,3,3}	(1) (3.6.6)	(1) (4.4.3)	-	(2) (4.6.12)
12	необрезанный шестиугольный т 0,1,3 {6,3,3}	(1) (3.4.3.4)	(2) (4.4.3)	(1) (4.4.12)	(1) (3.12.12)
13	неусеченный тетраэдр порядка 6 т 0,1,3 {3,3,6}	(1) (3.6.6)	(1) (4.4.6)	(2) (4.4.6)	(1) (3.4.6.4)
14	усеченный тетраэдр порядка 6 т 0,1,2 {3,3,6} или тр{3,3,6}	(2) (4.6.6)	-	(1) (4.4.6)	(1) (6.6.6)
15	всеусеченный шестиугольный т 0,1,2,3 {6,3,3}	(1) (4.6.6)	(1) (4.4.6)	(1) (4.4.12)	(1) (4.6.12)

Альтернативные формы

#	Сотовое имя Диаграмма Кокстера : Символ Шлефли	Ячейки по местоположению (и посчитаем вокруг каждой вершины)					Вершинная фигура	Картина
		1	2	3	4	Все
[137]	чередующийся шестиугольный ( ↔ ) =	-	-		(4) (3.3.3.3.3.3)	(4) (3.3.3)	(3.6.6)
[138]	Кантик шестиугольный ↔	(1) (3.3.3.3)	-		(2) (3.6.3.6)	(2) (3.6.6)
[139]	рунчик шестиугольный ↔	(1) (4.4.4)	(1) (4.4.3)		(1) (3.3.3.3.3.3)	(3) (3.4.3.4)
[140]	рунический шестиугольный ↔	(1) (3.6.6)	(1) (4.4.3)		(1) (3.6.3.6)	(2) (4.6.6)
Неоднородный	курносый выпрямленный тетраэдр шестого порядка ↔ ср{3,3,6}					Ирр. (3.3.3)
Неоднородный	Кантик курносый, тетраэдрический порядка 6 ср 3 {3,3,6}
Неоднородный	тетраэдрический омниснуб порядка 6 чт 0,1,2,3 {6,3,3}					Ирр. (3.3.3)

[6,3,4] семья

Существует 15 форм, порожденных кольцевыми перестановками группы Коксетера : [6,3,4] или

#	Название сот Диаграмма Кокстера Символ Шлефли	Ячейки по расположению и количеству на вершину				Вершинная фигура	Картина
		0	1	2	3
16	(Обычный) шестиугольный порядка 4 {6,3,4}	-	-	-	(8) (6.6.6)	(3.3.3.3)
17	выпрямленный порядка 4 шестиугольный t 1 {6,3,4} или r{6,3,4}	(2) (3.3.3.3)	-	-	(4) (3.6.3.6)	(4.4.4)
18	ректифицированный заказ-6 куб. t 1 {4,3,6} или r{4,3,6}	(6) (3.4.3.4)	-	-	(2) (3.3.3.3.3.3)	(6.4.4)
19	заказ-6 куб. {4,3,6}	(20) (4.4.4)	-	-	-	(3.3.3.3.3.3)
20	усеченный шестиугольный порядка 4 т 0,1 {6,3,4} или т{6,3,4}	(1) (3.3.3.3)	-	-	(4) (3.12.12)
21	битусеченный порядка 6 кубических т 1,2 {6,3,4} или 2т{6,3,4}	(2) (4.6.6)	-	-	(2) (6.6.6)
22	усеченный порядка-6 куб. т 0,1 {4,3,6} или т{4,3,6}	(6) (3.8.8)	-	-	(1) (3.3.3.3.3.3)
23	согнутый 4-го порядка шестиугольный т 0,2 {6,3,4} или рр{6,3,4}	(1) (3.4.3.4)	(2) (4.4.4)	-	(2) (3.4.6.4)
24	согнутого порядка-6 куб. т 0,2 {4,3,6} или рр{4,3,6}	(2) (3.4.4.4)	-	(2) (4.4.6)	(1) (3.6.3.6)
25	сморщенный порядка-6 куб. т 0,3 {6,3,4}	(1) (4.4.4)	(3) (4.4.4)	(3) (4.4.6)	(1) (6.6.6)
26	усеченный шестиугольный порядка 4 т 0,1,2 {6,3,4} или тр{6,3,4}	(1) (4.6.6)	(1) (4.4.4)	-	(2) (4.6.12)
27	кантиусеченный порядка 6 куб. т 0,1,2 {4,3,6} или тр{4,3,6}	(2) (4.6.8)	-	(1) (4.4.6)	(1) (6.6.6)
28	неусеченный шестиугольный порядка 4 т 0,1,3 {6,3,4}	(1) (3.4.4.4)	(1) (4.4.4)	(2) (4.4.12)	(1) (3.12.12)
29	ограненный-усеченный порядка 6 куб. т 0,1,3 {4,3,6}	(1) (3.8.8)	(2) (4.4.8)	(1) (4.4.6)	(1) (3.4.6.4)
30	всеусеченный порядка-6 куб. т 0,1,2,3 {6,3,4}	(1) (4.6.8)	(1) (4.4.8)	(1) (4.4.12)	(1) (4.6.12)

Альтернативные формы

#	Название сот Диаграмма Кокстера Символ Шлефли	Ячейки по расположению и количеству на вершину					Вершинная фигура	Картина
		0	1	2	3	Все
[87]	чередующийся порядок-6 куб. ↔ ч{4,3,6}	(3.3.3)				(3.3.3.3.3.3)	(3.6.3.6)
[88]	кантический порядок-6 куб. ↔ ч 2 {4,3,6}	(2) (3.6.6)	-	-	(1) (3.6.3.6)	(2) (6.6.6)
[89]	рунич порядка-6 куб. ↔ ч 3 {4,3,6}	(1) (3.3.3)	-	-	(1) (6.6.6)	(3) (3.4.6.4)
[90]	ранцикантический порядок-6 куб. ↔ ч 2,3 {4,3,6}	(1) (3.6.6)	-	-	(1) (3.12.12)	(2) (4.6.12)
[141]	чередующийся шестиугольный порядок 4 ↔ ↔ ч{6,3,4}	-	-		(3.3.3.3.3.3)	(3.3.3.3)	(4.6.6)
[142]	кантический порядок-4 шестиугольный ↔ ↔ ч 1 {6,3,4}	(1) (3.4.3.4)	-		(2) (3.6.3.6)	(2) (4.6.6)
[143]	рунцич порядка 4 шестиугольный ↔ ч 3 {6,3,4}	(1) (4.4.4)	(1) (4.4.3)		(1) (3.3.3.3.3.3)	(3) (3.4.4.4)
[144]	рунцикантический порядок-4 шестиугольный ↔ ч 2,3 {6,3,4}	(1) (3.8.8)	(1) (4.4.3)		(1) (3.6.3.6)	(2) (4.6.8)
[151]	четверть порядка-4 шестиугольная ↔ д{6,3,4}	(3)	(1)	-	(1)	(3)
Неоднородный	биснуб заказ-6 куб. ↔ 2с{4,3,6}	(3.3.3.3.3)	-	-	(3.3.3.3.3.3)	+ (3.3.3)
Неоднородный	рунцич двузубый порядка -6 куб.
Неоднородный	курносый ректификованный порядка 6 куб. ↔ ср{4,3,6}	(3.3.3.3.3)	(3.3.3)	(3.3.3.3)	(3.3.3.3.6)	+ (3.3.3)
Неоднородный	рунцич курносый ректификованный порядка 6 куб. ср 3 {4,3,6}
Неоднородный	коротконосый выпрямленный шестигранный порядка 4 ↔ ср{6,3,4}	(3.3.3.3.3.3)	(3.3.3)	-	(3.3.3.3.6)	+ (3.3.3)
Неоднородный	runcisnub выпрямленный шестиугольный порядка 4 ср 3 {6,3,4}
Неоднородный	омниснуб ректифицированный заказ-6 куб. чт 0,1,2,3 {6,3,4}	(3.3.3.3.4)	(3.3.3.4)	(3.3.3.6)	(3.3.3.3.6)	+ (3.3.3)

[6,3,5] семья

#	Сотовое имя Диаграмма Кокстера Символ Шлефли	Ячейки по местоположению (и посчитаем вокруг каждой вершины)				Вершинная фигура	Картина
		0	1	2	3
31	шестиугольный порядка 5 {6,3,5}	-	-	-	(20) (6) 3	Икосаэдр
32	выпрямленный порядка 5 шестиугольный t 1 {6,3,5} или r{6,3,5}	(2) (3.3.3.3.3)	-	-	(5) (3.6) 2	(5.4.4)
33	исправленный додекаэдр порядка 6 t 1 {5,3,6} или r{5,3,6}	(5) (3.5.3.5)	-	-	(2) (3) 6	(6.4.4)
34	додекаэдр порядка 6 {5,3,6}	(5.5.5)	-	-	-	(∞) (3) 6
35	усеченный шестиугольный порядка 5 т 0,1 {6,3,5} или т{6,3,5}	(1) (3.3.3.3.3)	-	-	(5) 3.12.12
36	согнутый 5-го порядка шестиугольный т 0,2 {6,3,5} или рр{6,3,5}	(1) (3.5.3.5)	(2) (5.4.4)	-	(2) 3.4.6.4
37	сморщенный додекаэдр порядка 6 т 0,3 {6.3.5}	(1) (5.5.5)	-	(6) (6.4.4)	(1) (6) 3
38	согнутый додекаэдр порядка 6 т 0,2 {5,3,6} или рр{5,3,6}	(2) (4.3.4.5)	-	(2) (6.4.4)	(1) (3.6) 2
39	усеченный додекаэдр порядка 6 т 1,2 {6,3,5} или 2т{6,3,5}	(2) (5.6.6)	-	-	(2) (6) 3
40	усеченный додекаэдр порядка 6 т 0,1 {5,3,6} или т{5,3,6}	(6) (3.10.10)	-	-	(1) (3) 6
41	усеченный шестиугольный порядка 5 т 0,1,2 {6,3,5} или тр{6,3,5}	(1) (5.6.6)	(1) (5.4.4)	-	(2) 4.6.10
42	шестиугольный неусеченный порядка 5 т 0,1,3 {6,3,5}	(1) (4.3.4.5)	(1) (5.4.4)	(2) (12.4.4)	(1) 3.12.12
43	неусеченный додекаэдр порядка 6 т 0,1,3 {5,3,6}	(1) (3.10.10)	(1) (10.4.4)	(2) (6.4.4)	(1) 3.4.6.4
44	кантиусеченный додекаэдр порядка 6 т 0,1,2 {5,3,6} или тр{5,3,6}	(1) (4.6.10)	-	(2) (6.4.4)	(1) (6) 3
45	всеусеченный додекаэдр порядка 6 т 0,1,2,3 {6,3,5}	(1) (4.6.10)	(1) (10.4.4)	(1) (12.4.4)	(1) 4.6.12

Альтернативные формы

#	Сотовое имя Диаграмма Кокстера Символ Шлефли	Ячейки по местоположению (и посчитаем вокруг каждой вершины)					Вершинная фигура	Картина
		0	1	2	3	Все
[145]	чередующийся шестиугольный порядок 5 ↔ ч{6,3,5}	-	-	-	(20) (3) 6	(12) (3) 5	(5.6.6)
[146]	кантический порядок-5 шестиугольный ↔ ч 2 {6,3,5}	(1) (3.5.3.5)	-		(2) (3.6.3.6)	(2) (5.6.6)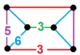
[147]	рунцич порядка 5 шестиугольный ↔ ч 3 {6,3,5}	(1) (5.5.5)	(1) (4.4.3)		(1) (3.3.3.3.3.3)	(3) (3.4.5.4)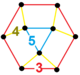
[148]	рунцикантический порядок-5 шестиугольный ↔ ч 2,3 {6,3,5}	(1) (3.10.10)	(1) (4.4.3)		(1) (3.6.3.6)	(2) (4.6.10)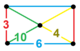
Неоднородный	курносый выпрямленный додекаэдр порядка 6 ↔ ср{5,3,6}	(3.3.5.3.5)	-	(3.3.3.3)	(3.3.3.3.3.3)	ирр. тет
Неоднородный	омниснуб порядка 5 шестиугольный чт 0,1,2,3 {6,3,5}	(3.3.5.3.5)	(3.3.3.5)	(3.3.3.6)	(3.3.6.3.6)	ирр. тет

[6,3,6] семья

Существует 9 форм, порожденных кольцевыми перестановками группы Кокстера : [6,3,6] или

#	Название сот Диаграмма Кокстера Символ Шлефли	Ячейки по расположению и количеству на вершину				Вершинная фигура	Картина
		0	1	2	3
46	шестиугольный порядка 6 {6,3,6}	-	-	-	(20) (6.6.6)	(3.3.3.3.3.3)
47	выпрямленный шестиугольный порядка 6 t 1 {6,3,6} или r{6,3,6}	(2) (3.3.3.3.3.3)	-	-	(6) (3.6.3.6)	(6.4.4)
48	усеченный шестиугольный порядка 6 т 0,1 {6,3,6} или т{6,3,6}	(1) (3.3.3.3.3.3)	-	-	(6) (3.12.12)
49	согнутый шестиугольный порядок-6 т 0,2 {6,3,6} или рр{6,3,6}	(1) (3.6.3.6)	(2) (4.4.6)	-	(2) (3.6.4.6)
50	Шестигранный, шестигранный порядка 6 т 0,3 {6,3,6}	(1) (6.6.6)	(3) (4.4.6)	(3) (4.4.6)	(1) (6.6.6)
51	усеченный шестиугольный порядка 6 т 0,1,2 {6,3,6} или тр{6,3,6}	(1) (6.6.6)	(1) (4.4.6)	-	(2) (4.6.12)
52	шестиугольный неусеченный порядка 6 т 0,1,3 {6,3,6}	(1) (3.6.4.6)	(1) (4.4.6)	(2) (4.4.12)	(1) (3.12.12)
53	всеусеченный шестиугольный порядка 6 т 0,1,2,3 {6,3,6}	(1) (4.6.12)	(1) (4.4.12)	(1) (4.4.12)	(1) (4.6.12)
[1]	усеченный шестиугольный порядка 6 ↔ ↔ т 1,2 {6,3,6} или 2т{6,3,6}	(2) (6.6.6)	-	-	(2) (6.6.6)

Альтернативные формы

#	Название сот Диаграмма Кокстера Символ Шлефли	Ячейки по расположению и количеству на вершину					Вершинная фигура	Картина
		0	1	2	3	Все
[47]	выпрямленный шестиугольный порядка 6 ↔ ↔ д{6,3,6} = г{6,3,6}	(2) (3.3.3.3.3.3)	-	-	(6) (3.6.3.6)		(6.4.4)
[54]	треугольный ( ↔ ) = ч{6,3,6} = {3,6,3}	-	-	-	(3.3.3.3.3.3)	(3.3.3.3.3.3)	{6,3}
[55]	Кантический порядок-6 шестиугольный ( ↔ ) = ч 2 {6,3,6} = r{3,6,3}	(1) (3.6.3.6)	-	(2) (6.6.6)	(2) (3.6.3.6)
[149]	рунцич порядка 6 шестиугольный ↔ ч 3 {6,3,6}	(1) (6.6.6)	(1) (4.4.3)	(3) (3.4.6.4)	(1) (3.3.3.3.3.3)
[150]	рунцикантический порядок-6 шестиугольный ↔ ч 2,3 {6,3,6}	(1) (3.12.12)	(1) (4.4.3)	(2) (4.6.12)	(1) (3.6.3.6)
[137]	чередующийся шестиугольный ( ↔ ↔ ) = 2с{6,3,6} = ч{6,3,3}	(3.3.3.3.6)	-	-	(3.3.3.3.6)	+ (3.3.3)	(3.6.6)
Неоднородный	коротконосый выпрямленный шестигранный порядка 6 ср{6,3,6}	(3.3.3.3.3.3)	(3.3.3.3)	-	(3.3.3.3.6)	+ (3.3.3)
Неоднородный	чередующиеся сусечатые шестиугольные порядка 6 хт 0.3 {6,3,6}	(3.3.3.3.3.3)	(3.3.3.3)	(3.3.3.3)	(3.3.3.3.3.3)	+ (3.3.3)
Неоднородный	omnisnub порядка 6 шестиугольный чт 0,1,2,3 {6,3,6}	(3.3.3.3.6)	(3.3.3.6)	(3.3.3.6)	(3.3.3.3.6)	+ (3.3.3)

[3,6,3] семья

Существует 9 форм, порожденных кольцевыми перестановками группы Кокстера : [3,6,3] или

#	Сотовое имя Диаграмма Кокстера и символ Шлефли	Количество ячеек/вершина и позиции в сотах				Вершинная фигура	Картина
		0	1	2	3
54	треугольный {3,6,3}	-	-	-	(∞) {3,6}	{6,3}
55	выпрямленный треугольный t 1 {3,6,3} или r{3,6,3}	(2) (6) 3	-	-	(3) (3.6) 2	(3.4.4)
56	согнутый треугольный т 0,2 {3,6,3} или рр{3,6,3}	(1) (3.6) 2	(2) (4.4.3)	-	(2) (3.6.4.6)
57	суженный треугольный т 0,3 {3,6,3}	(1) (3) 6	(6) (4.4.3)	(6) (4.4.3)	(1) (3) 6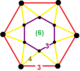
58	усеченный треугольный т 1,2 {3,6,3} или 2т{3,6,3}	(2) (3.12.12)	-	-	(2) (3.12.12)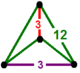
59	скошенный треугольный т 0,1,2 {3,6,3} или тр{3,6,3}	(1) (3.12.12)	(1) (4.4.3)	-	(2) (4.6.12)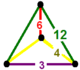
60	скругленный треугольный т 0,1,3 {3,6,3}	(1) (3.6.4.6)	(1) (4.4.3)	(2) (4.4.6)	(1) (6) 3
61	всеусеченный треугольный т 0,1,2,3 {3,6,3}	(1) (4.6.12)	(1) (4.4.6)	(1) (4.4.6)	(1) (4.6.12)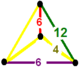
[1]	усеченный треугольный ↔ ↔ т 0,1 {3,6,3} или т{3,6,3} = {6,3,3}	(1) (6) 3	-	-	(3) (6) 3	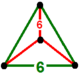{3,3}

Альтернативные формы

#	Сотовое имя Диаграмма Кокстера и символ Шлефли	Количество ячеек/вершина и позиции в сотах					Вершинная фигура	Картина
		0	1	2	3	Все
[56]	согнутый треугольный = с 2 {3,6,3}	(1) (3.6) 2	-	-	(2) (3.6.4.6)	(3.4.4)
[60]	скругленный треугольный = с 2,3 {3,6,3}	(1) (6) 3	-	(1) (4.4.3)	(1) (3.6.4.6)	(2) (4.4.6)
[137]	чередующийся шестиугольный ( ↔ ) = ( ↔ ) с{3,6,3}	(3) 6	-	-	(3) 6	+ (3) 3	(3.6.6)
Чешуевидный	тонциснуб треугольный с 3 {3,6,3}	г{6,3}	-	(3.4.4)	(3) 6	трикуп
Неоднородный	omnisnub треугольная сотовая плитка чт 0,1,2,3 {3,6,3}	(3.3.3.3.6)	(3) 4	(3) 4	(3.3.3.3.6)	+ (3) 3

[4,4,3] семья

Существует 15 форм, порожденных кольцевыми перестановками группы Коксетера : [4,4,3] или

#	Сотовое имя Диаграмма Кокстера и символ Шлефли	Количество ячеек/вершина и позиции в сотах				Вершинная фигура	Картина
		0	1	2	3
62	квадрат = {4,4,3}	-	-	-	(6)	Куб
63	выпрямленный квадрат = t 1 {4,4,3} или r{4,4,3}	(2)	-	-	(3)	Треугольная призма
64	выпрямленный октаэдрический порядка 4 t 1 {3,4,4} или r{3,4,4}	(4)	-	-	(2)
65	октаэдрический порядок-4 {3,4,4}	(∞)	-	-	-
66	усеченный квадрат = т 0,1 {4,4,3} или т{4,4,3}	(1)	-	-	(3)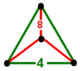
67	усеченный октаэдр порядка 4 т 0,1 {3,4,4} или т{3,4,4}	(4)	-	-	(1)
68	усеченный квадрат т 1,2 {4,4,3} или 2т{4,4,3}	(2)	-	-	(2)
69	изогнутый квадрат т 0,2 {4,4,3} или рр{4,4,3}	(1)	(2)	-	(2)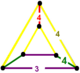
70	согнутый октаэдр порядка 4 т 0,2 {3,4,4} или рр{3,4,4}	(2)	-	(2)	(1)
71	сморщенный квадрат т 0,3 {4,4,3}	(1)	(3)	(3)	(1)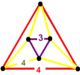
72	наклонный квадрат т 0,1,2 {4,4,3} или тр{4,4,3}	(1)	(1)	-	(2)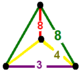
73	наклонно-усеченный октаэдр порядка 4 т 0,1,2 {3,4,4} или тр{3,4,4}	(2)	-	(1)	(1)
74	неровный квадрат т 0,1,3 {4,4,3}	(1)	(1)	(2)	(1)
75	неусеченный октаэдр порядка 4 т 0,1,3 {3,4,4}	(1)	(2)	(1)	(1)
76	всеусеченный квадрат т 0,1,2,3 {4,4,3}	(1)	(1)	(1)	(1)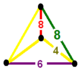

Альтернативные формы

#	Сотовое имя Диаграмма Кокстера и символ Шлефли	Количество ячеек/вершина и позиции в сотах					Вершинная фигура	Картина
		0	1	2	3	Все
[83]	чередующийся квадрат ↔ ч{4,4,3}	-	-	-		{4,3}	(4.3.4.3)
[84]	Кантическая площадь ↔ ч 2 {4,4,3}	(3.4.3.4)	-	(3.8.8)		(4.8.8)
[85]	Рунчичская площадь ↔ ч 3 {4,4,3}	(3.3.3.3)	-	(3.4.4.4)		(4.4.4)
[86]	рунический квадрат ↔	(4.6.6)	-	(3.4.4.4)		(4.8.8)
[153]	чередующийся выпрямленный квадрат ↔ час {4,4,3}		-	-		{}х{3}
157			-	-		{}x{6}
Чешуевидный	курносый порядок-4 октаэдрический = = с{3,4,4}		-	-		{}v{4}
Чешуевидный	октаэдрический порядка 4 runcisnub с 3 {3,4,4}					чашка-4
152	курносый квадрат = с{4,4,3}		-	-		{3,3}
Неоднородный	курносый выпрямленный октаэдрический порядка 4 ср{3,4,4}		-			ирр. {3,3}
Неоднородный	чередующийся пересечённый квадрат чт 0,1,3 {3,4,4}					ирр. {}v{4}
Неоднородный	Омниснубская площадь чт 0,1,2,3 {4,4,3}					ирр. {3,3}

[4,4,4] семья

Существует 9 форм, порожденных кольцевыми перестановками группы Коксетера : [4,4,4] или .

#	Сотовое имя Диаграмма Кокстера и символ Шлефли	Количество ячеек/вершина и позиции в сотах				Симметрия	Вершинная фигура	Картина
		0	1	2	3
77	порядок-4 квадрата {4,4,4}	-	-	-		[4,4,4]	Куб
78	усеченный квадрат порядка 4 т 0,1 {4,4,4} или т{4,4,4}		-	-		[4,4,4]
79	усеченный квадрат порядка 4 т 1,2 {4,4,4} или 2т{4,4,4}		-	-		[[4,4,4]]
80	сморщенный порядка 4 квадрат т 0,3 {4,4,4}					[[4,4,4]]
81	неусеченный квадрат порядка 4 т 0,1,3 {4,4,4}					[4,4,4]
82	всеусеченный квадрат порядка 4 т 0,1,2,3 {4,4,4}					[[4,4,4]]
[62]	квадрат ↔ t 1 {4,4,4} или r{4,4,4}		-	-		[4,4,4]	Квадратная плитка
[63]	выпрямленный квадрат ↔ т 0,2 {4,4,4} или рр{4,4,4}			-		[4,4,4]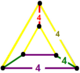
[66]	усеченный квадрат порядка 4 ↔ т 0,1,2 {4,4,4} или тр{4,4,4}			-		[4,4,4]

Альтернативные конструкции

#	Сотовое имя Диаграмма Кокстера и символ Шлефли	Количество ячеек/вершина и позиции в сотах					Симметрия	Вершинная фигура	Картина
		0	1	2	3	Все
[62]	Квадрат ( ↔ ↔ ↔ ) =	(4.4.4.4)	-	-		(4.4.4.4)	[1 + ,4,4,4] =[4,4,4]
[63]	выпрямленный квадрат = с 2 {4,4,4}			-			[4 + ,4,4]
[77]	порядок-4 квадрата ↔ ↔ ↔	-	-	-			[1 + ,4,4,4] =[4,4,4]	Куб
[78]	усеченный квадрат порядка 4 ↔ ↔ ↔	(4.8.8)	-	(4.8.8)	-	(4.4.4.4)	[1 + ,4,4,4] =[4,4,4]
[79]	усеченный квадрат порядка 4 ↔ ↔ ↔	(4.8.8)	-	-	(4.8.8)	(4.8.8)	[1 + ,4,4,4] =[4,4,4]
[81]	усеченная квадратная плитка порядка 4 = с 2,3 {4,4,4}						[4,4,4]
[83]	чередующийся квадрат ( ↔ ) ↔ час {4,4,4}		-	-			[4,1 + ,4,4]	(4.3.4.3)
[104]	порядок четверти-4 квадрата ↔ д{4,4,4}						[[1 + ,4,4,4,1 + ]] =[[4 [4] ]]
153	чередующаяся выпрямленная квадратная плитка ↔ ↔ час{4,4,4}			-			[((2 + ,4,4)),4]
154	чередующаяся квадратная плитка четвертого порядка хт 0.3 {4,4,4}						[[(4,4,4,2 + )]]
Чешуевидный	укладка квадратной плитки в пренебрежительном порядке - 4 с{4,4,4}		-	-			[4 + ,4,4]
Неоднородный	Runcic Snub Order-4 Квадратная плитка с 3 {4,4,4}						[4 + ,4,4]
Неоднородный	укладка квадратной плитки в порядке bisnub - 4 2с{4,4,4}		-	-			[[4,4 + ,4]]
[152]	укладка плоской квадратной плитки ↔ ср{4,4,4}			-			[(4,4) + ,4]
Неоднородный	чередующаяся усеченная квадратная плитка порядка 4 чт 0,1,3 {4,4,4}						[((2,4) + ,4,4)]
Неоднородный	Укладка плитки omnisnub порядка 4 квадратов чт 0,1,2,3 {4,4,4}						[[4,4,4]] +

Трезубцы графы

[3,4 ^1,1 ] семья

Существует 11 форм (из которых только 4 не являются общими с семейством [4,4,3]), порожденных кольцевыми перестановками группы Коксетера :

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)				Вершинная фигура	Картина
		0	1	0'	3
83	чередующийся квадрат ↔	-	-	(4.4.4)	(4.4.4.4)	(4.3.4.3)
84	Кантическая площадь ↔	(3.4.3.4)	-	(3.8.8)	(4.8.8)
85	Рунчичская площадь ↔	(4.4.4.4)	-	(3.4.4.4)	(4.4.4.4)
86	рунический квадрат ↔	(4.6.6)	-	(3.4.4.4)	(4.8.8)
[63]	выпрямленный квадрат ↔	(4.4.4)	-	(4.4.4)	(4.4.4.4)
[64]	выпрямленный октаэдрический порядка 4 ↔	(3.4.3.4)	-	(3.4.3.4)	(4.4.4.4)
[65]	октаэдрический порядок-4 ↔	(4.4.4.4)	-	(4.4.4.4)	-
[67]	усеченный октаэдр порядка 4 ↔	(4.6.6)	-	(4.6.6)	(4.4.4.4)
[68]	усеченный квадрат ↔	(3.8.8)	-	(3.8.8)	(4.8.8)
[70]	согнутый октаэдр порядка 4 ↔	(3.4.4.4)	(4.4.4)	(3.4.4.4)	(4.4.4.4)
[73]	наклонно-усеченный октаэдр порядка 4 ↔	(4.6.8)	(4.4.4)	(4.6.8)	(4.8.8)

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)					Вершинная фигура	Картина
		0	1	0'	3	Все
Чешуевидный	курносый порядок-4 октаэдрический = = с{3,4 1,1 }		-	-		ирр. {}v{4}
Неоднородный	курносый выпрямленный октаэдрический порядка 4 ↔ ср{3,4 1,1 }	(3.3.3.3.4)	(3.3.3)	(3.3.3.3.4)	(3.3.4.3.4)	+ (3.3.3)

[4,4 ^1,1 ] семья

Существует 7 форм (все они являются общими с семейством [4,4,4]), порожденных кольцевыми перестановками группы Коксетера :

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению				Вершинная фигура	Картина
		0	1	0'	3
[62]	Квадрат ( ↔ ) =	(4.4.4.4)	-	(4.4.4.4)	(4.4.4.4)
[62]	Квадрат ( ↔ ) =	(4.4.4.4)	-	(4.4.4.4)	(4.4.4.4)
[63]	выпрямленный квадрат ( ↔ ) =	(4.4.4.4)	(4.4.4)	(4.4.4.4)	(4.4.4.4)
[66]	усеченный квадрат ( ↔ ) =	(4.8.8)	(4.4.4)	(4.8.8)	(4.8.8)
[77]	порядок-4 квадрата ↔	(4.4.4.4)	-	(4.4.4.4)	-
[78]	усеченный квадрат порядка 4 ↔	(4.8.8)	-	(4.8.8)	(4.4.4.4)
[79]	усеченный квадрат порядка 4 ↔	(4.8.8)	-	(4.8.8)	(4.8.8)

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)					Вершинная фигура	Картина
		0	1	0'	3	Все
[77]	порядок-4 квадрата ( ↔ ↔ ) =		-		-	Куб
[78]	усеченный квадрат порядка 4 ( ↔ ) = ( ↔ )
[83]	Альтернативный квадрат ↔		-
Чешуевидный	Курносый порядок-4 квадрата		-
Неоднородный			-
Неоднородный			-
[153]	( ↔ ) = ( ↔ )
Неоднородный	Курносый квадрат ↔ ↔	(3.3.4.3.4)	(3.3.3)	(3.3.4.3.4)	(3.3.4.3.4)	+ (3.3.3)

[6,3 ^1,1 ] семья

Существует 11 форм (и только 4, не принадлежащих семейству [6,3,4]), порожденных кольцевыми перестановками группы Коксетера : [6,3 ^1,1 ] или .

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)				Вершинная фигура	Картина
		0	1	0'	3
87	чередующийся порядок-6 куб. ↔	-	-	(∞) (3.3.3.3.3)	(∞) (3.3.3)	(3.6.3.6)
88	кантический порядок-6 куб. ↔	(1) (3.6.3.6)	-	(2) (6.6.6)	(2) (3.6.6)
89	рунич порядка-6 куб. ↔	(1) (6.6.6)	-	(3) (3.4.6.4)	(1) (3.3.3)
90	ранцикантический порядок-6 куб. ↔	(1) (3.12.12)	-	(2) (4.6.12)	(1) (3.6.6)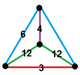
[16]	шестиугольный порядка 4 ↔	(4) (6.6.6)	-	(4) (6.6.6)	-	(3.3.3.3)
[17]	выпрямленный порядка 4 шестиугольный ↔	(2) (3.6.3.6)	-	(2) (3.6.3.6)	(2) (3.3.3.3)
[18]	ректифицированный заказ-6 куб. ↔	(1) (3.3.3.3.3)	-	(1) (3.3.3.3.3)	(6) (3.4.3.4)
[20]	усеченный шестиугольный порядка 4 ↔	(2) (3.12.12)	-	(2) (3.12.12)	(1) (3.3.3.3)
[21]	битусеченный порядка 6 кубических ↔	(1) (6.6.6)	-	(1) (6.6.6)	(2) (4.6.6)
[24]	согнутого порядка-6 куб. ↔	(1) (3.4.6.4)	(2) (4.4.4)	(1) (3.4.6.4)	(1) (3.4.3.4)
[27]	кантиусеченный порядка 6 куб. ↔	(1) (4.6.12)	(1) (4.4.4)	(1) (4.6.12)	(1) (4.6.6)

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)					Вершинная фигура	Картина
		0	1	0'	3	Все
[141]	чередующийся шестиугольный порядок 4 ↔ ↔ ↔						(4.6.6)
Неоднородный	шестигранный биснуб порядка 4 ↔
Неоднородный	коротконосый выпрямленный шестигранный порядка 4 ↔	(3.3.3.3.6)	(3.3.3)	(3.3.3.3.6)	(3.3.3.3.3)	+ (3.3.3)

Циклические графики

[(4,4,3,3)] семейство

Существует 11 форм, 4 из которых уникальны для этого семейства, порожденных кольцевыми перестановками группы Коксетера : , с ↔ .

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению				Вершинная фигура	Картина
		0	1	2	3
91	тетраэдр-квадрат	-	(6) (444)	(8) (333)	(12) (3434)	(3444)
92	циклическиусеченный квадрат-тетраэдр	(444)	(488)	(333)	(388)
93	циклическиусеченный тетраэдр-квадрат	(1) (3333)	(1) (444)	(4) (366)	(4) (466)
94	усеченный тетраэдр-квадрат	(1) (3444)	(1) (488)	(1) (366)	(2) (468)
[64]	( ↔ ) = выпрямленный октаэдрический порядка 4	(3434)	(4444)	(3434)	(3434)
[65]	( ↔ ) = октаэдрический порядок-4	(3333)	-	(3333)	(3333)
[67]	( ↔ ) = усеченный октаэдр порядка 4	(466)	(4444)	(3434)	(466)
[83]	чередующийся квадрат ( ↔ ) =	(444)	(4444)	-	(444)	(4.3.4.3)
[84]	Кантическая площадь ( ↔ ) =	(388)	(488)	(3434)	(388)
[85]	Рунчичская площадь ( ↔ ) =	(3444)	(3434)	(3333)	(3444)
[86]	рунический квадрат ( ↔ ) =	(468)	(488)	(466)	(468)

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению					Вершинная фигура	Картина
		0	1	2	3	Все
Чешуевидный	курносый порядок-4 октаэдрический = =		-	-		ирр. {}v{4}
Неоднородный
155	чередующийся тетраэдр-квадрат ↔					г{4,3}

[(4,4,4,3)] семейство

Существует 9 форм, порожденных кольцевыми перестановками группы Кокстера : .

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)				Вершинная фигура	Картина
		0	1	2	3
95	кубический квадрат	(8) (4.4.4)	-	(6) (4.4.4.4)	(12) (4.4.4.4)	(3.4.4.4)
96	октаэдр-квадрат	(3.4.3.4)	(3.3.3.3)	-	(4.4.4.4)	(4.4.4.4)
97	циклически усеченный кубический квадрат	(4) (3.8.8)	(1) (3.3.3.3)	(1) (4.4.4.4)	(4) (4.8.8)
98	циклическиусеченный квадратно-кубический	(1) (4.4.4)	(1) (4.4.4)	(3) (4.8.8)	(3) (4.8.8)
99	циклическиусеченный октаэдр-квадрат	(4) (4.6.6)	(4) (4.6.6)	(1) (4.4.4.4)	(1) (4.4.4.4)
100	выпрямленный кубический квадрат	(1) (3.4.3.4)	(2) (3.4.4.4)	(1) (4.4.4.4)	(2) (4.4.4.4)
101	усеченный кубический квадрат	(1) (4.8.8)	(1) (3.4.4.4)	(2) (4.8.8)	(1) (4.8.8)
102	усеченный октаэдр-квадрат	(2) (4.6.8	(1) (4.6.6)	(1) (4.4.4.4)	(1) (4.8.8)
103	всеусеченный октаэдр-квадрат	(1) (4.6.8)	(1) (4.6.8)	(1) (4.8.8)	(1) (4.8.8)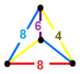

Альтернативные формы

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)					Вершинная фигура
		0	1	2	3	Все
156	чередующийся кубический квадрат ↔	-				(3.4.4.4)
Неоднородный	курносый октаэдр-квадрат
Неоднородный	циклоснуб квадратно-кубический
Неоднородный	циклоснуб октаэдр-квадрат
Неоднородный	омниснуб кубический квадрат	(3.3.3.3.4)	(3.3.3.3.4)	(3.3.4.3.4)	(3.3.4.3.4)	+ (3.3.3)

[(4,4,4,4)] семейство

Существует 5 форм, 1 уникальная, порожденных кольцевыми перестановками группы Коксетера : . Повторяющиеся конструкции связаны как: ↔ , ↔ , и ↔ .

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)				Вершинная фигура	Картина
		0	1	2	3
104	порядок четверти-4 квадрата ↔	(4.8.8)	(4.4.4.4)	(4.4.4.4)	(4.8.8)
[62]	квадрат ↔ ↔	(4.4.4.4)	(4.4.4.4)	(4.4.4.4)	(4.4.4.4)
[77]	порядок-4 квадрата ( ↔ ) =	(4.4.4.4)	-	(4.4.4.4)	(4.4.4.4)	(4.4.4.4)
[78]	усеченный квадрат порядка 4 ( ↔ ) =	(4.8.8)	(4.4.4.4)	(4.8.8)	(4.8.8)
[79]	усеченный квадрат порядка 4 ↔	(4.8.8)	(4.8.8)	(4.8.8)	(4.8.8)

Альтернативные формы

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)					Вершинная фигура
		0	1	2	3	Все
[83]	чередующийся квадрат ( ↔ ↔ ) =	(6) (4.4.4.4)	(6) (4.4.4.4)	(6) (4.4.4.4)	(6) (4.4.4.4)	(8) (4.4.4)	(4.3.4.3)
[77]	чередующийся квадрат четвертого порядка ↔		-
Несимплектический	Кантический порядок-4 квадрата ↔
Неоднородный	циклоснуб квадратный
Неоднородный	курносый порядок-4 квадрат
Неоднородный	биснуб порядка-4 квадрата ↔	(3.3.4.3.4)	(3.3.4.3.4)	(3.3.4.3.4)	(3.3.4.3.4)	+ (3.3.3)

[(6,3,3,3)] семейство

Существует 9 форм, порожденных кольцевыми перестановками группы Кокстера : .

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)				Вершинная фигура
		0	1	2	3
105	тетраэдрально-шестиугольный	(4) (3.3.3)	-	(4) (6.6.6)	(6) (3.6.3.6)	(3.4.3.4)
106	тетраэдрически-треугольный	(3.3.3.3)	(3.3.3)	-	(3.3.3.3.3.3)	(3.4.6.4)
107	циклическиусеченный тетраэдр-шестиугольный	(3) (3.6.6)	(1) (3.3.3)	(1) (6.6.6)	(3) (6.6.6)
108	циклическиусеченный шестиугольно-тетраэдрический	(1) (3.3.3)	(1) (3.3.3)	(4) (3.12.12)	(4) (3.12.12)
109	циклическиусеченный тетраэдрически-треугольный	(6) (3.6.6)	(6) (3.6.6)	(1) (3.3.3.3.3.3)	(1) (3.3.3.3.3.3)
110	выпрямленный тетраэдр-шестиугольный	(1) (3.3.3.3)	(2) (3.4.3.4)	(1) (3.6.3.6)	(2) (3.4.6.4)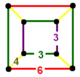
111	усеченный тетраэдр-шестиугольный	(1) (3.6.6)	(1) (3.4.3.4)	(1) (3.12.12)	(2) (4.6.12)
112	усеченный четырехгранно-треугольный	(2) (4.6.6)	(1) (3.6.6)	(1) (3.4.6.4)	(1) (6.6.6)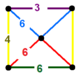
113	всеусеченный тетраэдр-шестиугольный	(1) (4.6.6)	(1) (4.6.6)	(1) (4.6.12)	(1) (4.6.12)

Альтернативные формы

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)					Вершинная фигура
		0	1	2	3	Все
Неоднородный	омниснуб тетраэдрически-шестиугольный	(3.3.3.3.3)	(3.3.3.3.3)	(3.3.3.3.6)	(3.3.3.3.6)	+ (3.3.3)

[(6,3,4,3)] семейство

Существует 9 форм, порожденных кольцевыми перестановками группы Кокстера :

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)				Вершинная фигура
		0	1	2	3
114	октаэдрически-шестиугольный	(6) (3.3.3.3)	-	(8) (6.6.6)	(12) (3.6.3.6)
115	кубически-треугольный	(∞) (3.4.3.4)	(∞) (4.4.4)	-	(∞) (3.3.3.3.3.3)	(3.4.6.4)
116	циклическиусеченный октаэдрически-шестиугольный	(3) (4.6.6)	(1) (4.4.4)	(1) (6.6.6)	(3) (6.6.6)
117	циклоусеченный шестиугольно-октаэдрический	(1) (3.3.3.3)	(1) (3.3.3.3)	(4) (3.12.12)	(4) (3.12.12)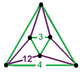
118	циклическиусеченный кубически-треугольный	(6) (3.8.8)	(6) (3.8.8)	(1) (3.3.3.3.3.3)	(1) (3.3.3.3.3.3)
119	выпрямленный октаэдр-шестиугольный	(1) (3.4.3.4)	(2) (3.4.4.4)	(1) (3.6.3.6)	(2) (3.4.6.4)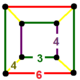
120	усеченный октаэдр-шестиугольник	(1) (4.6.6)	(1) (3.4.4.4)	(1) (3.12.12)	(2) (4.6.12)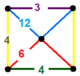
121	усеченный кубо-треугольный	(2) (4.6.8)	(1) (3.8.8)	(1) (3.4.6.4)	(1) (6.6.6)
122	всеусеченный октаэдр-шестиугольный	(1) (4.6.8)	(1) (4.6.8)	(1) (4.6.12)	(1) (4.6.12)

Альтернативные формы

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)					Вершинная фигура
		0	1	2	3	Все
Неоднородный	циклоснуб октаэдрически-шестиугольный	(3.3.3.3.3)	(3.3.3)	(3.3.3.3.3.3)	(3.3.3.3.3.3)	ирр. {3,4}
Неоднородный	омниснуб октаэдрически-шестиугольный	(3.3.3.3.4)	(3.3.3.3.4)	(3.3.3.3.6)	(3.3.3.3.6)	ирр. {3,3}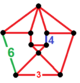

[(6,3,5,3)] семейство

Существует 9 форм, порожденных кольцевыми перестановками группы Кокстера :

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)				Вершинная фигура	Картина
		0	1	2	3
123	икосаэдрально-шестиугольный	(6) (3.3.3.3.3)	-	(8) (6.6.6)	(12) (3.6.3.6)	3.4.5.4
124	додекаэдрально-треугольный	(30) (3.5.3.5)	(20) (5.5.5)	-	(12) (3.3.3.3.3.3)	(3.4.6.4)
125	циклическиусеченный икосаэдр-гексагональный	(3) (5.6.6)	(1) (5.5.5)	(1) (6.6.6)	(3) (6.6.6)
126	циклическиусеченный шестиугольно-икосаэдрический	(1) (3.3.3.3.3)	(1) (3.3.3.3.3)	(5) (3.12.12)	(5) (3.12.12)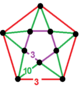
127	циклическиусеченный додекаэдрально-треугольный	(6) (3.10.10)	(6) (3.10.10)	(1) (3.3.3.3.3.3)	(1) (3.3.3.3.3.3)
128	выпрямленный икосаэдр-шестиугольный	(1) (3.5.3.5)	(2) (3.4.5.4)	(1) (3.6.3.6)	(2) (3.4.6.4)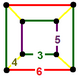
129	усеченный икосаэдр-шестиугольный	(1) (5.6.6)	(1) (3.5.5.5)	(1) (3.12.12)	(2) (4.6.12)
130	усеченный додекаэдр-треугольный	(2) (4.6.10)	(1) (3.10.10)	(1) (3.4.6.4)	(1) (6.6.6)
131	всеусеченный икосаэдр-шестиугольный	(1) (4.6.10)	(1) (4.6.10)	(1) (4.6.12)	(1) (4.6.12)

Альтернативные формы

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)					Вершинная фигура	Картина
		0	1	2	3	Все
Неоднородный	omnisnub икосаэдр-шестиугольный	(3.3.3.3.5)	(3.3.3.3.5)	(3.3.3.3.6)	(3.3.3.3.6)	+ (3.3.3)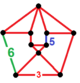

[(6,3,6,3)] семейство

Существует 6 форм, порожденных кольцевыми перестановками группы Кокстера : .

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)				Вершинная фигура	Картина
		0	1	2	3
132	шестиугольно-треугольный	(3.3.3.3.3.3)	-	(6.6.6)	(3.6.3.6)	(3.4.6.4)
133	циклическиусеченный шестиугольно-треугольный	(1) (3.3.3.3.3.3)	(1) (3.3.3.3.3.3)	(3) (3.12.12)	(3) (3.12.12)
134	циклическиусеченный треугольно-шестиугольный	(1) (3.6.3.6)	(2) (3.4.6.4)	(1) (3.6.3.6)	(2) (3.4.6.4)
135	выпрямленный шестиугольно-треугольный	(1) (6.6.6)	(1) (3.4.6.4)	(1) (3.12.12)	(2) (4.6.12)
136	усеченный шестиугольно-треугольный	(1) (4.6.12)	(1) (4.6.12)	(1) (4.6.12)	(1) (4.6.12)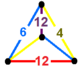
[16]	Шестиугольная плитка порядка 4 =	(3) (6.6.6)	(1) (6.6.6)	(1) (6.6.6)	(3) (6.6.6)	(3.3.3.3)

Альтернативные формы

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)					Вершинная фигура	Картина
		0	1	2	3	Все
[141]	чередующийся шестиугольный порядок 4 ↔ ↔ ↔	(3.3.3.3.3.3)	(3.3.3.3.3.3)	(3.3.3.3.3.3)	(3.3.3.3.3.3)	+ (3.3.3.3)	(4.6.6)
Неоднородный	циклокантиснуб шестиугольно-треугольный
Неоднородный	циклорунцикантиснуб шестиугольно-треугольный
Неоднородный	курносый выпрямленный шестиугольно-треугольный	(3.3.3.3.6)	(3.3.3.3.6)	(3.3.3.3.6)	(3.3.3.3.6)	+ (3.3.3)

Петлевые графики

[3,3 ^[3] ] семья

Существует 11 форм, 4 из которых уникальные, порожденные кольцевыми перестановками группы Коксетера : [3,3 ^[3] ] или . 7 — формы полусимметрии [3,3,6]: ↔ .

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)				вершина фигуры	Картина
		0	1	0'	3
137	чередующийся шестиугольный ( ↔ ) =	-	-	(3.3.3)	(3.3.3.3.3.3)	(3.6.6)
138	Кантик шестиугольный ↔	(1) (3.3.3.3)	-	(2) (3.6.6)	(2) (3.6.3.6)
139	рунчик шестиугольный ↔	(1) (4.4.4)	(1) (4.4.3)	(3) (3.4.3.4)	(1) (3.3.3.3.3.3)
140	рунический шестиугольный ↔	(1) (3.10.10)	(1) (4.4.3)	(2) (4.6.6)	(1) (3.6.3.6)
[2]	выпрямленный шестиугольный ↔	(1) (3.3.3)	-	(1) (3.3.3)	(6) (3.6.3.6)	Треугольная призма
[3]	выпрямленный тетраэдр шестого порядка ↔	(2) (3.3.3.3)	-	(2) (3.3.3.3)	(2) (3.3.3.3.3.3)	Шестиугольная призма
[4]	тетраэдр 6-го порядка ↔	(4) (4.4.4)	-	(4) (4.4.4)	-
[8]	согнутый тетраэдр порядка 6 ↔	(1) (3.3.3.3)	(2) (4.4.6)	(1) (3.3.3.3)	(1) (3.6.3.6)
[9]	усеченный тетраэдр порядка 6 ↔	(1) (3.6.6)	-	(1) (3.6.6)	(2) (6.6.6)
[10]	усеченный тетраэдр шестого порядка ↔	(2) (3.10.10)	-	(2) (3.10.10)	(1) (3.6.3.6)
[14]	усеченный тетраэдр порядка 6 ↔	(1) (4.6.6)	(1) (4.4.6)	(1) (4.6.6)	(1) (6.6.6)

Альтернативные формы

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)					вершина фигуры
		0	1	0'	3	Все
Неоднородный	курносый выпрямленный тетраэдр шестого порядка ↔	(3.3.3.3.3)	(3.3.3.3)	(3.3.3.3.3)	(3.3.3.3.3.3)	+ (3.3.3)

[4,3 ^[3] ] семья

Существует 11 форм, 4 из которых уникальные, порожденные кольцевыми перестановками группы Кокстера : [4,3 ^[3] ] или . 7 — формы полусимметрии [4,3,6]: ↔ .

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)				вершина фигуры	Картина
		0	1	0'	3
141	чередующийся шестиугольный порядок 4 ↔	-	-	(3.3.3.3)	(3.3.3.3.3.3)	(4.6.6)
142	кантический порядок-4 шестиугольный ↔ ↔	(1) (3.4.3.4)	-	(2) (4.6.6)	(2) (3.6.3.6)
143	рунцич порядка 4 шестиугольный ↔	(1) (4.4.4)	(1) (4.4.3)	(3) (3.4.4.4)	(1) (3.3.3.3.3.3)
144	рунцикантический порядок-4 шестиугольный ↔	(1) (3.8.8)	(1) (4.4.3)	(2) (4.6.8)	(1) (3.6.3.6)
[16]	шестиугольный порядка 4 ↔	(4) (4.4.4)	-	(4) (4.4.4)	-
[17]	выпрямленный порядка 4 шестиугольный ↔	(1) (3.3.3.3)	-	(1) (3.3.3.3)	(6) (3.6.3.6)
[18]	ректифицированный заказ-6 куб. ↔	(2) (3.4.3.4)	-	(2) (3.4.3.4)	(2) (3.3.3.3.3.3)
[21]	усеченный шестиугольный порядка 4 ↔	(1) (4.6.6)	-	(1) (4.6.6)	(2) (6.6.6)
[22]	усеченный порядка-6 куб. ↔	(2) (3.8.8)	-	(2) (3.8.8)	(1) (3.6.3.6)
[23]	согнутый 4-го порядка шестиугольный ↔	(1) (3.4.4.4)	(2) (4.4.6)	(1) (3.4.4.4)	(1) (3.6.3.6)
[26]	усеченный шестиугольный порядка 4 ↔	(1) (4.6.8)	(1) (4.4.6)	(1) (4.6.8)	(1) (6.6.6)

Альтернативные формы

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)					вершина фигуры
		0	1	0'	3	Все
Неоднородный	коротконосый выпрямленный шестигранный порядка 4 ↔	(3.3.3.3.4)	(3.3.3.3)	(3.3.3.3.4)	(3.3.3.3.3.3)	+ (3.3.3)

[5,3 ^[3] ] семья

Существует 11 форм, 4 из которых уникальные, порожденные кольцевыми перестановками группы Коксетера : [5,3 ^[3] ] или . 7 — формы полусимметрии [5,3,6]: ↔ .

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)				вершина фигуры	Картина
		0	1	0'	3
145	чередующийся шестиугольный порядок 5 ↔	-	-	(3.3.3.3.3)	(3.3.3.3.3.3)	(3.6.3.6)
146	кантический порядок-5 шестиугольный ↔	(1) (3.5.3.5)	-	(2) (5.6.6)	(2) (3.6.3.6)
147	рунцич порядка 5 шестиугольный ↔	(1) (5.5.5)	(1) (4.4.3)	(3) (3.4.5.4)	(1) (3.3.3.3.3.3)
148	рунцикантический порядок-5 шестиугольный ↔	(1) (3.10.10)	(1) (4.4.3)	(2) (4.6.10)	(1) (3.6.3.6)
[32]	выпрямленный порядка 5 шестиугольный ↔	(1) (3.3.3.3.3)	-	(1) (3.3.3.3.3)	(6) (3.6.3.6)
[33]	исправленный додекаэдр порядка 6 ↔	(2) (3.5.3.5)	-	(2) (3.5.3.5)	(2) (3.3.3.3.3.3)
[34]	Орден-5 шестиугольный ↔	(4) (5.5.5)	-	(4) (5.5.5)	-
[35]	усеченный додекаэдр порядка 6 ↔	(2) (3.10.10)	-	(2) (3.10.10)	(1) (3.6.3.6)
[38]	согнутый 5-го порядка шестиугольный ↔	(1) (3.4.5.4)	(2) (6.4.4)	(1) (3.4.5.4)	(1) (3.6.3.6)
[39]	усеченный шестиугольный порядка 5 ↔	(1) (5.6.6)	-	(1) (5.6.6)	(2) (6.6.6)
[44]	усеченный шестиугольный порядка 5 ↔	(1) (4.6.10)	(1) (6.4.4)	(1) (4.6.10)	(1) (6.6.6)

Альтернативные формы

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)					вершина фигуры	Картина
		0	1	0'	3	Все
Неоднородный	коротконосый выпрямленный шестигранный порядка 5 ↔	(3.3.3.3.5)	(3.3.3)	(3.3.3.3.5)	(3.3.3.3.3.3)	+ (3.3.3)

[6,3 ^[3] ] семья

Существует 11 форм, 4 из которых уникальные, порожденные кольцевыми перестановками группы Коксетера : [6,3 ^[3] ] или . 7 — формы полусимметрии [6,3,6]: ↔ .

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)				вершина фигуры	Картина
		0	1	0'	3
149	рунцич порядка 6 шестиугольный ↔	(1) (6.6.6)	(1) (4.4.3)	(3) (3.4.6.4)	(1) (3.3.3.3.3.3)
150	рунцикантический порядок-6 шестиугольный ↔	(1) (3.12.12)	(1) (4.4.3)	(2) (4.6.12)	(1) (3.6.3.6)
[1]	шестиугольный ↔ ↔ ↔	(1) (6.6.6)	-	(1) (6.6.6)	(2) (6.6.6)
[46]	шестиугольный порядка 6 ↔	(4) (6.6.6)	-	(4) (6.6.6)	-
[47]	выпрямленный шестиугольный порядка 6 ↔	(2) (3.6.3.6)	-	(2) (3.6.3.6)	(2) (3.3.3.3.3.3)
[47]	выпрямленный шестиугольный порядка 6 ↔	(1) (3.3.3.3.3.3)	-	(1) (3.3.3.3.3.3)	(6) (3.6.3.6)
[48]	усеченный шестиугольный порядка 6 ↔	(2) (3.12.12)	-	(2) (3.12.12)	(1) (3.3.3.3.3.3)
[49]	согнутый шестиугольный порядок-6 ↔	(1) (3.4.6.4)	(2) (6.4.4)	(1) (3.4.6.4)	(1) (3.6.3.6)
[51]	усеченный шестиугольный порядка 6 ↔	(1) (4.6.12)	(1) (6.4.4)	(1) (4.6.12)	(1) (6.6.6)
[54]	треугольные соты для плитки ( ↔ ) =	-	-	(3.3.3.3.3.3)	(3.3.3.3.3.3)	(6.6.6)
[55]	Кантический порядок-6 шестиугольный ( ↔ ) =	(1) (3.6.3.6)	-	(2) (6.6.6)	(2) (3.6.3.6)

Альтернативные формы

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)					вершина фигуры	Картина
		0	1	0'	3	Все
[54]	треугольные соты для плитки ( ↔ ↔ ) =		-		-		(6.6.6)
[137]	чередующийся шестиугольный ( ↔ ) = ( ↔ )		-			+ (3.6.6)	(3.6.6)
[47]	выпрямленный шестиугольный порядка 6 ↔ ↔ ↔	(3.6.3.6)	-	(3.6.3.6)	(3.3.3.3.3.3)
[55]	Кантический порядок-6 шестиугольный ( ↔ ) = ( ↔ ) =	(1) (3.6.3.6)	-	(2) (6.6.6)	(2) (3.6.3.6)
Неоднородный	коротконосый выпрямленный шестигранный порядка 6 ↔	(3.3.3.3.6)	(3.3.3.3)	(3.3.3.3.6)	(3.3.3.3.3.3)	+ (3.3.3)

Мультициклические графы

[3 ^{[ ]×[ ]} ] семья

Существует 8 форм, 1 уникальная, порожденных кольцевыми перестановками группы Коксетера : . Два дублируются как ↔ , два как ↔ , и три как ↔ .

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)				Вершинная фигура	Картина
		0	1	2	3
151	Четверть порядка-4 шестиугольная ↔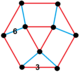
[17]	выпрямленный порядка 4 шестиугольный 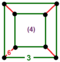↔ ↔ ↔					(4.4.4)
[18]	ректифицированный заказ-6 куб. 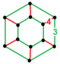↔ ↔ ↔					(6.4.4)
[21]	битусеченный порядка 6 кубических ↔ ↔ ↔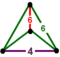
[87]	чередующийся порядок-6 куб. ↔ ↔	-				( 3.6.3.6 )
[88]	кантический порядок-6 куб. ↔ ↔
[141]	чередующийся шестиугольный порядок 4 ↔ ↔		-			( 4.6.6 )
[142]	кантический порядок-4 шестиугольный ↔ ↔

#	Сотовое имя Диаграмма Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)					Вершинная фигура	Картина
		0	1	2	3	Все
Неоднородный	биснуб заказ-6 куб. ↔					ирр. {3,3}

[3 ^[3,3] ] семья

Существует 4 формы, 0 уникальных, порожденных кольцевыми перестановками группы Кокстера : . Они повторяются в четырех семействах: ↔ (индекс 2 подгруппы), ↔ (индекс 4 подгруппы), ↔ (подгруппа индекса 6) и ↔ (индекс 24 подгруппы).

#	Имя Диаграмма Кокстера	0	1	2	3	вершина фигуры	Картина
[1]	шестиугольный ↔					{3,3}
[47]	выпрямленный шестиугольный порядка 6 ↔					т{2,3}
[54]	треугольные соты для плитки ( ↔ ) =		-			т{3 [3] }
[55]	выпрямленный треугольный ↔					т{2,3}

#	Имя Диаграмма Кокстера	0	1	2	3	Все	вершина фигуры	Картина
[137]	чередующийся шестиугольный ( ↔ ) =	с{3 [3] }	с{3 [3] }	с{3 [3] }	с{3 [3] }	{3,3}	(4.6.6)

Сводные перечисления по семействам

Линейные графики

Паракомпактное гиперболическое перечисление

Группа	Расширенный симметрия	Соты		Хиральный расширенный симметрия	Чередование сот
${\bar {R}}_{3}$ [4,4,3]	[4,4,3]	15	| | | | | | | | | | | |	[1 + ,4,1 + ,4,3 + ]	(6)	(↔ ) (↔ ) | |
				[4,4,3] +	(1)
${\bar {N}}_{3}$ [4,4,4]	[4,4,4]	3	| |	[1 + ,4,1 + ,4,1 + ,4,1 + ]	(3)	(↔ = ) |
	[4,4,4] ↔	(3)	| |	[1 + ,4,1 + ,4,1 + ,4,1 + ]	(3)	(↔ ) |
	[2 + [4,4,4]]	3	| |	[2 + [(4,4 + ,4,2 + )]]	(2)	|
				[2 + [4,4,4]] +	(1)
${\bar {V}}_{3}$ [6,3,3]	[6,3,3]	15	| | | | | | | | | | | |	[1 + ,6,(3,3) + ]	(2)	(↔ )
				[6,3,3] +	(1)
${\bar {BV}}_{3}$ [6,3,4]	[6,3,4]	15	| | | | | | | | | | | |	[1 + ,6,3 + ,4,1 + ]	(6)	(↔ ) (↔ ) | |
				[6,3,4] +	(1)
${\bar {HV}}_{3}$ [6,3,5]	[6,3,5]	15	| | | | | | | | | | | |	[1 + ,6,(3,5) + ]	(2)	(↔ )
				[6,3,5] +	(1)
${\bar {Y}}_{3}$ [3,6,3]	[3,6,3]	5	| | | |
	[3,6,3] ↔	(1)		[2 + [3 + ,6,3 + ]]	(1)
	[2 + [3,6,3]]	3	| |	[2 + [3,6,3]] +	(1)
${\bar {Z}}_{3}$ [6,3,6]	[6,3,6]	6	| | | |	[1 + ,6,3 + ,6,1 + ]	(2)	(↔ )
	[2 + [6,3,6]] ↔	(1)		[2 + [(6,3 + ,6,2 + )]]	(2)
	[2 + [6,3,6]]	2	|
				[2 + [6,3,6]] +	(1)

Трезубцы графы

Паракомпактное гиперболическое перечисление

Группа	Расширенный симметрия	Соты		Хиральный расширенный симметрия	Чередование сот
${\bar {DV}}_{3}$ [6,3 1,1 ]	[6,3 1,1 ]	4	| | |
	[1[6,3 1,1 ]]=[6,3,4] ↔	(7)	| | | | | |	[1[1 + ,6,3 1,1 ]] +	(2)	(↔ )
				[1[6,3 1,1 ]] + =[6,3,4] +	(1)
${\bar {O}}_{3}$ [3,4 1,1 ]	[3,4 1,1 ]	4	| | |	[3 + ,4 1,1 ] +	(2)	↔
	[1[3,4 1,1 ]]=[3,4,4] ↔	(7)	| | | | | |	[1[3 + ,4 1,1 ]] +	(2)	|
				[1[3,4 1,1 ]] +	(1)
${\bar {M}}_{3}$ [4 1,1,1 ]	[4 1,1,1 ]	0	(никто)
	[1[4 1,1,1 ]]=[4,4,4] ↔	(4)	| | |	[1[1 + ,4,1 + ,4 1,1 ]] + =[(4,1 + ,4,1 + ,4,2 + )]	(4)	(↔ ) | |
	[3[4 1,1,1 ]]=[4,4,3] ↔	(3)	| |	[3[1 + ,4 1,1,1 ]] + =[1 + ,4,1 + ,4,3 + ]	(2)	(↔ )
				[3[4 1,1,1 ]] + =[4,4,3] +	(1)

Циклические графики

Паракомпактное гиперболическое перечисление

Группа	Расширенный симметрия	Соты		Хиральный расширенный симметрия	Чередование сот
${\widehat {CR}}_{3}$ [(4,4,4,3)]	[(4,4,4,3)]	6	| | | | |	[(4,1 + ,4,1 + ,4,3 + )]	(2)	↔
	[2 + [(4,4,4,3)]]	3	| |	[2 + [(4,4 + ,4,3 + )]]	(2)	|
				[2 + [(4,4,4,3)]] +	(1)
${\widehat {RR}}_{3}$ [4 [4] ]	[4 [4] ]	(никто)
	[2 + [4 [4] ]]	1		[2 + [(4 + ,4) [2] ]]	(1)
	[1[4 [4] ]]=[4,4 1,1 ] ↔	(2)		[(1 + ,4) [4] ]	(2)	↔
	[2[4 [4] ]]=[4,4,4] ↔	(1)		[2 + [(1 + ,4,4) [2] ]]	(1)
	[(2 + ,4)[4 [4] ]]=[2 + [4,4,4]] =	(1)		[(2 + ,4)[4 [4] ]] + = [2 + [4,4,4]] +	(1)
${\widehat {AV}}_{3}$ [(6,3,3,3)]	[(6,3,3,3)]	6	| | | | |
	[2 + [(6,3,3,3)]]	3	| |	[2 + [(6,3,3,3)]] +	(1)
${\widehat {BV}}_{3}$ [(3,4,3,6)]	[(3,4,3,6)]	6	| | | | |	[(3 + ,4,3 + ,6)]	(1)
	[2 + [(3,4,3,6)]]	3	| |	[2 + [(3,4,3,6)]] +	(1)
${\widehat {HV}}_{3}$ [(3,5,3,6)]	[(3,5,3,6)]	6	| | | | |
	[2 + [(3,5,3,6)]]	3	| |	[2 + [(3,5,3,6)]] +	(1)
${\widehat {VV}}_{3}$ [(3,6) [2] ]	[(3,6) [2] ]	2	|
	[2 + [(3,6) [2] ]]	1
	[2 + [(3,6) [2] ]]	1
	[2 + [(3,6) [2] ]] =	(1)		[2 + [(3 + ,6) [2] ]]	(1)
	[(2,2) + [(3,6) [2] ]]	1		[(2,2) + [(3,6) [2] ]] +	(1)

Паракомпактное гиперболическое перечисление

Группа	Расширенный симметрия	Соты		Хиральный расширенный симметрия	Чередование сот
${\widehat {BR}}_{3}$ [(3,3,4,4)]	[(3,3,4,4)]	4	| | |
	[1[(4,4,3,3)]]=[3,4 1,1 ] ↔	(7)	| | | | | |	[1[(3,3,4,1 + ,4)]] + = [3 + ,4 1,1 ] +	(2)	(= )
				[1[(3,3,4,4)]] + = [3,4 1,1 ] +	(1)
${\bar {DP}}_{3}$ [3 [ ]x[ ] ]	[3 [ ]x[ ] ]	1
	[1[3 [ ]x[ ] ]]=[6,3 1,1 ] ↔	(2)	|
	[1[3 [ ]x[ ] ]]=[4,3 [3] ] ↔	(2)	|
	[2[3 [ ]x[ ] ]]=[6,3,4] ↔	(3)	| |	[2[3 [ ]x[ ] ]] + =[6,3,4] +	(1)
${\bar {PP}}_{3}$ [3 [3,3] ]	[3 [3,3] ]	0	(никто)
	[1[3 [3,3] ]]=[6,3 [3] ] ↔	0	(никто)
	[3[3 [3,3] ]]=[3,6,3] ↔	(2)	|
	[2[3 [3,3] ]]=[6,3,6] ↔	(1)
	[(3,3)[3 [3,3] ]]=[6,3,3] =	(1)		[(3,3)[3 [3,3] ]] + = [6,3,3] +	(1)

Петлевые графики

Симметрию в этих графах можно удвоить, добавив зеркало: [1[ n ,3 ^[3] ]] = [ п ,3,6]. Поэтому графы кольцевой симметрии повторяются в семействах линейных графов.

Паракомпактное гиперболическое перечисление

Группа	Расширенный симметрия	Соты		Хиральный расширенный симметрия	Чередование сот
${\bar {P}}_{3}$ [3,3 [3] ]	[3,3 [3] ]	4	| | |
	[1[3,3 [3] ]]=[3,3,6] ↔	(7)	| | | | | |	[1[3,3 [3] ]] + = [3,3,6] +	(1)
${\bar {BP}}_{3}$ [4,3 [3] ]	[4,3 [3] ]	4	| | |
	[1[4,3 [3] ]]=[4,3,6] ↔	(7)	| | | | | |	[1 + ,4,(3 [3] ) + ]	(2)	↔
				[4,3 [3] ] +	(1)
${\bar {HP}}_{3}$ [5,3 [3] ]	[5,3 [3] ]	4	| | |
	[1[5,3 [3] ]]=[5,3,6] ↔	(7)	| | | | | |	[1[5,3 [3] ]] + = [5,3,6] +	(1)
${\bar {VP}}_{3}$ [6,3 [3] ]	[6,3 [3] ]	2	|
	[6,3 [3] ] =	(2)	( ↔ ) | ( = )
	[(3,3)[1 + ,6,3 [3] ]]=[6,3,3] ↔ ↔	(1)		[(3,3)[1 + ,6,3 [3] ]] +	(1)
	[1[6,3 [3] ]]=[6,3,6] ↔	(6)	| | | | |	[3[1 + ,6,3 [3] ]] + = [3,6,3] +	(1)	↔ (= )
				[1[6,3 [3] ]] + = [6,3,6] +	(1)

См. также

• Равномерные мозаики в гиперболической плоскости
• Список правильных многогранников # Тесселяции гиперболического трехмерного пространства

Ссылки

• Джеймс Э. Хамфрис , Группы отражения и группы Кокстера , Кембриджские исследования по высшей математике, 29 (1990)
• Красота геометрии: двенадцать эссе (1999), Dover Publications, LCCN   99-35678 , ISBN   0-486-40919-8 (Глава 10, Обычные соты в гиперболическом пространстве , заархивировано 10 июня 2016 г. в Wayback Machine )
• Коксетер , Правильные многогранники , 3-е. изд., Dover Publications, 1973. ISBN   0-486-61480-8 . (Таблицы I и II: Правильные многогранники и соты, стр. 294–296)
• Джеффри Р. Уикс. Форма пространства, 2-е издание ISBN   0-8247-0709-5 (Глава 16-17: Геометрии трехмерных многообразий I, II)
• Разложения Кокстера гиперболических тетраэдров , arXiv / PDF , А. Феликсон, декабрь 2002 г.
• К.В.Л. Гарнер, Правильные косые многогранники в гиперболической трехмерной банке. Дж. Математика. 19, 1179–1186, 1967. PDF [1] Архивировано 2 апреля 2015 г. в Wayback Machine.
• Норман Джонсон , Геометрии и трансформации , (2018) Главы 11,12,13
• Н. В. Джонсон, Р. Келлерхалс , Дж. Г. Рэтклифф, С. Т. Чанц, Размер гиперболического симплекса Кокстера , Группы преобразований (1999), Том 4, Выпуск 4, стр. 329–353 [2] [3]
• Н. В. Джонсон, Р. Келлерхалс , Дж. Г. Рэтклифф, С. Т. Чанц, Классы соизмеримости гиперболических групп Кокстера , (2002) H ³ :стр130. [4]
• Клитцинг, Ричард. «Гиперболические соты Н3 паракомпакт» .