Треугольные соты для плитки

Треугольные соты для плитки

Тип	Гиперболические обычные соты Паракомпактный однородный сотовый
Символ Шлефли	{3,6,3} ч{6,3,6} ч{6,3 ^[3]} ↔ {3 ^[3,3]}
Диаграммы Кокстера-Динкина	↔ ↔ ↔
Клетки	{3,6}
Лица	треугольник {3}
Краевая фигура	треугольник {3}
Вершинная фигура	шестиугольная плитка
Двойной	Самодвойственный
Группы Кокстера	${\overline {Y}}_{3}$ , [3,6,3] ${\overline {VP}}_{3}$ , [6,3 ^[3]] ${\overline {PP}}_{3}$ , [3 ^[3,3]]
Характеристики	Обычный

Треугольные мозаичные соты — одна из 11 паракомпактных регулярных мозаик, заполняющих пространство (или сот ) в гиперболическом трёхмерном пространстве . Его называют паракомпактным, потому что он имеет бесконечные ячейки и фигуры вершин , причем все вершины представляют собой идеальные точки, удаленные на бесконечность. Он имеет символ Шлефли {3,6,3}, состоящий из треугольных ячеек мозаики. Каждый край сот окружен тремя ячейками, а каждая вершина является идеальной, поскольку в ней встречается бесконечное количество ячеек. Его вершинная фигура представляет собой шестиугольную мозаику .

Геометрические соты — это заполнение пространства многогранными ячейками более высокой размерности или ячейками , чтобы не было пробелов. Это пример более общего математического разбиения или мозаики в любом количестве измерений.

Соты обычно строятся в обычном евклидовом («плоском») пространстве, как и выпуклые однородные соты . Они также могут быть построены в неевклидовых пространствах , таких как гиперболические однородные соты . Любой конечный однородный многогранник можно спроецировать на его описанную сферу, чтобы сформировать однородную соту в сферическом пространстве.

Симметрия

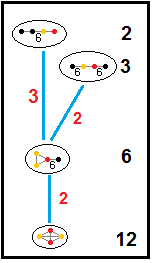
Он имеет две конструкции с более низкой отражающей симметрией, представляющие собой чередующиеся соты шестиугольной плитки шестого порядка . ↔ , и как от , который чередует 3 типа (цвета) треугольных мозаик вокруг каждого ребра. В обозначениях Кокстера удаление 3-го и 4-го зеркал, [3,6,3 ^*] создает новую группу Кокстера [3 ^[3,3]], , индекс подгруппы 6. Фундаментальная область в 6 раз больше. Согласно диаграмме Кокстера, в новой фундаментальной области имеется три копии первого исходного зеркала: ↔ .

Связанные плитки

Он похож на двумерную гиперболическую апейрогональную мозаику бесконечного порядка {∞, ∞} с бесконечными апейрогональными гранями и со всеми вершинами на идеальной поверхности.

Связанные соты

Треугольные мозаичные соты представляют собой обычные гиперболические соты в трехмерном пространстве и одну из одиннадцати паракомпактных сот.

11 паракомпактных стандартных сот
{6,3,3}	{6,3,4}	{6,3,5}	{6,3,6}	{4,4,3}	{4,4,4}
{3,3,6}	{4,3,6}	{5,3,6}	{3,6,3}	{3,4,4}

имеется девять однородных сот [3,6,3] В семействе групп Кокстера , включая эту правильную форму, а также усеченную форму t _1,2 {3,6,3}, со всеми усеченными гранями шестиугольной мозаики .

[3,6,3] семейные соты
{3,6,3}	г {3,6,3}	т{3,6,3}	рр{3,6,3}	т _0,3 {3,6,3}	2т{3,6,3}	тр{3,6,3}	т _0,1,3 {3,6,3}	т _0,1,2,3 {3,6,3}

Соты также входят в серию полихор и сот с треугольными краями .

{3, p , 3} многогранники
Space	S³		H³
Form	Finite		Compact	Paracompact	Noncompact
{3,p,3}	{3,3,3}	{3,4,3}	{3,5,3}	{3,6,3}	{3,7,3}	{3,8,3}	... {3,∞,3}
Image
Cells	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}
Vertex figure	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

Ректифицированные треугольные соты для плитки

Ректифицированные треугольные соты для плитки
Тип	Паракомпактный однородный сотовый
Символ Шлефли	г {3,6,3} ч ₂ {6,3,6}
Диаграмма Кокстера	↔ ↔ ↔
Клетки	г{3,6} {6,3}
Лица	треугольник {3} шестигранник {6}
Вершинная фигура	треугольная призма
Группа Коксетера	${\overline {Y}}_{3}$ , [3,6,3] ${\overline {VP}}_{3}$ , [6,3 ^[3]] ${\overline {PP}}_{3}$ , [3 ^[3,3]]
Характеристики	Вершинно-транзитивный, реберно-транзитивный

Ректифицированные треугольные соты для черепицы , , имеет тригексагональную мозаику и шестиугольные ячейки мозаики с треугольной фигурой вершины призмы.

Симметрия

Более низкую симметрию этой соты можно построить как соты с шестиугольной мозаикой кантического порядка 6 . ↔ . Вторая конструкция с меньшим индексом ↔ .

Усеченные треугольные соты для плитки

Усеченные треугольные соты для плитки
Тип	Паракомпактный однородный сотовый
Символ Шлефли	т{3,6,3}
Диаграмма Кокстера
Клетки	т{3,6} {6,3}
Лица	шестигранник {6}
Вершинная фигура	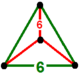тетраэдр
Группа Коксетера	${\overline {Y}}_{3}$ , [3,6,3] ${\overline {V}}_{3}$ , [3,3,6]
Характеристики	Обычный

Усеченные треугольные черепичные соты , , представляет собой форму с более низкой симметрией шестиугольной черепичной соты , . Он содержит шестиугольные грани мозаики с тетраэдрической вершинной фигурой.

Разрезанные треугольные соты для плитки

Разрезанные треугольные соты для плитки
Тип	Паракомпактный однородный сотовый
Символ Шлефли	2т{3,6,3}
Диаграмма Кокстера
Клетки	т{6,3}
Лица	треугольник {3} двенадцатиугольник {12}
Вершинная фигура	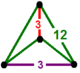тетрагональный дисфеноид
Группа Коксетера	$2\times {\overline {Y}}_{3}$ , [[3,6,3]]
Характеристики	Вершинно-транзитивный, реберно-транзитивный, клеточно-транзитивный

Разрезанные треугольные соты черепицы , , имеет усеченные шестиугольные ячейки мозаики с тетрагональной фигурой вершины дисфеноида .

Скошенные треугольные соты для плитки

Скошенные треугольные соты для плитки
Тип	Паракомпактный однородный сотовый
Символ Шлефли	рр{3,6,3} или т _0,2 {3,6,3} с2 _{ 3,6,3}
Диаграмма Кокстера
Клетки	рр{6,3} г{6,3} {}×{3}
Лица	треугольник {3} квадрат {4} шестигранник {6}
Вершинная фигура	клин
Группа Коксетера	${\overline {Y}}_{3}$ , [3,6,3]
Характеристики	Вершинно-транзитивный

Зубчатые треугольные соты черепицы , , имеет ромбитригексагональную мозаику , тригексагональную мозаику и ячейки треугольной призмы с фигурой вершины клина .

Симметрия

Его также можно сконструировать в виде курносых треугольных сот из черепицы . , полусимметричная форма с симметрией [3 ⁺,6,3].

Скошенные треугольные соты для плитки

Скошенные треугольные соты для плитки
Тип	Паракомпактный однородный сотовый
Символ Шлефли	tr{3,6,3} или t _0,1,2 {3,6,3}
Диаграмма Кокстера
Клетки	тр{6,3} т{6,3} {}×{3}
Лица	треугольник {3} квадрат {4} шестигранник {6} двенадцатиугольник {12}
Вершинная фигура	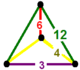зеркальная клиновидная кость
Группа Коксетера	${\overline {Y}}_{3}$ , [3,6,3]
Характеристики	Вершинно-транзитивный

Скошенные треугольные соты черепицы , , имеет усеченную тригексагональную мозаику , усеченную шестиугольную мозаику и треугольные призматические ячейки с зеркальной фигурой клиновидной вершины.

Стержневые треугольные соты для плитки

Стержневые треугольные соты для плитки
Тип	Паракомпактный однородный сотовый
Символ Шлефли	т _0,3 {3,6,3}
Диаграмма Кокстера
Клетки	{3,6} {}×{3}
Лица	треугольник {3} квадрат {4}
Вершинная фигура	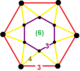шестиугольная антипризма
Группа Коксетера	$2\times {\overline {Y}}_{3}$ , [[3,6,3]]
Характеристики	Вершинно-транзитивный, реберно-транзитивный

Стертые треугольные соты черепицы , , имеет треугольную мозаику и треугольные призматические ячейки с шестиугольной вершиной антипризмы .

Соты из рыхлых усеченных треугольных плиток

Соты из рыхлых усеченных треугольных плиток
Тип	Паракомпактный однородный сотовый
Символы Шлефли	т _0,1,3 {3,6,3} с _2,3 {3,6,3}
Диаграммы Кокстера
Клетки	т{3,6} рр{3,6} {}×{3} {}×{6}
Лица	треугольник {3} квадрат {4} шестигранник {6}
Вершинная фигура	равнобедренно-трапециевидная пирамида
Группа Коксетера	${\overline {Y}}_{3}$ , [3,6,3]
Характеристики	Вершинно-транзитивный

Усеченные треугольные соты черепицы , , имеет шестиугольную мозаику , ромбитригексагональную мозаику , треугольную призму и ячейки шестиугольной призмы с равнобедренно-трапециевидной пирамиды фигурой вершины .

Симметрия

Его также можно сконструировать в виде курносых треугольных сот из черепицы . , полусимметричная форма с симметрией [3 ⁺,6,3].

Всеусеченные треугольные соты для плитки

Всеусеченные треугольные соты для плитки
Тип	Паракомпактный однородный сотовый
Символ Шлефли	т _0,1,2,3 {3,6,3}
Диаграмма Кокстера
Клетки	тр{3,6} {}×{6}
Лица	квадрат {4} шестигранник {6} двенадцатиугольник {12}
Вершинная фигура	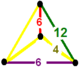филлический дисфеноид
Группа Коксетера	$2\times {\overline {Y}}_{3}$ , [[3,6,3]]
Характеристики	Вершинно-транзитивный, реберно-транзитивный

Всеусеченные треугольные черепичные соты , , имеет усеченную тригексагональную мозаику и ячейки шестиугольной призмы с филлической фигурой дисфеноида в вершине.

Треугольная сотовая плитка Runcisnub

Треугольная сотовая плитка Runcisnub
Тип	Паракомпактные чешуйчатые соты
Символ Шлефли	с ₃ {3,6,3}
Диаграмма Кокстера
Клетки	г{6,3} {}х{3} {3,6} трикуп
Лица	треугольник {3} квадрат {4} шестигранник {6}
Вершинная фигура
Группа Коксетера	${\overline {Y}}_{3}$ , [3 ⁺,6,3]
Характеристики	Вершинно-транзитивный, неоднородный

Треугольные соты Runcisnub для плитки , , имеет тригексагональную черепицу , треугольную черепицу , треугольную призму и купола треугольные ячейки . Он вершинно-транзитивен , но не однороден, так как содержит ячейки Джонсона сплошные треугольные купольные .

См. также

Ссылки

Коксетер , Правильные многогранники , 3-е. изд., Dover Publications, 1973. ISBN 0-486-61480-8 . (Таблицы I и II: Правильные многогранники и соты, стр. 294–296)
Красота геометрии: двенадцать эссе (1999), Dover Publications, LCCN 99-35678 , ISBN 0-486-40919-8 (Глава 10, Правильные соты в гиперболическом пространстве ) Таблица III
Джеффри Р. Уикс. Форма пространства, 2-е издание ISBN 0-8247-0709-5 (Глава 16-17: Геометрии трехмерных многообразий I, II)
Нормана Джонсона Равномерные многогранники , рукопись
- Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.
- Н. В. Джонсон: Геометрии и преобразования , (2018) Глава 13: Гиперболические группы Кокстера