Усеченный ромбокубооктаэдр

Усеченный ромбокубооктаэдр
Символ Шлефли	трр{4,3} = $tr{\begin{Bmatrix}4\\3\end{Bmatrix}}$
Обозначение Конвея	да
Лица	50: 24 {4} 8 {6} 6+12 {8}
Края	144
Вершины	96
Группа симметрии	О h , [4,3], (*432) порядок 48
Группа вращения	О, [4,3] + , (432), порядок 24
Двойной многогранник	Икоситетраэдр Дисдякиса
Характеристики	выпуклый, зоноэдр

— Усеченный ромбокубооктаэдр многогранник , как усечение ромбокубооктаэдра . построенный У него 50 граней, состоящих из 18 восьмиугольников, 8 шестиугольников и 24 квадратов. Он может заполнять пространство усеченным кубом , усеченным тетраэдром и треугольной призмой в виде усеченных рунических кубических сот .

Другие имена

• Усеченный малый ромбокубооктаэдр
• Скошенный кубооктаэдр

Зоноэдр

Как зоноэдр , он может быть построен со всеми восьмиугольниками, кроме 12, как правильные многоугольники . Он имеет два набора по 48 вершин, находящихся на двух расстояниях от его центра.

Он представляет собой Минковского куба сумму , усеченного октаэдра и ромбического додекаэдра .

Раскопанный усеченный ромбокубооктаэдр.

Раскопанный усеченный ромбокубооктаэдр.
Лица	148: 8 {3} 24+96+6 {4} 8 {6} 6 {8}
Края	312
Вершины	144
Эйлерова характеристика	-20
Род	11
Группа симметрии	О h , [4,3], (*432) порядок 48

Раскопанный усеченный ромбокубооктаэдр представляет собой тороидальный многогранник , построенный из усеченного ромбокубооктаэдра с удаленными 12 неправильными восьмиугольными гранями. Он состоит из сети из 6 квадратных куполов , 8 треугольных куполов и 24 треугольных призм . У него 148 граней (8 треугольников, 126 квадратов, 8 шестиугольников и 6 восьмиугольников), 312 ребер и 144 вершины. При эйлеровой характеристике χ = f + v - e = -20 его род (g = (2-χ)/2) равен 11.

Без треугольных призм тороидальный многогранник превращается в усеченный кубооктаэдр.

раскопан

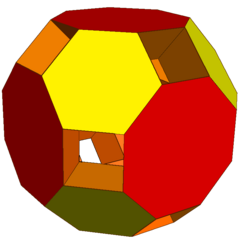Усеченный ромбокубооктаэдр	Усеченный кубооктаэдр

Связанные многогранники

подобен Усеченный кубооктаэдр , со всеми правильными гранями и фигурой вершины 4.6.8 .

Треугольник и квадраты ромбокубооктаэдра можно независимо выпрямлять или усекать, создавая четыре перестановки многогранников. Частично усеченные формы можно рассматривать как сужение краев усеченной формы.

можно Усеченный ромбокубооктаэдр увидеть в последовательности выпрямления и усечения операций кубооктаэдра . Дальнейший шаг чередования приводит к курносому ромбокубооктаэдру .

связанные многогранники

Имя	г{4,3}	рр{4,3}	тр{4,3}	Исправленный ррр{4,3}	Частично усечено		Усечено трр{4,3}	старший CO
Конвей	до нашей эры	ааС=еС	taC=bC	аааC=eaC	dXC	dXdC	тааС=баС	мешок
Изображение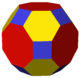
ВертИнжир	3.4.3.4	3.4.4.4	4.6.8	4.4.4. 4 д и 3.4.4 д .4	4.4.4. 6 я и 4.6.6 я	4,6 и .8 и 3.4.6 и .4	4.8. 8 п и 4.6.8 р	3.3.3.3.4 и 3.3.4.3.4

См. также

• Расширенный кубооктаэдр
• Усеченный ромбокосододекаэдр

Ссылки

• Эппштейн, Дэвид (1996). «Зоноэдры и зонотопы» . Математика в образовании и исследованиях . 5 (4): 15–21.
• Кокстера Регулярные многогранники , третье издание, (1973), Дуврское издание, ISBN   0-486-61480-8 (стр. 145–154, глава 8: Усечение)
• Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус , Симметрии вещей 2008, ISBN   978-1-56881-220-5

Внешние ссылки

• Интерпретатор Конвея Джорджа Харта : генерирует многогранники в VRML , принимая в качестве входных данных нотацию Конвея.
• Расширения призмы [1] Модель тороида