Однородный звездчатый многогранник


В геометрии однородный звездчатый многогранник — это самопересекающийся однородный многогранник . Их также иногда называют невыпуклыми многогранниками, подразумевая самопересекающиеся. Каждый многогранник может содержать грани звездчатого многоугольника звездчатого многоугольника , фигуры вершин или и то, и другое.
Полный набор из 57 непризматических однородных звездчатых многогранников включает 4 правильных, называемых многогранниками Кеплера–Пуансо , 14 квазиправильных и 39 полуправильных.
Также существуют два бесконечных набора однородных звездных призм и однородных звездных антипризм .
Так же, как (невырожденные) звездчатые многоугольники ( плотность которых больше 1) соответствуют круговым многоугольникам с перекрывающимися плитками , звездчатые многогранники, которые не проходят через центр, имеют плотность многогранника больше 1 и соответствуют сферическим многогранникам с перекрывающимися плитками; Таких непризматических однородных звездчатых многогранников 47. Остальные 10 непризматических однородных звездчатых многогранников, проходящих через центр, являются полумногогранниками , а также монстром Миллера и не имеют четко определенных плотностей.
Невыпуклые формы строятся из треугольников Шварца .
Все однородные многогранники перечислены ниже по группам симметрии и сгруппированы по расположению вершин.
Правильные многогранники обозначаются их символом Шлефли . Другие неправильные однородные многогранники перечислены с указанием конфигурации их вершин .
Дополнительная фигура, псевдобольшой ромбокубооктаэдр , обычно не включается в состав истинно однородного звездчатого многогранника, несмотря на то, что он состоит из правильных граней и имеет одинаковые вершины.
дополнительный неравномерный Примечание. Для невыпуклых форм ниже используется выпуклой оболочки дескриптор, когда расположение вершин имеет ту же топологию, что и одна из них, но имеет нерегулярные грани. Например, в неоднородной согнутой могут быть созданы прямоугольники форме вместо краев , а не квадраты .
Двугранная симметрия
[ редактировать ]См. Призматический однородный многогранник .
Тетраэдрическая симметрия
[ редактировать ]
Существует одна невыпуклая форма — тетрагемишестиэдр , обладающий тетраэдрической симметрией (с фундаментальной областью треугольника Мёбиуса (3 3 2)).
Существуют два треугольника Шварца , которые порождают уникальные невыпуклые однородные многогранники: один прямоугольный треугольник ( 3 ⁄ 2 3 2) и один общий треугольник ( 3 ⁄ 2 3 3). Общий треугольник ( 3 ⁄ 2 3 3) порождает октагемиоктаэдр , который дается далее с его полной октаэдрической симметрией .
| Расположение вершин ( Выпуклая оболочка ) | Невыпуклые формы | |
|---|---|---|
 Тетраэдр | ||
 Выпрямленный тетраэдр Октаэдр |  4. 3 ⁄ 2 .4.3 3 ⁄ 2 3 | 2 | |
 Усеченный тетраэдр | ||
 Скошенный тетраэдр ( Кубооктаэдр ) | ||
 Всеусеченный тетраэдр ( усеченный октаэдр ) | ||
 Курносый тетраэдр ( Икосаэдр ) | ||
Октаэдрическая симметрия
[ редактировать ]
Существует 8 выпуклых форм и 10 невыпуклых форм с октаэдрической симметрией (с фундаментальной областью треугольника Мёбиуса (4 3 2)).
Имеются четыре треугольника Шварца , порождающие невыпуклые формы, два прямоугольных треугольника ( 3 ⁄ 2 4 2), и ( 4 ⁄ 3 3 2) и два общих треугольника: ( 4 ⁄ 3 4 3), ( 3 ⁄ 2 4 4).
| Расположение вершин ( Выпуклая оболочка ) | Невыпуклые формы | ||
|---|---|---|---|
 Куб | |||
 Октаэдр | |||
 Кубооктаэдр |  6. 4 ⁄ 3 .6.4 4 ⁄ 3 4 | 3 |  6. 3 ⁄ 2 .6.3 3 ⁄ 2 3 | 3 | |
 Усеченный куб |  4. 8 ⁄ 3 . 4 ⁄ 3 . 8 ⁄ 5 2 4 ⁄ 3 ( 3 ⁄ 2 4 ⁄ 2 ) | |  8 ⁄ 3 .3. 8 ⁄ 3 .4 3 4 | 4 ⁄ 3 |  4. 3 ⁄ 2 .4.4 3 ⁄ 2 4 | 2 |
 Усеченный октаэдр | |||
 Ромбокубооктаэдр |  4.8. 4 ⁄ 3 . 8 ⁄ 7 2 4 ( 3 ⁄ 2 4 ⁄ 2 ) | |  8. 3 ⁄ 2 .8.4 3 ⁄ 2 4 | 4 |  8 ⁄ 3 . 8 ⁄ 3 .3 2 3 | 4 ⁄ 3 |
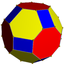 Неоднородный усеченный кубооктаэдр |  4.6. 8 ⁄ 3 2 3 4 ⁄ 3 | | ||
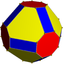 Неоднородный усеченный кубооктаэдр |  8 ⁄ 3 .6.8 3 4 4 ⁄ 3 | | ||
 Курносый куб | |||
Икосаэдрическая симметрия
[ редактировать ]
Существует 8 выпуклых форм и 46 невыпуклых форм с икосаэдрической симметрией (с фундаментальной областью треугольника Мёбиуса (5 3 2)). (или 47 невыпуклых форм, если включить фигуру Скиллинга). Некоторые из невыпуклых курносых форм обладают отражательной вершинной симметрией.
Вырожденные случаи
[ редактировать ]Коксетер методом построения Витхоффа идентифицировал ряд вырожденных звездчатых многогранников, которые содержат перекрывающиеся ребра или вершины. К таким дегенеративным формам относятся:
- Малый сложный икосододекаэдр
- Большой сложный икосододекаэдр
- Малый сложный ромбокосододекаэдр
- Большой сложный ромбокосододекаэдр
- Сложный ромбидодекадодекаэдр
Фигура Скиллинга
[ редактировать ]Еще один невыпуклый вырожденный многогранник — это большой расплющенный диромбидодекаэдр , также известный как фигура Скиллинга , который является однородным по вершинам, но имеет пары ребер, которые совпадают в пространстве, так что четыре грани встречаются на некоторых ребрах. Из-за его двойных ребер он считается вырожденным однородным многогранником, а не однородным многогранником. Он обладает симметрией .
См. также
[ редактировать ]- Звездный многоугольник
- Список однородных многогранников
- Список однородных многогранников по треугольнику Шварца
Ссылки
[ редактировать ]- Коксетер, HSM (13 мая 1954 г.). «Равномерные многогранники». Философские труды Лондонского королевского общества. Серия А, Математические и физические науки . 246 (916): 401–450. дои : 10.1098/rsta.1954.0003 .
- Веннингер, Магнус (1974). Модели многогранников . Издательство Кембриджского университета. ISBN 0-521-09859-9 . OCLC 1738087 .
- Брюкнер М. Многоугольники и многогранники. теория и история. . Лейпциг, Германия: Тойбнер, 1900. [1]
- Сопов С. П. (1970), "Доказательство полноты списка элементарных однородных многогранников", Украинский геометрический сборник (8): 139–156, МР 0326550.
- Скиллинг, Дж. (1975), «Полный набор однородных многогранников», Философские труды Лондонского королевского общества. Серия A. Математические и физические науки , 278 : 111–135, doi : 10.1098/rsta.1975.0022 , ISSN 0080-4614 , JSTOR 74475 , MR 0365333
- Хар'Эл, З. Единообразное решение для однородных многогранников. , Geometriae Dedicata 47, 57-110, 1993. Зви Хар'Эл , программное обеспечение Kaleido , Изображения , двойные изображения
- Мэдер Р.Э. Равномерные многогранники. Mathematica J. 3, 48-57, 1993. [2]
- Мессер, Питер В. Выражения в замкнутой форме для однородных многогранников и их двойников. , Дискретная и вычислительная геометрия 27:353-375 (2002).
- Клитцинг, Ричард. «3D однородные многогранники» .