Хорошо покрытый график

Хорошо покрытый граф — граф пересечений девяти диагоналей шестиугольника . Три красные вершины образуют одно из 14 максимальных независимых множеств одинакового размера, а шесть синих вершин образуют дополнительное минимальное вершинное покрытие.

В теории графов — хорошо покрытый граф это неориентированный граф , в котором все минимальные покрытия вершин имеют одинаковый размер. Здесь вершинное покрытие — это набор вершин, который касается всех ребер, и оно минимально , если удаление из него любой вершины оставит какое-то ребро непокрытым. Аналогично, хорошо покрытые графы — это графы, в которых все максимальные независимые множества имеют одинаковый размер. Хорошо покрытые графы были определены и впервые изучены Майклом Д. Пламмером в 1970 году.

К хорошо покрытым графам относятся все полные графы , сбалансированные полные двудольные графы и ладейные графы , вершины которых представляют собой квадраты шахматной доски, а ребра представляют ходы шахматной ладьи. Известные характеристики хорошо покрытых кубических графов , хорошо покрытых графов без когтей и хорошо покрытых графов большого обхвата позволяют распознавать эти графы за полиномиальное время , но проверка того, хорошо ли покрыты другие типы графов, является coNP. - Полная проблема.

Определения

Вершинное покрытие неориентированного графа — это набор вершин, соприкасающийся с каждым ребром графа. Вершинное покрытие является минимальным или неизбыточным, если удаление любой вершины из него разрушит свойство покрытия: удаление приведет к тому, что какое-то ребро станет непокрытым. Оно минимально, если нет другого вершинного покрытия с меньшим количеством вершин. Хорошо покрытый граф — это граф, в котором каждое минимальное покрытие также является минимальным. В оригинальной статье, определяющей хорошо покрытые графы, Пламмер пишет, что это «очевидно эквивалентно» тому свойству, что каждые два минимальных покрытия имеют одинаковое количество вершин друг у друга.

Независимым множеством в графе называется множество вершин, ни одна из которых не является смежной. Если C графе G , дополнение C является вершинным покрытием в должно быть независимым множеством, и наоборот. C является минимальным вершинным покрытием тогда и только тогда, когда его дополнение I является максимальным независимым множеством, а C является минимальным вершинным покрытием тогда и только тогда, когда его дополнение является максимальным независимым множеством. Следовательно, хорошо покрытый граф — это, эквивалентно, граф, в котором каждое максимальное независимое множество имеет одинаковый размер, или граф, в котором каждое максимальное независимое множество является максимальным.

В исходной статье, определяющей хорошо покрытые графы, эти определения были ограничены связными графами . хотя они имеют смысл и для несвязных графов. Некоторые более поздние авторы заменили требование связности более слабым требованием, согласно которому хорошо покрытый граф не должен иметь изолированных вершин. Как для связных хорошо покрытых графов, так и для хорошо покрытых графов без изолированных вершин не может быть существенных вершин , вершин, которые принадлежат каждому минимальному вершинному покрытию. Кроме того, каждый хорошо покрытый граф является критическим графом для покрытия вершин в том смысле, что для каждой вершины v удаление v из графа дает граф с меньшим минимальным покрытием вершин.

Комплекс независимости графа G — это симплициальный комплекс, симплекс для каждого независимого множества в G. имеющий Симплициальный комплекс называется чистым, если все его максимальные симплексы имеют одинаковую мощность, поэтому хорошо покрытый граф эквивалентно графу с чистым комплексом независимости.

Примеры

	а	б	с	д	и	ж	г	час
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	а	б	с	д	и	ж	г	час

Неатакующее расположение восьми ладей на шахматной доске. Если на шахматной доске расставлено менее восьми ладей не атакующим образом, их всегда можно расширить до восьми ладей, которые остаются не атакующими.

Граф циклов длины четыре или пять хорошо покрыт: в каждом случае каждое максимальное независимое множество имеет размер два. Цикл длины семь и путь длины три также хорошо описаны. Любой полный граф хорошо покрыт: каждое максимальное независимое множество состоит из одной вершины. Аналогично, каждый кластерный граф (несвязное объединение полных графов) хорошо покрыт. Полный двудольный граф является хорошо покрытым, если две стороны его двудольного деления имеют одинаковое число вершин, поскольку это его единственные два максимальных независимых множества. Граф дополнений графа без треугольников и без изолированных вершин хорошо покрыт: он не имеет независимых множеств больше двух, и каждая отдельная вершина может быть расширена до независимого множества с двумя вершинами.

хорошо Граф ладей описан: если разместить любой набор ладей на шахматной доске так, что никакие две ладьи не атакуют друг друга, всегда можно продолжать размещать больше неатакующих ладей до тех пор, пока в каждой строке и столбце не останется по одной. шахматная доска. Граф, вершины которого являются диагоналями простого многоугольника и ребра которого соединяют пары диагоналей, пересекающихся друг с другом, является хорошо покрытым, поскольку его максимальные независимые множества являются триангуляциями многоугольника и все триангуляции имеют одинаковое количество ребер.

Если G — любой n -вершинный граф, то корневое произведение G , каждая из которых с однореберным графом (то есть графом H , образованным добавлением n новых вершин в G имеет степень один и каждая смежна с отдельной вершиной в G ) хорошо покрыт. Действительно, максимальное независимое множество в H должно состоять из произвольного независимого множества в G вместе с соседями дополнительного множества первой степени и, следовательно, должно иметь размер n . В более общем смысле, для любого графа G вместе с кликовым покрытием (разбиением p вершин G на клики) граф G ^п образованный добавлением еще одной вершины к каждой клике с хорошим покрытием; корневое произведение является частным случаем этой конструкции, когда p состоит из n одновершинных клик. Таким образом, каждый граф является индуцированным подграфом хорошо покрытого графа.

Двудольность, очень хорошо покрытые графики и обхват

Фаварон (1982) определяет очень хорошо покрытый граф как хорошо покрытый граф (возможно, несвязный, но без изолированных вершин), в котором каждое максимальное независимое множество (и, следовательно, также каждое минимальное вершинное покрытие) содержит ровно половину вершин. Это определение включает корневые произведения графа G и однореберного графа. Сюда также входят, например, двудольные хорошо покрытые графы, изученные Равиндрой (1977) и Берге (1981) : в двудольном графе без изолированных вершин обе стороны любого двудольного разбиения образуют максимальные независимые множества (и минимальные вершинные покрытия), поэтому если граф хорошо покрыт, обе стороны должны иметь одинаковое количество вершин. В хорошо покрытом графе с n вершинами без изолированных вершин размер максимального независимого множества не превышает n /2 , поэтому очень хорошо покрытые графы — это хорошо покрытые графы, в которых максимальный размер независимого множества максимально велик. .

Двудольный граф G является хорошо покрытым тогда и только тогда, когда он имеет совершенное паросочетание M со свойством, что для каждого ребра uv в M индуцированный подграф соседей u и v образует полный двудольный граф . Характеристика с точки зрения паросочетаний может быть расширена с двудольных графов до очень хорошо покрытых графов: граф G очень хорошо покрыт тогда и только тогда, когда он имеет идеальное паросочетание M со следующими двумя свойствами:

1. Никакое ребро M не принадлежит треугольнику в G и
2. Если ребро M является центральным ребром пути с тремя ребрами в G , то две конечные точки пути должны быть смежными.

Более того, если G очень хорошо покрыта, то каждое совершенное паросочетание в G удовлетворяет этим свойствам.

Деревья являются частным случаем двудольных графов, и проверка того, хорошо ли покрыто дерево, может рассматриваться как гораздо более простой частный случай характеристики хорошо покрытых двудольных графов: если G — дерево с более чем двумя вершинами, оно хорошо покрытым тогда и только тогда, когда каждый нелистовой узел дерева примыкает ровно к одному листу. Та же характеристика применима к графам, которые локально древовидны, в том смысле, что окрестности каждой вершины с малым диаметром являются ациклическими: если граф имеет обхват восемь или более (так что для каждой вершины v подграф вершин на расстоянии три из v ацикличны), то она хорошо покрыта тогда и только тогда, когда каждая вершина степени выше единицы имеет ровно одного соседа степени один. Близко связанная, но более сложная характеристика применима к хорошо покрытым графам обхвата пять и более.

Регулярность и плоскостность

Семь кубических 3-связных хорошо покрытых графов

Кубический 1-связный хорошо покрытый граф, образованный заменой каждого узла шестиузлового пути одним из трех фрагментов.

Курносый дисфеноид , один из четырех хорошо покрытых 4-связных трехмерных симплициальных многогранников.

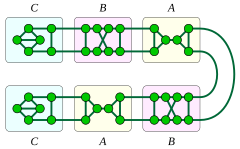
Кубические 3 ( 3-регулярные ) хорошо покрытые графы были классифицированы: они состоят из семи -связных примеров вместе с тремя бесконечными семействами кубических графов с меньшей связностью.

Семь 3-связных кубических хорошо покрытых графов — это полный граф К ₄ , графы треугольной призмы и пятиугольной призмы , граф Дюрера , граф полезности К _3,3 , восьмивершинный граф, полученный из графа полезности преобразованием Y-Δ и 14-вершинным обобщенным графом Петерсена G (7,2) . Из этих графов первые четыре являются плоскими . Это единственные четыре кубических многогранных графа (графы простых выпуклых многогранников ), которые хорошо покрыты. Четыре графа (две призмы, граф Дюрера и G (7,2) ) являются обобщенными графами Петерсена.

Все 1- и 2-связные кубические хорошо покрытые графы образуются путем замены узлов пути или цикла тремя фрагментами графов, которые (1993) называет A , B и C. Пламмер Фрагменты A или B могут использоваться для замены узлов цикла или внутренних узлов пути, а фрагмент C используется для замены двух конечных узлов пути. Фрагмент A содержит мост , поэтому результатом выполнения этого процесса замены на пути и использования фрагмента A для замены некоторых узлов пути (и двух других фрагментов для оставшихся узлов) является 1-связная кубическая хорошо покрытая график. Все 1-связные кубические хорошо покрытые графы имеют этот вид, и все такие графы плоские.

Существует два типа 2-вершинно-связных кубических хорошо покрытых графов. Одно из этих двух семейств образуется путем замены узлов цикла фрагментами A и B , причем по крайней мере два из фрагментов относятся к типу A ; граф этого типа планарен тогда и только тогда, когда он не содержит фрагментов B. типа Другое семейство образуется путем замены узлов пути фрагментами типа B и C ; все такие графы плоские.

В дополнение к характеристике хорошо покрытых простых многогранников в трех измерениях исследователи также рассмотрели хорошо покрытые симплициальные многогранники или, что то же самое, хорошо покрытые максимальные планарные графы. Каждый максимальный планарный граф с пятью или более вершинами имеет связность вершин 3, 4 или 5. Не существует хорошо покрытых 5-связных максимальных плоских графов, а есть только четыре 4-связных хорошо покрытых максимальных плоских графа: графы правильного октаэдра , пятиугольной дипирамиды , курносого дисфеноида и неправильного многогранника (невыпуклого дельтаэдр ) с 12 вершинами, 30 ребрами и 20 треугольными гранями. Однако существует бесконечно много 3-связных хорошо покрытых максимальных плоских графов. Например, если максимальный планарный граф с 3 t вершинами имеет t непересекающихся треугольных граней, то эти грани образуют кликовое покрытие. Следовательно, конструкция кликового покрытия, которая для этих графов состоит из разделения каждого из этих t треугольников на три новых треугольника, пересекающихся в центральной вершине, дает хорошо покрытый максимальный планарный граф.

Сложность

Проверка того, содержит ли граф два максимальных независимых набора разных размеров, является NP-полной ; то есть, кроме того, проверка того, хорошо ли покрыт граф, является coNP-полной. Хотя в графах, которые, как известно, хорошо покрыты, легко найти максимальное независимое множество, для алгоритма также NP-трудно создать на выходе на всех графах либо максимальное независимое множество, либо гарантию того, что входные данные являются не очень хорошо покрыто.

Напротив, можно проверить, данный граф G очень ли хорошо покрыт за полиномиальное время . Для этого найдите подграф H графа G, состоящий из ребер, которые удовлетворяют двум свойствам совмещенного ребра в очень хорошо покрытом графе, а затем используйте алгоритм сопоставления, чтобы проверить, имеет ли H идеальное сопоставление. Некоторые задачи, которые являются NP-полными для произвольных графов, такие как проблема нахождения гамильтонова цикла , также могут быть решены за полиномиальное время для очень хорошо покрытых графов.

Граф называется эквисовместимым , если каждое максимальное паросочетание является максимальным; то есть он эквисовместим, если его линейный график хорошо покрыт. В более строгом смысле оно называется случайно сопоставляемым , если каждое максимальное паросочетание является совершенным паросочетанием . Единственными связными графами, сопоставляемыми случайным образом, являются полные графы и сбалансированные полные двудольные графы. Можно проверить, граф без когтей за полиномиальное время. хорошо ли покрыт линейный график или, в более общем смысле,

Характеристики хорошо покрытых графов с обхватом пять или более, а также хорошо покрытых графов, которые являются 3-регулярными, также приводят к эффективным алгоритмам с полиномиальным временем для распознавания этих графов.

Ссылки

• Берге, Клод (1981), «Некоторые общие свойства регуляризуемых графов, графов с критическим краем и B -графов», Теория графов и алгоритмы (Proc. Sympos., Res. Inst. Electr. Comm., Tohoku Univ., Сендай, 1980) , Конспект лекций по информатике, вып. 108, Берлин: Springer, стр. 108–123, номер документа : 10.1007/3-540-10704-5_10 , ISBN.  978-3-540-10704-0 0622929 МР   .
• Кэмпбелл, SR (1987), Некоторые результаты о плоских хорошо покрытых графах , доктор философии. диссертация, Университет Вандербильта, факультет математики . Цитируется Пламмером (1993) .
• Кэмпбелл, СР; Эллингем, Миннесота ; Ройл, Гордон Ф. (1993), «Характеристика хорошо покрытых кубических графов», Журнал комбинаторной математики и комбинаторных вычислений , 13 : 193–212, MR   1220613 .
• Кэмпбелл, Стивен Р.; Пламмер, Майкл Д. (1988), «О хорошо покрытых трехмерных многогранниках», Ars Combinatoria , 25 (A): 215–242, MR   0942505 .
• Каро, Яир; Себё, Андраш ; Тарси, Майкл (1996), «Распознавание жадных структур», Журнал алгоритмов , 20 (1): 137–156, doi : 10.1006/jagm.1996.0006 , MR   1368720 .
• Хватал, Вацлав ; Слейтер, Питер Дж. (1993), «Заметки о хорошо покрытых графах», Quo vadis, теория графов? , Анналы дискретной математики, вып. 55, Амстердам: Северная Голландия, стр. 179–181, MR   1217991 .
• Кук, Дэвид II; Нагель, Уве (2010), «Графы Коэна-Маколея и грани-векторы комплексов флагов», SIAM Journal on Discrete Mathematics , 26 : 89–101, arXiv : 1003.4447 , Bibcode : 2010arXiv1003.4447C , doi : 10.1137/100818170 .
• Дохтерманн, Антон; Энгстрем, Александр (2009), «Алгебраические свойства краевых идеалов через комбинаторную топологию», Электронный журнал комбинаторики , 16 (2): Исследовательская статья 2, doi : 10.37236/68 , MR   2515765 .
• Фаварон, О. (1982), «Очень хорошо покрытые графики», Discrete Mathematics , 42 (2–3): 177–187, doi : 10.1016/0012-365X(82)90215-1 , MR   0677051 .
• Финбоу, AS; Хартнелл, Б.Л. (1983), «Игра, связанная с покрытием звездами», Ars Combinatoria , 16 (A): 189–198, MR   0737090 .
• Финбоу, А.; Хартнелл, Б.; Новаковски, Р. (1988), «Графы с сильным доминированием: коллекция хорошо покрытых графов», Ars Combinatoria , 25 (A): 5–10, MR   0942485 .
• Финбоу, А.; Хартнелл, Б.; Новаковски, Р.Дж. (1993), «Характеристика хорошо покрытых графов обхвата 5 или больше», Журнал комбинаторной теории , серия B, 57 (1): 44–68, doi : 10.1006/jctb.1993.1005 , MR   1198396 .
• Финбоу, А.; Хартнелл, Б.; Новаковски, Р.; Пламмер, Майкл Д. (2003), «О хорошо покрытых триангуляциях. I», Discrete Applied Mathematics , 132 (1–3): 97–108, doi : 10.1016/S0166-218X(03)00393-7 , MR   2024267 .
• Финбоу, Артур С.; Хартнелл, Берт Л.; Новаковски, Ричард Дж.; Пламмер, Майкл Д. (2009), «О хорошо покрытых триангуляциях. II», Discrete Applied Mathematics , 157 (13): 2799–2817, doi : 10.1016/j.dam.2009.03.014 , MR   2537505 .
• Финбоу, Артур С.; Хартнелл, Берт Л.; Новаковски, Ричард Дж.; Пламмер, Майкл Д. (2010), «О хорошо покрытых триангуляциях. III», Discrete Applied Mathematics , 158 (8): 894–912, doi : 10.1016/j.dam.2009.08.002 , MR   2602814 .
• Финбоу, Артур С.; Хартнелл, Берт Л.; Новаковски, Ричард Дж.; Пламмер, Майкл Д. (2016), «Хорошо покрытые триангуляции: Часть IV», Discrete Applied Mathematics , 215 : 71–94, doi : 10.1016/j.dam.2016.06.030 , MR   3548980 .
• Финк, Дж. Ф.; Джейкобсон, MS; Кинч, Л.Ф.; Робертс, Дж. (1985), «О графах, имеющих доминирование половины их порядка», Период. Математика. Венгрия. , 16 (4): 287–293, doi : 10.1007/BF01848079 , MR   0833264 , S2CID   121734811 .
• Гринберг, Питер (1993), «Кусочная SL ₂ Z геометрия », Transactions of the American Mathematical Society , 335 (2): 705–720, doi : 10.2307/2154401 , JSTOR   2154401 , MR   1140914 .
• Холройд, Фред; Талбот, Джон (2005), «Графики со свойством Эрдеша-Ко-Радо», Discrete Mathematics , 293 (1–3): 165–176, arXiv : math/0307073 , doi : 10.1016/j.disc.2004.08.028 , МР   2136060 .
• Леск, М.; Пламмер, доктор медицины; Пуллибланк, WR (1984), «Равносогласованные графы», в Боллобасе, Бела (ред.), Теория графов и комбинаторика: материалы Кембриджской комбинаторной конференции, в честь Пола Эрдеша , Лондон: Academic Press, стр. 239– 254, МР   0777180 .
• Пламмер, Майкл Д. (1970), «Некоторые концепции, охватывающие графы», Journal of Combinatorial Theory , 8 : 91–98, doi : 10.1016/S0021-9800(70)80011-4 , MR   0289347 .
• Пламмер, Майкл Д. (1993), «Хорошо покрытые графики: обзор» , Quaestiones Mathematicae , 16 (3): 253–287, doi : 10.1080/16073606.1993.9631737 , MR   1254158 , заархивировано из оригинала 27 мая, 2012 .
• Рагхаван, Виджай; Спинрад, Джереми (2003), «Надежные алгоритмы для ограниченных областей», Journal of Algorithms , 48 ​​(1): 160–172, doi : 10.1016/S0196-6774(03)00048-8 , MR   2006100 , S2CID   16327087 .
• Равиндра, Г. (1977), «Хорошо покрытые графы», Журнал комбинаторики, информации и системных наук , 2 (1): 20–21, MR   0469831 .
• Шанкаранараяна, Рамеш С. (1994), Хорошо покрытые графы: некоторые новые подклассы и результаты по сложности (докторская диссертация), Университет Альберты
• Шанкаранараяна, Рамеш С.; Стюарт, Лорна К. (1992), «Результаты по сложности для хорошо покрытых графов», Networks , 22 (3): 247–262, CiteSeerX   10.1.1.47.9278 , doi : 10.1002/net.3230220304 , MR   1161178 .
• Стейплс, Дж. (1975), О некоторых подклассах хорошо покрытых графов , доктор философии. диссертация, Университет Вандербильта, факультет математики . Цитируется Пламмером (1993) .
• Самнер, Дэвид П. (1979), «Графы со случайным соответствием», Journal of Graph Theory , 3 (2): 183–186, doi : 10.1002/jgt.3190030209 , MR   0530304 .
• Танкус, Дэвид; Тарси, Майкл (1996), «Хорошо покрытые графы без когтей», Журнал комбинаторной теории , серия B, 66 (2): 293–302, doi : 10.1006/jctb.1996.0022 , MR   1376052 .
• Танкус, Дэвид; Тарси, Майкл (1997), «Структура хорошо покрытых графов и сложность проблем их распознавания», Журнал комбинаторной теории , серия B, 69 (2): 230–233, doi : 10.1006/jctb.1996.1742 , MR   1438624 .