Последняя звездчатость икосаэдра

Последняя звездчатость икосаэдра
Две симметричные ортогональные проекции
Тип	Звездчатый икосаэдр , 8 из 59.
Эйлер чар.	В виде звездчатого многогранника: F = 20 , E = 90 , V = 60 ( χ = −10 Как простой многогранник: F = 180 , E = 270 , V = 92 ( χ = 2)
Группа симметрии	икосаэдрический ( I h )
Характеристики	Как звездчатый многогранник: вершинно-транзитивный , гране-транзитивный.

3D-модель конечной звездочки икосаэдра

В геометрии — полная или окончательная звездчатость икосаэдра. Это самая дальняя звездчатая диаграмма икосаэдра , икосаэдра она является «полной» и «окончательной», поскольку включает в себя все ячейки звездчатой ​​диаграммы . То есть каждые три пересекающиеся грани ядра икосаэдра пересекаются либо на вершине этого многогранника, либо внутри него. Его изучал Макс Брюкнер после открытия многогранника Кеплера-Пуансо . Его можно рассматривать как неправильный, простой и звездчатый многогранник .

Фон

Иоганн Кеплер в своей книге «Harmonices Mundi» применил процесс звездчатости , признав малый звездчатый додекаэдр и большой звездчатый додекаэдр правильными многогранниками. Однако Луи Пуансо в 1809 году заново открыл еще два: большой икосаэдр и большой додекаэдр . в 1812 году доказал Огюстен-Луи Коши , что существует только четыре правильных звездчатых многогранника, известных как многогранник Кеплера-Пуансо .

Модель Брюкнера

Брюкнер (1900) расширил теорию звездчатости за пределы правильных форм и определил десять звездчатостей икосаэдра, включая полную звездчатость . Уиллер (1924) опубликовал список из двадцати форм звездчатости (двадцать две, включая отражающие копии), включая полную звездчатость . Х. С. М. Коксетер , П. Дю Валь , Х. Т. Флатер и Дж. Ф. Петри в своей книге 1938 года «Пятьдесят девять икосаэдров» сформулировали набор правил звездчатости для правильного икосаэдра и дали систематическое перечисление пятидесяти девяти звездочек, которые соответствуют этим правилам. Полное созвездие упоминается в книге как восьмое. В Модели книге Веннингера « многогранников » последняя звездчатая форма икосаэдра включена как 17-я модель звездчатых икосаэдров с индексным номером W ₄₂ .

В 1995 году Эндрю Хьюм в своей Netlib многогранной базе данных назвал его ехиднаэдр , в честь ехидны , или колючего муравьеда, — небольшого млекопитающего , покрытого грубыми волосами и шипами и сворачивающегося в клубок, чтобы защитить себя.

Интерпретации

Как звездочка

Основная статья: Пятьдесят девять икосаэдров

Звездчатая диаграмма икосаэдра с пронумерованными ячейками. Полный икосаэдр состоит из всех ячеек звездчатой ​​формы, но видны только самые крайние области, отмеченные на диаграмме цифрой 13.

Звездчатость . многогранника расширяет грани многогранника в бесконечные плоскости и порождает новый многогранник, который ограничен этими плоскостями как гранями, а пересечения этих плоскостей - как ребрами В книге «Пятьдесят девять икосаэдров» перечислены звёздчатые формы правильного икосаэдра , в соответствии с набором правил, выдвинутых Дж. К. П. Миллером , включая полную звёздчатую форму . Символ Дюваля полной звездчатой ​​формы — H , поскольку он включает в себя все ячейки звездчатой ​​диаграммы до самого внешнего слоя «h» включительно.

Как простой многогранник

Многогранная модель может быть построена из 12 наборов граней, каждая из которых сложена в группу из пяти пирамид.

Будучи простым, видимым поверхностным многогранником, внешняя форма конечной звездчатой ​​формы состоит из 180 треугольных граней, которые являются крайними треугольными областями на звездчатой ​​диаграмме. Они соединяются по 270 ребрам, которые, в свою очередь, сходятся в 92 вершинах с эйлеровой характеристикой , равной 2.

92 вершины лежат на поверхностях трех концентрических сфер. Самая внутренняя группа из 20 вершин образует вершины правильного додекаэдра; следующий слой из 12 образуют вершины правильного икосаэдра; а внешний слой 60 образуют вершины неоднородного усеченного икосаэдра. Радиусы этих сфер находятся в соотношении

$${\sqrt {{\frac {3}{2}}\left(3+{\sqrt {5}}\right)}}\,:\,{\sqrt {{\frac {1}{2}}\left(25+11{\sqrt {5}}\right)}}\,:\,{\sqrt {{\frac {1}{2}}\left(97+43{\sqrt {5}}\right)}}\,.$$

Выпуклые оболочки каждой сферы вершин

Внутренний	Середина	Внешний	все трое
20 вершин	12 вершин	60 вершин	92 вершины
Додекаэдр	Икосаэдр	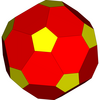Неоднородный усеченный икосаэдр	Полный икосаэдр

Если рассматривать его как трехмерный твердый объект с длиной ребра $a$, $\varphi a$, $\varphi ^{2}a$ и $\varphi ^{2}a{\sqrt {2}}$ (где $\varphi$ это золотое сечение ) полный икосаэдр имеет площадь поверхности

$$S={\frac {1}{20}}(13211+{\sqrt {174306161}})a^{2}\,,$$

и объем

$$V=(210+90{\sqrt {5}})a^{3}\,.$$

Как звездный многогранник

Двадцать граней многоугольника 9/4 (одна грань нарисована желтым цветом и отмечены 9 вершин).

2-изогональные грани 9/4

Полную звездчатую форму можно также рассматривать как самопересекающийся звездчатый многогранник, имеющий 20 граней, соответствующих 20 граням лежащего в основе икосаэдра. Каждое лицо представляет собой неправильный многоугольник со звездой 9/4 , или эннеаграмму . Поскольку три грани встречаются в каждой вершине, она имеет 20 × 9/3 = 60 вершин (это самый внешний слой видимых вершин и образуют кончики «шипов») и 20 × 9/2 = 90 ребер (каждое ребро вершины звездчатый многогранник включает в себя и соединяет два из 180 видимых ребер).

Если рассматривать звездчатый икосаэдр, то полная звездчатая форма представляет собой благородный многогранник , поскольку она одновременно изоэдральна (транзитивна по граням) и изогональна (транзитивна по вершинам).

Ссылки

• Брюкнер, Макс (1900). история ( Многоугольники и многогранники: теория и на немецком языке). Лейпциг: Б. Г. Треубнер. ISBN  978-1-4181-6590-1 .
• Коксетер, HSM (1973). Правильные многогранники (3-е изд.). Дувр. 3.6 6.2 Стулирование платоновых тел , стр. 96–104. ISBN  0-486-61480-8 .
• Коксетер, HSM; Дю Валь, П.; Флатер, ХТ; Петри, Дж. Ф. (1999) [1938]. Пятьдесят девять икосаэдров (3-е изд.). Тарквиний. ISBN  978-1-899618-32-3 . МР   0676126 .
• Кромвель, Питер Р. (1997). Многогранники . Издательство Кембриджского университета. ISBN  0-521-66405-5 .
• Дженкинс, Джеральд; Медведь, Магдалина (1985). Окончательная звездчатость икосаэдра: продвинутая математическая модель, которую можно вырезать и склеить . Tarquin Publications, Норфолк, Англия. ISBN  978-0-906212-48-6 .
• Пуансо, Луи (1810). «Память многоугольников и многогранников». Дж. из Политехнической школы . 9 :16–48.
• Уиллер, AH (1924). Некоторые формы икосаэдра и метод получения и обозначения высших многогранников . Учеб. Интерн. Математика. Конгресс, Торонто. Том. 1. С. 701–708.
• Веннингер, Магнус Дж . (1971). Модели многогранников . Издательство Кембриджского университета . ISBN  978-0-521-09859-5 .

Внешние ссылки

• С инструкцией по построению модели ехиднаэдра ( .doc ) Ральфа Джонса.
• К звездчатости икосаэдра и гранению додекаэдра Гай Инчбальд
• Вайсштейн, Эрик В. «Пятьдесят девять звездочек икосаэдра» . Математический мир .
  • Вайсштейн, Эрик В. «Ехиднаэдр» . Математический мир .
• Звездочки икосаэдра
• 59 звездочек икосаэдра
• VRML Модель : http://www.georgehart.com/virtual-polyhedra/vrml/echidnahedron.wrl
• Netlib : база данных многогранников, модель 141.

Известные звездочки икосаэдра
Обычный	Униформа двойная			Регулярные соединения			Обычная звезда	Другие
(Выпуклый) икосаэдр	Малый триамбический икосаэдр	Медиальный триамбический икосаэдр	Большой триамбический икосаэдр	Соединение пяти октаэдров	Соединение пяти тетраэдров	Соединение десяти тетраэдров	Большой икосаэдр	Раскопанный додекаэдр	Последняя звездочка
Звездчатый процесс на икосаэдре создает ряд родственных многогранников и соединений с икосаэдрической симметрией .