Усеченная треугольная мозаика порядка 7

Усеченная треугольная мозаика порядка 7
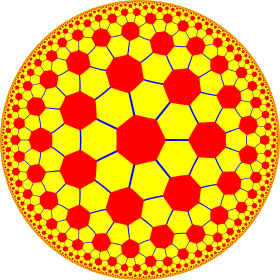Модель диска Пуанкаре гиперболической плоскости
Тип	Гиперболическая равномерная мозаика
Конфигурация вершин	7.6.6
Символ Шлефли	т{3,7}
Символ Витхоффа	2 7 \| 3
Диаграмма Кокстера
Группа симметрии	[7,3], (*732)
Двойной	Семиугольная черепица Гептакиса
Характеристики	Вершинно-транзитивный

В геометрии , усеченная треугольная мозаика порядка 7 иногда называемая гиперболическим футбольным мячом , ^[1] является полуправильным замощением гиперболической плоскости. расположены два шестиугольника и один семиугольник В каждой вершине , образующие узор, аналогичный обычному футбольному мячу ( усеченный икосаэдр ) с семиугольниками вместо пятиугольников . Он имеет символ Шлефли t{3,7}.

Гиперболический футбольный мяч (футбол)

Эту мозаику называют гиперболическим футбольным мячом (футболом) из-за ее сходства с узором усеченного икосаэдра, используемого на футбольных мячах. Небольшие его части в виде гиперболической поверхности можно построить в трехмерном пространстве.

Усеченный икосаэдр как многогранник и шар	Евклидова шестиугольная мозаика окрашенный как усеченный треугольная плитка	Бумажная конструкция гиперболического футбольного мяча

Двойная черепица

Двойная мозаика называется семиугольной мозаикой heptakis , названной в честь того, что ее можно построить как семиугольную мозаику , в которой каждый семиугольник разделен центральной точкой на семь треугольников.

Связанные мозаики

Эта гиперболическая мозаика топологически связана как часть последовательности однородных усеченных многогранников с конфигурациями вершин (n.6.6) и группы Кокстера симметрией [n,3].

* n 32 мутация симметрии усеченных мозаик: n .6.6 v т и
Sym. *n42 [n,3]	Spherical				Euclid.	Compact		Parac.	Noncompact hyperbolic
Sym. *n42 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Truncated figures
Config.	2.6.6	3.6.6	4.6.6	5.6.6	6.6.6	7.6.6	8.6.6	∞.6.6	12i.6.6	9i.6.6	6i.6.6
n-kis figures
Config.	V2.6.6	V3.6.6	V4.6.6	V5.6.6	V6.6.6	V7.6.6	V8.6.6	V∞.6.6	V12i.6.6	V9i.6.6	V6i.6.6

Из конструкции Витгофа есть восемь гиперболических однородных мозаик , которые могут быть основаны на регулярной семиугольной мозаике.

Если нарисовать плитки красного цвета на исходных гранях, желтого цвета в исходных вершинах и синего цвета по исходным краям, получится 8 форм.

Однородные семиугольные/треугольные мозаики v т и
Symmetry: $[7,3], (*732)$							$[7,3] +, (732)$


${7,3}$	$t{7,3}$	$r{7,3}$	$t{3,7}$	${3,7}$	$rr{7,3}$	$tr{7,3}$	$sr{7,3}$
Uniform duals


$V7 3$	$V3.14.14$	$V3.7.3.7$	$V6.6.7$	$V3 7$	$V3.4.7.4$	$V4.6.14$	$V3.3.3.3.7$

В популярной культуре

Это разбиение занимает видное место в HyperRogue .

См. также

Ссылки

^ КАК СОЗДАТЬ СОБСТВЕННУЮ МОДЕЛЬ ГИПЕРБОЛИЧЕСКОГО ФУТБОЛЬНОГО МЯЧА

Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
«Глава 10: Правильные соты в гиперболическом пространстве». Красота геометрии: двенадцать эссе . Дуврские публикации. 1999. ISBN 0-486-40919-8 . LCCN 99035678 .

Внешние ссылки

[1] КАК СОЗДАТЬ СОБСТВЕННУЮ МОДЕЛЬ ГИПЕРБОЛИЧЕСКОГО ФУТБОЛЬНОГО МЯЧА

[1]