Ромбические додекаэдрические соты
| Ромбические додекаэдрические соты | |
|---|---|
 | |
| Тип | выпуклый однородный сотовый двойной |
| Диаграмма Кокстера-Динкина | |
| Тип ячейки |  Ромбдодекаэдр V3.4.3.4 |
| Типы лица | Ромб |
| Космическая группа | Фм 3 м (225) |
| Обозначение Кокстера | ½ , [1 + ,4,3,4] , [4,3 1,1 ] ×2, <[3 [4] ]> |
| Двойной | тетраэдрически-октаэдрические соты |
| Характеристики | транзитивный по ребру , транзитивный по грани , транзитивный по ячейке |
Ромбические додекаэдрические соты (также додекаэдрилы ) , заполняющую пространство ) представляют собой мозаику (или соты , в евклидовом трехмерном пространстве. Это диаграмма Вороного гранецентрированной кубической упаковки сфер, которая имеет максимально плотную упаковку равных сфер в обычном пространстве (см. гипотезу Кеплера ).
Геометрия
[ редактировать ]Он состоит из копий единственной ячейки — ромбического додекаэдра . Все грани ромбы с диагоналями в соотношении 1: √ 2 . На каждом краю сходятся три ячейки. Таким образом, соты являются транзитивными по ячейкам , транзитивными по граням и транзитивными по краям ; но он не является вершинно-транзитивным , поскольку имеет два типа вершин. Вершины с тупыми ромбическими гранями имеют 4 ячейки. Вершины с острыми ромбическими гранями имеют 6 ячеек.
Ромбический додекаэдр можно скрутить в одном из своих шестиугольных сечений, чтобы сформировать трапециеромбический додекаэдр , который является ячейкой похожей мозаики — диаграммы Вороного гексагональной плотной упаковки .
 |  Соты можно получить из альтернативной мозаики куба, дополнив каждую грань каждого куба пирамидой. |  Вид изнутри ромбических додекаэдрических сот. |
Раскраски
[ редактировать ]Ячейки мозаики могут быть четырехцветными в квадратных слоях по два цвета в каждой, так что две ячейки одного цвета соприкасаются только в вершинах; или они могут быть шестицветными шестиугольными слоями по три цвета в каждом, так что клетки одного цвета вообще не имеют контакта.
| 4-раскраска | 6-раскраска |
|---|---|
 | 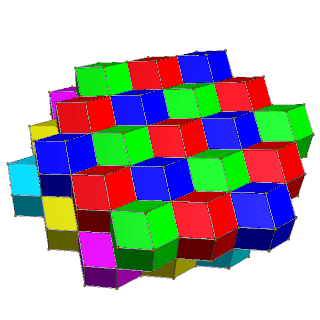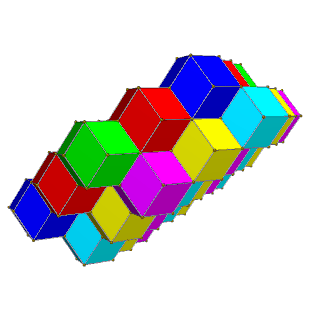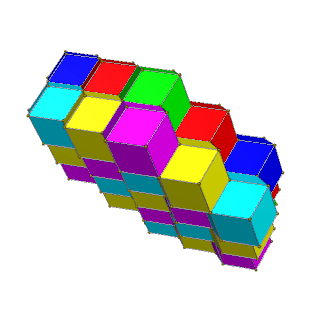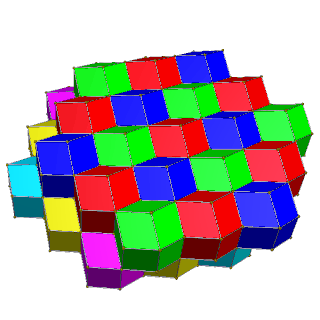 |
| Чередование квадратных слоев желтого/синего и красного/зеленого цветов. | Чередование шестиугольных слоев красного/зеленого/синего и пурпурного/желтого/голубого цветов. |
Связанные соты
[ редактировать ]Ромбико -додекаэдрические соты можно разделить на тригональные трапецоэдрические соты, при этом каждый ромбдодекаэдр расчленяется на 4 тригональных трапецоэдра . Каждый ромбдодекаэдр также можно разрезать с центральной точкой на 12 ромбических пирамид ромбических пирамидальных сот .
Трапезо-ромбические додекаэдрические соты
[ редактировать ]| Трапезо-ромбические додекаэдрические соты | |
|---|---|
 | |
| Тип | выпуклый однородный сотовый двойной |
| Тип ячейки | трапецоромбический додекаэдр ВГ3.4.3.4  |
| Типы лица | ромб , трапеция |
| Группа симметрии | P6 3 /ммц |
| Двойной | вращающиеся тетраэдрически-октаэдрические соты |
| Характеристики | однородный по краю, однородный по грани, однородный по ячейкам |
Трапецоромбические додекаэдрические соты представляют собой заполняющую пространство мозаику (или соты ) в евклидовом трехмерном пространстве. Он состоит из копий единственной ячейки — трапецоромбического додекаэдра . Он похож на более симметричные ромбические додекаэдрические соты, все 12 граней которых имеют форму ромбов.
Связанные соты
[ редактировать ]Это двойственный вершинно-транзитивным вращающимся тетраэдрально-октаэдрическим сотам .
Ромбические пирамидальные соты
[ редактировать ]| Ромбические пирамидальные соты | |
|---|---|
| (Нет изображения) | |
| Тип | Двойные однородные соты |
| Диаграммы Кокстера-Динкина | |
| Клетка | ромбическая пирамида |
| Лица | Ромб Треугольник |
| Группы Кокстера | [4,3 1,1 ], [3 [4] ], |
| Группа симметрии | Фм 3 м (225) |
| вершинные фигуры | |
| Двойной | Кантические кубические соты |
| Характеристики | Клеточно-транзитивный |
Ромбические пирамидальные соты или полусплюснутый октаэдр представляют собой однородную, заполняющую пространство мозаику (или соты ) в евклидовом трехмерном пространстве.
Эту соту можно рассматривать как ромбдодекаэдрическую соту с ромбическими додекаэдрами , рассеченными в центре на 12 ромбических пирамид.
 ромбические додекаэдрические соты | 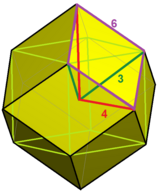 Ромбоэдрическое рассечение |  Внутри куба |
Связанные соты
[ редактировать ]Он двойствен кантическим кубическим сотам :
См. также
[ редактировать ]Ссылки
[ редактировать ]- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. с. 168. ИСБН 0-486-23729-Х .





