Изоэдральная фигура

В геометрии мозаика размерности 2 3 (плоская мозаика) или выше, или многогранник размерности если ( многогранник ) или выше, является изоэдральным или гране-транзитивным, все его грани одинаковы. Точнее, все грани должны быть не просто конгруэнтны , но и транзитивны , т. е. должны лежать на одной и той же орбите симметрии . Другими словами, для любых двух граней A и B должна существовать симметрия всей фигуры посредством перемещений , вращений и/или отражений которые отображают A на B. , По этой причине выпуклые равногранные многогранники представляют собой формы, из которых можно сделать игральные кости . [1]
Изоэдральные многогранники называются изоэдрами . Их можно описать по конфигурации лица . У изоэдра четное количество граней.
Двойственный , т.е. изоэдральному многограннику является вершинно-транзитивным изогональным. Каталонские тела , бипирамиды и трапецоэдры являются изоэдрическими. Они являются двойниками (изогональных) архимедовых тел , призм и антипризм соответственно. Платоновы тела , которые либо самодвойственны, либо двойственны другому Платонову телу, являются транзитивными по вершинам, ребрам и граням (т. е. изогональными, изотоксальными и изоэдральными).
Форма, которая является изоэдральной, имеет правильные вершины, а также является транзитивной по ребрам (т.е. изотоксальной), называется квазирегулярной двойственной формой. Некоторые теоретики считают эти фигуры действительно квазирегулярными, поскольку они обладают одной и той же симметрией, но это не является общепринятым.
Многогранник, который является равногранным и изогональным, называется благородным .
Не все изозоноэдры [2] являются изоэдрическими. [3] Например, ромбический икосаэдр является изозоноэдром, но не изоэдром. [4]
Примеры
[ редактировать ]| Выпуклый | Вогнутый | ||
|---|---|---|---|
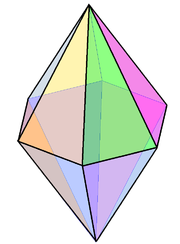 Шестиугольные бипирамиды , V4.4.6, представляют собой неправильные равногранные многогранники. |  Пятиугольная мозаика Каира , V3.3.4.3.4, изоэдральна. |  Ромбидодекаэдрические соты изоэдральны (и изохорны, и заполняют пространство). |  Квадратная мозаика, искаженная в спиральную мозаику H (топологически эквивалентную), по-прежнему остается изоэдральной. |
Классы изоэдров по симметрии
[ редактировать ]| Лица | Лицо конфиг. | Сорт | Имя | Симметрия | Заказ | Выпуклый | Копланарный | Невыпуклый |
|---|---|---|---|---|---|---|---|---|
| 4 | V3 3 | Платонический | тетраэдр тетрагональный дисфеноид ромбический дисфеноид | Т д , [3,3], (*332) Д 2д , [2 + ,2], (2*) Д 2 , [2,2] + , (222) | 24 4 4 4 |   | ||
| 6 | V3 4 | Платонический | куб трехугольный трапецоэдр асимметричный тригональный трапецоэдр | О ч , [4,3], (*432) Д 3д , [2 + ,6] (2*3) Д 3 [2,3] + , (223) | 48 12 12 6 |   | ||
| 8 | V4 3 | Платонический | октаэдр квадратная бипирамида ромбическая бипирамида квадратный скаленоэдр | О ч , [4,3], (*432) Д 4h ,[2,4],(*224) Д 2h ,[2,2],(*222) Д 2д , [2 + ,4],(2*2) | 48 16 8 8 |      |  | |
| 12 | V3 5 | Платонический | правильный додекаэдр пиритоэдр тетартоид | I h , [5,3], (*532) Т ч , [3 + ,4], (3*2) Т, [3,3] + , (*332) | 120 24 12 |   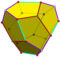 | 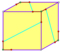 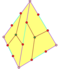 |   |
| 20 | V5 3 | Платонический | правильный икосаэдр | I h , [5,3], (*532) | 120 |  | ||
| 12 | Версия 3.6 2 | каталонский | триакис тетраэдр | Т д , [3,3], (*332) | 24 |  |   |  |
| 12 | V(3.4) 2 | каталонский | ромбический додекаэдр дельтовидный додекаэдр | О ч , [4,3], (*432) Т д , [3,3], (*332) | 48 24 |    |  |   |
| 24 | Версия 3.8 2 | каталонский | триакис октаэдр | О ч , [4,3], (*432) | 48 |  |   | |
| 24 | Версия 4.6 2 | каталонский | тетракис шестигранник | О ч , [4,3], (*432) | 48 |   |   |   |
| 24 | Версия 3.4 3 | каталонский | дельтовидный икоситетраэдр | О ч , [4,3], (*432) | 48 |  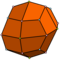 |    |  |
| 48 | Версия 4.6.8 | каталонский | Додекаэдр Дисдякиса | О ч , [4,3], (*432) | 48 |  |    |   |
| 24 | V3 4 .4 | каталонский | пятиугольный икоситетраэдр | О, [4,3] + , (432) | 24 |  | ||
| 30 | V(3.5) 2 | каталонский | ромбический триаконтаэдр | I h , [5,3], (*532) | 120 |  | ||
| 60 | Версия 3.10 2 | каталонский | триакис икосаэдр | I h , [5,3], (*532) | 120 |  |     | |
| 60 | Версия 5.6 2 | каталонский | пентакис додекаэдр | I h , [5,3], (*532) | 120 |  |      | |
| 60 | Версия 3.4.5.4 | каталонский | дельтовидный шестиконтаэдр | I h , [5,3], (*532) | 120 |  |  |  |
| 120 | Версия 4.6.10 | каталонский | триаконтаэдр дисдиакиса | I h , [5,3], (*532) | 120 |  |    |    |
| 60 | V3 4 .5 | каталонский | пятиугольный шестиконтаэдр | Я, [5,3] + , (532) | 60 |  | ||
| 2 н | V3 3 . н | Полярный | трапецоэдр асимметричный трапецоэдр | Д н д , [2 + ,2n ] , (2* n ) Д н , [2, н ] + , ( 22н ) | 4 n 2 н |  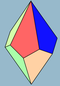    | ||
| 2 н 4 n | V4 2 . н V4 2 .2 н V4 2 .2 н | Полярный | правильная n - бипирамида изотоксал 2 н -бипирамида 2 n - скаленоэдр | D n h , [2, n ], (*22 n ) D n h , [2, n ], (*22 n ) Д н д , [2 + ,2n ] , (2* n ) | 4 n |    |     |
к -изоэдральная фигура
[ редактировать ]Многогранник (или многогранник в целом) является k -изоэдральным , если он содержит k граней в фундаментальных областях своей симметрии. [5] Аналогично, k -изоэдральная мозаика имеет k отдельных орбит симметрии (она может содержать m различных форм граней для m = k или только для некоторого m < k ). [6] («1-изоэдральный» — то же самое, что «изоэдральный».)
Моноэдральный . многогранник или моноэдральная мозаика ( m = 1) имеет конгруэнтные грани, прямо или отражательно, которые встречаются в одной или нескольких позициях симметрии М - гранный многогранник или мозаика имеет m различных форм граней (« двугранник », « трехгранник »… то же самое, что «2-гранник», «3-гранник»… соответственно). [7]
Вот несколько примеров k -изоэдральных многогранников и мозаик, грани которых окрашены в соответствии с их позициями симметрии k :
| 3-изоэдрический | 4-изоэдрический | изоэдрический | 2-изоэдрический |
|---|---|---|---|
| 2-гранные правильные многогранники | Моноэдральные многогранники | ||
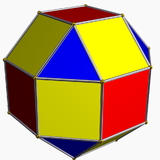 | 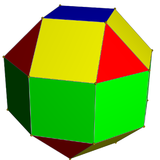 | 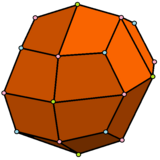 | 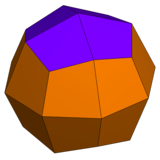 |
| Ромбокубооктаэдр имеет 1 тип треугольника и 2 типа квадрата. | Псевдоромбокубооктаэдр имеет 1 тип треугольника и 3 типа квадрата. | Дельтоидный икоситетраэдр имеет 1 тип грани. | Псевдодельтоидный икоситетраэдр имеет два типа граней одинаковой формы. |
| 2-изоэдрический | 4-изоэдрический | изоэдрический | 3-изоэдрический |
|---|---|---|---|
| 2-эдральные правильные грани | Моноэдральные мозаики | ||
 |  |  |  |
| Плитка Пифагора имеет 2 типа (размера) квадратов. | Эта 3-однородная плитка имеет 3 типа треугольников одинаковой формы и 1 тип квадрата. | Узор «елочка» имеет 1 тип прямоугольника. | Эта пятиугольная плитка имеет 3 типа неправильных пятиугольников одинаковой формы. |
Связанные термины
[ редактировать ]Ячеисто -транзитивная или изохорная фигура представляет собой n - многогранник ( n ≥ 4) или n - соты ( n которых ≥ 3), ячейки конгруэнтны и транзитивны друг другу. В трех измерениях катоптрические соты , двойственные однородным сотам, изохорны. В 4-х измерениях изохорные многогранники пронумерованы до 20 ячеек. [8]
Фасетно -транзитивная или изотопическая фигура представляет собой n -мерный многогранник или соту с ее гранями (( n −1) -гранями ), конгруэнтными и транзитивными. Двойственным изотопу является изогональный многогранник . По определению это изотопическое свойство является общим для двойственных однородных многогранников .
- Изотопическая двумерная фигура является изотоксальной, т. е. транзитивной по ребру.
- Изотопическая трехмерная фигура является изоэдральной, т. е. грани-транзитивной.
- Изотопная 4-мерная фигура изохорна, т.е. клеточно-транзитивна.
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Маклин, К. Робин (1990), «Подземелья, драконы и кости», The Mathematical Gazette , 74 (469): 243–256, doi : 10.2307/3619822 , JSTOR 3619822 , S2CID 195047512 .
- ^ Вайсштейн, Эрик В. «Изозоноэдр» . mathworld.wolfram.com . Проверено 26 декабря 2019 г.
- ^ Вайсштейн, Эрик В. «Изоэдр» . mathworld.wolfram.com . Проверено 21 декабря 2019 г.
- ^ Вайсштейн, Эрик В. «Ромбический икосаэдр» . mathworld.wolfram.com . Проверено 21 декабря 2019 г.
- ^ Соколар, Джошуа Э.С. (2007). «Шестиугольные паркетные плитки: k -изоэдральные монолиты со сколь угодно большим k » (исправленный PDF) . Математический интеллект . 29 : 33–38. arXiv : 0708.2663 . дои : 10.1007/bf02986203 . S2CID 119365079 . Проверено 9 сентября 2007 г.
- ^ Крейг С. Каплан, «Вводная теория мозаики для компьютерной графики». Архивировано 8 декабря 2022 г. в Wayback Machine , 2009 г., Глава 5: «Изоэдральные мозаики», стр. 35.
- ^ Плитки и узоры , с. 20, 23.
- ^ «Четырехмерные игральные кости до двадцати сторон» .
Внешние ссылки
[ редактировать ]- Ольшевский, Георгий. «Изотоп» . Глоссарий по гиперпространству . Архивировано из оригинала 4 февраля 2007 года.
- Вайсштейн, Эрик В. «Изоэдральная черепица» . Математический мир .
- Вайсштейн, Эрик В. «Изоэдр» . Математический мир .
- изоэдры 25 классов изоэдров с конечным числом сторон
- Дизайн игральных костей в The Dice Lab

