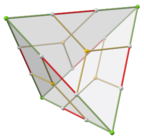
Додекаэдр

Эта статья о трехмерной форме. Не путать с римским додекаэдром .

Обыкновенные додекаэдры

Я ч , заказываю 120
Обычный-	Маленький звездчатый-	Большой-	Отличный звездчатый-
Т ч , заказ 24	Т, заказ 12	Ох 48 , закажи	Джонсон (J 84 )
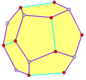
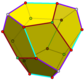
Пиритоэдр	Тетартоид	Ромбический-	Треугольный-
Д 4ч , заказ 16		Д 3ч , заказ 12
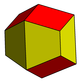
Ромбо-шестиугольный-	Ромбо-квадрат-	Трапезо-ромбический-	Ромбо-треугольный-

В геометрии — додекаэдр (от древнегреческого δωδεκαεδρον ( dōdekaedron ) ; от δοδεκα ( dṓdeka ) «двенадцать», и ἕδρα ( hédra ) «основание, посадочное место, грань») или дуодекаэдр. – это любой многогранник с двенадцатью плоскими гранями. Самый известный додекаэдр — это правильный додекаэдр с правильными пятиугольниками в качестве граней, который является платоновым телом . Также существуют три правильных звездчатых додекаэдра , которые построены в виде звездочек выпуклой формы. Все они имеют икосаэдрическую симметрию порядка 120.

Некоторые додекаэдры имеют ту же комбинаторную структуру, что и правильный додекаэдр (с точки зрения графа, образованного его вершинами и ребрами), но их пятиугольные грани не являются правильными:Пиритоэдр пиритоэдрическую , распространенная кристаллическая форма пирита , имеет симметрию , а тетартоид — тетраэдрическую симметрию .

Ромбический додекаэдр можно рассматривать как предельный случай пиритоэдра и он обладает октаэдрической симметрией . Варианты удлиненного додекаэдра и трапецоромбического додекаэдра , а также ромбических додекаэдров заполняют пространство . Есть множество других додекаэдров .

Хотя правильный додекаэдр имеет много общих черт с другими платоновыми телами, одно его уникальное свойство заключается в том, что можно начать с угла поверхности и провести через фигуру бесконечное количество прямых линий, которые возвращаются в исходную точку, не пересекая любую другую. угол.

Правильный додекаэдр

Основная статья: Правильный додекаэдр

Выпуклый правильный додекаэдр является одним из пяти правильных платоновых тел и может быть представлен символом Шлефли {5, 3}.

Двойственный многогранник — это правильный икосаэдр {3, 5}, имеющий пять равносторонних треугольников вокруг каждой вершины.

Четыре вида правильных додекаэдров

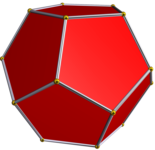Выпуклый правильный додекаэдр

Малый звездчатый додекаэдр

Большой додекаэдр

Большой звездчатый додекаэдр

Выпуклый правильный додекаэдр также имеет три звездчатых элемента , все из которых являются правильными звездчатыми додекаэдрами. Они образуют три из четырех многогранников Кеплера–Пуансо . Это малый звездчатый додекаэдр {5/2, 5}, большой звездчатый додекаэдр {5, 5/2} и большой звездчатый додекаэдр {5/2, 3}. Малый звездчатый додекаэдр и большой додекаэдр двойственны друг другу; большой звездчатый додекаэдр двойственен большому икосаэдру {3, 5/2}. Все эти правильные звездчатые додекаэдры имеют правильные пятиугольные или пентаграммные грани. Выпуклый правильный додекаэдр и большой звездчатый додекаэдр — это разные реализации одного и того же абстрактного правильного многогранника ; малый звездчатый додекаэдр и большой додекаэдр — это разные реализации другого абстрактного правильного многогранника.

Другие пятиугольные додекаэдры

В кристаллографии два важных додекаэдра могут встречаться как кристаллические формы в некоторых классах симметрии кубической кристаллической системы , которые топологически эквивалентны правильному додекаэдру, но менее симметричны: пиритоэдр с пиритоэдрической симметрией и тетартоид с тетраэдрической симметрией :

Пиритоэдр

Пиритоэдр
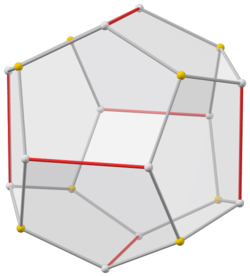(См. здесь вращающуюся модель.)
Лицевой многоугольник	равнобедренный пятиугольник
Диаграммы Кокстера
Лица	12
Края	30 (6 + 24)
Вершины	20 (8 + 12)
Группа симметрии	Т ч , [4,3 + ], (3*2), порядок 24
Группа вращения	Т , [3,3] + , (332), порядок 12
Двойной многогранник	Псевдойкосаэдр
Характеристики	лицо переходное
Сеть

Пиритоэдр — это додекаэдр с пиритоэдрической (T _h ) симметрией. Как и правильный додекаэдр , он имеет двенадцать одинаковых пятиугольных граней, по три сходящихся в каждой из 20 вершин (см. рисунок). Однако пятиугольники не обязательно должны быть правильными, а лежащее в их основе расположение атомов не имеет истинной оси симметрии пятого порядка. Его 30 ребер разделены на два набора — содержащие 24 и 6 ребер одинаковой длины. Единственными осями вращательной симметрии являются три взаимно перпендикулярные оси двойного порядка и четыре оси тройного порядка.

Хотя в кристаллах не существует правильных додекаэдров, форма пиритоэдра встречается в кристаллах минерала пирита и может послужить вдохновением для открытия правильной платоновской твердой формы. Истинный правильный додекаэдр может иметь форму квазикристаллов (таких как квазикристалл гольмия-магния-цинка ) с икосаэдрической симметрией , которая включает в себя истинные оси вращения пятого порядка.

Двойные позиции в моделях кристаллов пирита

Кристаллический пирит

Название «кристаллический пирит» из двух распространенных кристаллических форм пирита происходит от одного (второй — куб ). В пиритоэдрическом пирите грани имеют индекс Миллера (210), что означает, что двугранный угол составляет 2 · арктан (2) ≈ 126,87 °, а каждая пятиугольная грань имеет один угол примерно 121,6 ° между двумя углами примерно 106,6 °. и противоположные два угла примерно 102,6°. Следующие формулы показывают размеры грани идеального кристалла (который редко встречается в природе).

${\text{Height}}={\frac {\sqrt {5}}{2}}\cdot {\text{Long side}}$

${\text{Width}}={\frac {4}{3}}\cdot {\text{Long side}}$

${\text{Short sides}}={\sqrt {\frac {7}{12}}}\cdot {\text{Long side}}$

Природный пирит (с углами граней справа)

Декартовы координаты

Восемь вершин куба имеют координаты (±1, ±1, ±1).

Координаты 12 дополнительных вершин: ( 0, ±(1 + час ), ±(1 - час ² ) ) , ( ±(1 + час ), ±(1 - час ² ), 0 ) и ( ±(1 − ч ² ), 0, ±(1 + h ) ) .

h — высота клиновидной « крыши» над гранями куба с длиной ребра 2.

Важный случай: h = ⁠ 1/2 Вейра ⁠ структуре (четверть длины ребра куба) для идеального природного пирита (также пиритоэдра в – Фелана ).

Еще один: h = ⁠ 1 / φ ⁠ = 0,618... для правильного додекаэдра . см. в разделе «Геометрическая свобода» Другие случаи .

Два пиритоэдра с перепутанными ненулевыми координатами находятся в двойственном положении друг к другу, как додекаэдры в соединении двух додекаэдров .

Ортографические проекции пиритоэдра с h = 1/2.

Высоты 1/2 и 1/ φ

showАнимации
Honeycomb of alternating convex and concave pyritohedra with heights between ±⁠1/φ⁠	Heights between 0 (cube) and 1 (rhombic dodecahedron)

Геометрическая свобода

Пиритоэдр имеет геометрическую степень свободы с предельными случаями кубической выпуклой оболочки на одном пределе коллинеарных ребер и ромбического додекаэдра на другом пределе, поскольку 6 ребер вырождены до нулевой длины. Правильный додекаэдр представляет собой особый промежуточный случай, когда все ребра и углы равны.

Эти предельные случаи можно обойти, создав вогнутые или невыпуклые пиритоэдры. Эндододекаэдр ; вогнутый и равносторонний он может мозаику пространства с помощью выпуклого правильного додекаэдра. Продолжая отсюда в том же направлении, мы проходим через вырожденный случай, когда двенадцать вершин совпадают в центре, и переходим к правильному большому звездчатому додекаэдру, где все ребра и углы снова равны, а грани искажены в правильные пентаграммы . С другой стороны, за ромбическим додекаэдром, мы получаем невыпуклый равносторонний додекаэдр с самопересекающимися равносторонними пятиугольными гранями в форме рыбы.

showОсобые случаи пиритоэдра
Versions with equal absolute values and opposing signs form a honeycomb together. (Compare this animation.) The ratio shown is that of edge lengths, namely those in a set of 24 (touching cube vertices) to those in a set of 6 (corresponding to cube faces).
Ratio	1 : 1	0 : 1	1 : 1	2 : 1	1 : 1	0 : 1	1 : 1
h	−⁠√5 + 1/2⁠	−1	⁠−√5 + 1/2⁠	0	⁠√5 − 1/2⁠	1	⁠√5 + 1/2⁠
	−1.618...		−0.618...		0.618...		1.618...
Image	Regular star, great stellated dodecahedron, with regular pentagram faces	Degenerate, 12 vertices in the center	The concave equilateral dodecahedron, called an endo-dodecahedron.	A cube can be divided into a pyritohedron by bisecting all the edges, and faces in alternate directions.	A regular dodecahedron is an intermediate case with equal edge lengths.	A rhombic dodecahedron is a degenerate case with the 6 crossedges reduced to length zero.	Self-intersecting equilateral dodecahedron

Тетартоид

Тетартоид Тетрагональный пятиугольный додекаэдр
(См. здесь вращающуюся модель.)
Лицевой многоугольник	неправильный пятиугольник
Обозначение Конвея	гТ
Лица	12
Края	30 (6+12+12)
Вершины	20 (4+4+12)
Группа симметрии	Т , [3,3] + , (332), порядок 12
Характеристики	выпуклая , грань транзитивная

Тетартоид тетраэдрический пятиугольный (также тетрагональный пятиугольный додекаэдр , пентагон-тритетраэдр и додекаэдр ) представляет собой додекаэдр с киральной тетраэдрической симметрией (T). Как и правильный додекаэдр , он имеет двенадцать одинаковых пятиугольных граней, по три сходящихся в каждой из 20 вершин. Однако пятиугольники не являются правильными, и фигура не имеет осей симметрии пятого порядка.

Хотя в кристаллах не существует правильных додекаэдров, существует тетартоидная форма. Название тетартоид происходит от греческого корня, обозначающего одну четверть, потому что он имеет одну четверть полной октаэдрической симметрии и половину пиритоэдрической симметрии. Минерал кобальтит может иметь такую ​​форму симметрии.

и симметрию твердого тела, Абстракции, разделяющие топологию могут быть созданы на основе куба и тетраэдра. В кубе каждая грань разделена пополам наклонным краем. В тетраэдре каждое ребро разделено на три части, и каждая новая вершина соединена с центром грани. (В обозначениях многогранников Конвея это гиротетраэдр.)

Ортографические проекции по 2- и 3-кратным осям.

Кубическая и тетраэдрическая форма

Кобальтит

showСвязь с додекаэдром дьяки

A tetartoid can be created by enlarging 12 of the 24 faces of a dyakis dodecahedron.(The tetartoid shown here is based on one that is itself created by enlarging 24 of the 48 faces of the disdyakis dodecahedron.) Chiral tetartoids based on the dyakis dodecahedron in the middle Crystal model The crystal model on the right shows a tetartoid created by enlarging the blue faces of the dyakis dodecahedral core. Therefore, the edges between the blue faces are covered by the red skeleton edges.

Декартовы координаты

Следующие точки являются вершинами тетартоидного пятиугольника при тетраэдрической симметрии :

( а , б , в ); (- а , - б , с ); (− ⁠ n / d ₁ ⁠ , − ⁠ n / d ₁ ⁠ , ⁠ н / д ₁ ⁠ ); (- с , - а , б ); (− ⁠ n / d ₂ ⁠ , ⁠ n / d ₂ ⁠ , ⁠ n / d ₂ ⁠ ),

при следующих условиях:

0 ≤ а ≤ б ≤ с ,

п = а ² с - до н.э. ² ,

д ₁ = а ² − аб + б ² + и − 2 до н.э. ,

д ₂ = а ² + аб + б ² − и − 2 до н. э .,

нд ₁ d ₂ ≠ 0 .

Геометрическая свобода

Правильный додекаэдр представляет собой тетартоид с симметрией, превышающей требуемую. Триакис -тетраэдр представляет собой вырожденный случай с 12 ребрами нулевой длины. (С точки зрения цветов, использованных выше, это означает, что белые вершины и зеленые края поглощаются зелеными вершинами.)

showВариации тетартоида от правильного додекаэдра до триакис-тетраэдра.

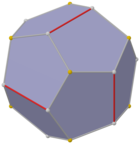
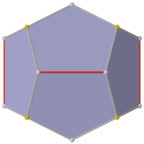
Двойной треугольный гиробиантикупол

Форма более низкой симметрии правильного додекаэдра может быть построена как двойственный многогранник, построенный из двух треугольных антикуполов, соединенных между собой основаниями, называемый треугольным гиробиантикуполом. Он имеет симметрию D _3d , порядок 12. Он состоит из 2 наборов по 3 одинаковых пятиугольника сверху и снизу, соединенных по 6 пятиугольников по бокам, которые чередуются вверх и вниз. Эта форма имеет шестиугольное поперечное сечение, и одинаковые копии можно соединить как частичную шестиугольную соту, но не все вершины будут совпадать.

Ромбический додекаэдр

Ромбический додекаэдр

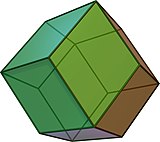
Ромбдодекаэдр представляет собой зоноэдр с двенадцатью ромбическими гранями и октаэдрической симметрией. Он двойственен квазиправильному кубооктаэдру ( архимедову телу ) и встречается в природе в виде кристалла. Ромбический додекаэдр складывается вместе, заполняя пространство.

Ромбический додекаэдр можно рассматривать как вырожденный пиритоэдр , в котором шесть особых ребер уменьшены до нулевой длины, превращая пятиугольники в ромбические грани.

Ромбдодекаэдр имеет несколько звездочек , первая из которых также является параллелоэдрическим заполнителем пространства .

Другой важный ромбический додекаэдр, додекаэдр Билинского , имеет двенадцать граней, конгруэнтных граням ромбического триаконтаэдра , то есть диагонали находятся в соотношении золотого сечения . Это также зоноэдр , описанный Билинским в 1960 году. Эта фигура является еще одним заполнителем пространства и может также встречаться в непериодических заполнениях пространства вместе с ромбическим триаконтаэдром, ромбическим икосаэдром и ромбическими шестигранниками.

Другие додекаэдры

Всего существует 6 384 634 топологически различных выпуклых додекаэдров, не считая зеркальных изображений — число вершин колеблется от 8 до 20. (Два многогранника «топологически различны», если они имеют существенно различное расположение граней и вершин, так что невозможно исказить один в другой, просто изменяя длины ребер или углы между ребрами или гранями.)

Топологически различные додекаэдры (исключая пятиугольные и ромбические формы)

• Однородные многогранники:
  • Десятиугольная призма – 10 квадратов, 2 декагона, D _{10h , порядок 40.} симметрия
  • Пятиугольная антипризма – 10 равносторонних треугольников, 2 пятиугольника, D _{5d , порядок 20.} симметрия
• Твердые тела Джонсона (обычная поверхность):
  • Пятиугольный купол – 5 треугольников, 5 квадратов, 1 пятиугольник, 1 десятиугольник, симметрия C _5v , порядок 10.
  • Курносый дисфеноид – 12 треугольников, D _2d , порядок 8.
  • Вытянутая квадратная дипирамида – 8 треугольников и 4 квадрата, D _{4h , порядок 16.} симметрия
  • Метабидиминидированный икосаэдр – 10 треугольников и 2 пятиугольника, C _{2v , порядок 4.} симметрия
• Конгруэнтное неправильное лицо: ( лицо-переходное )
  • Шестиугольная бипирамида – 12 равнобедренных треугольников , двойственная шестиугольной призме , D _{6h , порядок 24.} симметрия
  • Шестиугольный трапецоэдр – 12 змеев , двойная шестиугольная антипризма , D _{6d , порядок 24} симметрия
  • Триакис тетраэдр - 12 равнобедренных треугольников, двойственных усеченному тетраэдру , T _{d , порядок 24.} симметрия
• Другие менее регулярные лица:
  • Пятиугольная пирамида – 11 равнобедренных треугольников и 1 правильный пятиугольник , C _11v , порядок 11.
  • Трапецоромбический додекаэдр – 6 ромбов, 6 трапеций – двойственный треугольному ортобикуполу , D _{3h , порядок 12} симметрия
  • Ромбо-шестиугольный додекаэдр или вытянутый додекаэдр – 8 ромбов и 4 равносторонних шестиугольника , D _{4h , порядок 16.} симметрия
  • Усеченный пятиугольный трапецоэдр , D _5d , порядка 20, топологически эквивалентный правильному додекаэдру.

Практическое использование

Арманд Шпитц использовал додекаэдр в качестве эквивалента «глобуса» для своего проектора планетария Digital Dome . основано на предложении Альберта Эйнштейна .

См. также

• 120-ячеечный – правильный полихорон (4D-многогранник), поверхность которого состоит из 120 додекаэдрических ячеек.
• Braarudosphaera bigelowii в форме додекаэдра - кокколитофор ( одноклеточная -фитопланктон водоросль ).
• Додекаэдр Пентакиса
• Римский додекаэдр
• Курносый додекаэдр
• Усеченный додекаэдр

Внешние ссылки

• Четвертое тело Платона и «Пиритоэдр» , Пол Стивенсон, 1993, The Mathematical Gazette, Vol. 77, № 479 (июль 1993 г.), стр. 220–226 [1]
• Звездчатость пиритоэдра VRML-модели и анимация пиритоэдра и его звездочек
• Клитцинг, Ричард. «3D выпуклые однородные многогранники o3o5x – лань» .
• Редактируемая для печати развертка додекаэдра с интерактивным 3D-просмотром
• Однородные многогранники
• Многогранники оригами – модели, сделанные с помощью модульного оригами.
• Многогранники виртуальной реальности Энциклопедия многогранников
• К.Дж.М. Маклин, Геометрический анализ пяти платоновых тел и других полуправильных многогранников
• Додекаэдр 3D-визуализация
• Stella: Polyhedron Navigator : программное обеспечение, использованное для создания некоторых изображений на этой странице.
• Как сделать додекаэдр из пенопластового куба.