Группы точек в четырех измерениях


В геометрии группа точек в четырех измерениях — это группа изометрий в четырех измерениях, оставляющая начало координат фиксированным, или, соответственно, группа изометрий трехмерной сферы .
История четырехмерных групп
[ редактировать ]- 1889 Эдуард Гурса , Об ортогональных заменах и правильных делениях пространства , Annales Scientifiques de l'École Normale Supérieure, Ser. 3, 6, (стр. 9–102, стр. 80–81 тетраэдры), тетраэдр Гурса
- 1951, AC Hurley, Группы конечного вращения и кристаллические классы в четырех измерениях , Труды Кембриджского философского общества, том. 47, выпуск 04, с. 650 [1]
- 1962 А. Л. Маккей Браве Решетки в четырехмерном пространстве [2]
- 1964 Патрик дю Валь , Гомографии, кватернионы и вращения , кватернионов. 4D точечные группы на основе
- 1975 Ян Мозжимас, Анджей Солецкий, Точечные группы R4 , Отчеты по математической физике, Том 7, Выпуск 3, с. 363-394 [3]
- 1978 Х. Браун, Р. Бюлов, Дж. Нойбюзер, Х. Вондратчек и Х. Зассенхаус, Кристаллографические группы четырехмерного пространства. [4]
- 1982 Н. П. Уорнер, Группы симметрии правильных мозаик S2 и S3. [5]
- 1985 EJW Whittaker, Атлас гиперстереограмм четырехмерных кристаллических классов.
- 1985 HSM Коксетер , Регулярные и полуправильные многогранники II , Обозначение Кокстера для 4D точечных групп
- 2003 Джон Конвей и Смит, О кватернионах и октонионах , Завершенные кватернионов . 4D точечные группы на основе
- 2018 Н. В. Джонсон «Геометрии и преобразования» , главы 11,12,13, Полные полихорические группы, с. 249, дуопризматические группы с. 269
Изометрии четырехмерной точечной симметрии
[ редактировать ]Существует четыре основные изометрии четырехмерной точечной симметрии : симметрия отражения , симметрия вращения , симметрия ротора и двойное вращение .
Обозначения групп
[ редактировать ]Эту статью может потребовать очистки Википедии , чтобы она соответствовала стандартам качества . Конкретная проблема заключается в следующем: эта статья сильно дезорганизована и не имеет четкого представления о структуре. ( январь 2021 г. ) |
Группы точек в этой статье даны в нотации Кокстера , которые основаны на группах Кокстера , с разметкой для расширенных групп и подгрупп. [6] Обозначение Кокстера имеет прямое соответствие диаграмме Кокстера, например [3,3,3], [4,3,3], [3 1,1,1 ], [3,4,3], [5,3,3] и [p,2,q]. Эти группы связали 3-сферу в идентичные гиперсферические тетраэдрические домены. Количество доменов соответствует порядку группы. Число зеркал для неприводимой группы равно nh/2 , где h группы Кокстера — число Кокстера , n — размерность (4). [7]
Для перекрестных ссылок здесь также приведены основанные на кватернионах. обозначения Патрика Дю Валя (1964), [8] и Джон Конвей (2003). [9] Обозначения Конвея позволяют вычислять порядок группы как произведение элементов с порядками групп киральных многогранников: (T = 12, O = 24, I = 60). В обозначениях Конвея префикс (±) подразумевает центральную инверсию , а суффикс (.2) подразумевает зеркальную симметрию. Точно так же в обозначениях Дю Валя есть верхний индекс звездочки (*), обозначающий зеркальную симметрию.
Группы инволюции
[ редактировать ]Существует пять инволюционных групп: нет симметрии [ ] + , отражательная симметрия [ ], 2-кратная вращательная симметрия [2] + , 2-кратное роторное отражение [2 + ,2 + ] и симметрия центральной точки [2 + ,2 + ,2 + ] как 2-кратное двойное вращение .
Группы Кокстера 4-го ранга
[ редактировать ]Полихорическая группа — одна из пяти групп симметрии 4-мерных правильных многогранников . Существуют также три многогранные призматические группы и бесконечное множество дуопризматических групп. Каждая группа определяется тетраэдра Гурса, фундаментальной областью ограниченной зеркальными плоскостями. Двугранные углы между зеркалами определяют порядок двугранной симметрии . Диаграмма Коксетера-Дынкина представляет собой граф, узлы которого представляют зеркальные плоскости, а ребра называются ветвями и помечены порядком двугранных углов между зеркалами.
Термин полихорон (множественное число полихора , прилагательное полихорик ) происходит от греческих корней поли («много») и хорос («комната» или «пространство») и защищался. [10] Нормана Джонсона и Джорджа Ольшевского в контексте однородной полихоры (4-многогранников) и связанных с ними 4-мерных групп симметрии. [11]
B 4 можно разложить на 2 ортогональные группы, 4 A 1 и D 4 :
|
F 4 можно разложить на 2 ортогональные группы D 4 :
|
B 3 × A 1 можно разложить на ортогональные группы 4 A 1 и D 3 :
|
4-го ранга Группы Кокстера позволяют набору из 4 зеркал охватывать 4-пространство и делят 3-сферу на тетраэдрические фундаментальные области. Группы Кокстера более низкого ранга могут ограничивать только фундаментальные области осоэдра или гомотопа на 3-сфере.
Как и трехмерные многогранные группы , имена данных четырехмерных полихорических групп состоят из греческих префиксов количества ячеек соответствующих правильных многогранников с треугольными гранями. [12] Расширенные симметрии существуют в однородной полихоре с симметричными кольцевыми узорами в рамках конструкции диаграммы Коксетера . Киральные симметрии существуют в чередующейся однородной полихоре.
Только неприводимые группы имеют числа Кокстера, но дуопризматические группы [p,2,p] можно удвоить до p,2,p, добавив 2-кратное вращение к фундаментальной области, и это дает эффективное число Кокстера 2 p , для например, группа [4,2,4] и ее полная симметрия B 4 , [4,3,3] с числом Кокстера 8.
| Вейль группа | Конвей Кватернион | Абстрактный структура | Коксетер диаграмма | Коксетер обозначение | Заказ | Коммутатор подгруппа | Коксетер число (час) | Зеркала (м) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Полные полихорические группы | ||||||||||||
| A 4 | + 1 / 60 [I×I].2 1 | С 5 | [3,3,3] | 120 | [3,3,3] + | 5 | 10 | |||||
| Д 4 | ±1/3[T×T].2 | 1/2. 2 С 4 | [3 1,1,1 ] | 192 | [3 1,1,1 ] + | 6 | 12 | |||||
| Б 4 | ±1/6[O×O].2 | 2 С 4 = С 2 ≀ С 4 | [4,3,3] | 384 | 8 | 4 | 12 | |||||
| FF4 | ±1/2[O×O].2 3 | 3. 2 С 4 | [3,4,3] | 1152 | [3 + ,4,3 + ] | 12 | 12 | 12 | ||||
| Ч 4 | ±[I×I].2 | 2.(A 5 ×A 5 ).2 | [5,3,3] | 14400 | [5,3,3] + | 30 | 60 | |||||
| Полные многогранные призматические группы | ||||||||||||
| А 3 А 1 | +1/24[O×O].2 3 | S 4 ×D 1 | [3,3,2] = [3,3]×[ ] | 48 | [3,3] + | - | 6 | 1 | ||||
| Б 3 А 1 | ±1/24[O×O].2 | S 4 ×D 1 | [4,3,2] = [4,3]×[ ] | 96 | - | 3 | 6 | 1 | ||||
| Ч 3 А 1 | ±1/60[I×I].2 | A 5 ×D 1 | [5,3,2] = [5,3]×[ ] | 240 | [5,3] + | - | 15 | 1 | ||||
| Полные дуопризматические группы | ||||||||||||
| 4А 1 = 2Д 2 | ±1/2[D 4 ×D 4 ] | Д 1 4 = Д2 2 | [2,2,2] = [ ] 4 = [2] 2 | 16 | [ ] + | 4 | 1 | 1 | 1 | 1 | ||
| Д 2 Б 2 | ±1/2[D 4 ×D 8 ] | D 2 ×D 4 | [2,2,4] = [2]×[4] | 32 | [2] + | - | 1 | 1 | 2 | 2 | ||
| D2AD2A2 | ±1/2[D 4 ×D 6 ] | D 2 ×D 3 | [2,2,3] = [2]×[3] | 24 | [3] + | - | 1 | 1 | 3 | |||
| Д 2 Г 2 | ±1/2[D 4 ×D 12 ] | D 2 ×D 6 | [2,2,6] = [2]×[6] | 48 | - | 1 | 1 | 3 | 3 | |||
| Д 2 Ч 2 | ±1/2[D 4 ×D 10 ] | D 2 ×D 5 | [2,2,5] = [2]×[5] | 40 | [5] + | - | 1 | 1 | 5 | |||
| 2B2Б2 | ±1/2[D 8 ×D 8 ] | Д 4 2 | [4,2,4] = [4] 2 | 64 | [2 + ,2,2 + ] | 8 | 2 | 2 | 2 | 2 | ||
| B2AБ2А2 | ±1/2[D 8 ×D 6 ] | D 4 ×D 3 | [4,2,3] = [4]×[3] | 48 | [2 + ,2,3 + ] | - | 2 | 2 | 3 | |||
| Б 2 Г 2 | ±1/2[D 8 ×D 12 ] | D 4 ×D 6 | [4,2,6] = [4]×[6] | 96 | - | 2 | 2 | 3 | 3 | |||
| Б 2 Ч 2 | ±1/2[D 8 ×D 10 ] | D 4 ×D 5 | [4,2,5] = [4]×[5] | 80 | [2 + ,2,5 + ] | - | 2 | 2 | 5 | |||
| 2A2А2 | ±1/2[D 6 ×D 6 ] | Д 3 2 | [3,2,3] = [3] 2 | 36 | [3 + ,2,3 + ] | 6 | 3 | 3 | ||||
| A2GA2G2 | ±1/2[D 6 ×D 12 ] | D 3 ×D 6 | [3,2,6] = [3]×[6] | 72 | - | 3 | 3 | 3 | ||||
| 2Г 2 | ±1/2[D 12 ×D 12 ] | Д 6 2 | [6,2,6] = [6] 2 | 144 | 12 | 3 | 3 | 3 | 3 | |||
| A2HA2H2 | ±1/2[D 6 ×D 10 ] | D 3 ×D 5 | [3,2,5] = [3]×[5] | 60 | [3 + ,2,5 + ] | - | 3 | 5 | ||||
| G2HG2H2 | ±1/2[D 12 ×D 10 ] | D 6 ×D 5 | [6,2,5] = [6]×[5] | 120 | - | 3 | 3 | 5 | ||||
| 2H2H2 | ±1/2[D 10 ×D 10 ] | Д 5 2 | [5,2,5] = [5] 2 | 100 | [5 + ,2,5 + ] | 10 | 5 | 5 | ||||
| В общем, p,q=2,3,4... | ||||||||||||
| 2И 2 (2п) | ±1/2[D 4p ×D 4p ] | Д 2п 2 | [2п,2,2п] = [2п] 2 | 16р. 2 | [п + ,2,п + ] | 2р | п | п | п | п | ||
| 2И 2 (п) | ±1/2[D 2p ×D 2p ] | Д п 2 | [п,2,п] = [п] 2 | 4р 2 | 2р | п | п | |||||
| Я 2 (п)Я 2 (д) | ±1/2[D 4p ×D 4q ] | D 2p ×D 2q | [2p,2,2q] = [2p]×[2q] | 16pq | [п + ,2,д + ] | - | п | п | д | д | ||
| Я 2 (п)Я 2 (д) | ±1/2[D 2p ×D 2q ] | D p ×D q | [p,2,q] = [p]×[q] | 4pq | - | п | д | |||||
Порядок симметрии равен числу ячеек правильного полихорона, умноженному на симметрию его ячеек. Всеусеченная двойная полихора имеет клетки, соответствующие фундаментальным областям группы симметрии.
| Симметрия | A 4 | Д 4 | Б 4 | FF4 | Ч 4 | |
|---|---|---|---|---|---|---|
| 4-многогранник | 5-клеточный | полудессеракт | тессеракт | 24-ячеечный | 120-ячеечный | |
| Клетки | 5 {3,3} | 16 {3,3} | 8 {4,3} | 24 {3,4} | 120 {5,3} | |
| Симметрия клеток | [3,3], порядок 24 | [4,3], порядок 48 | [5,3], порядок 120 | |||
| Диаграмма Кокстера | ||||||
| 4-многогранник сеть |  | 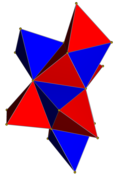 | 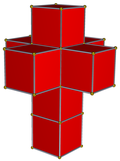 | 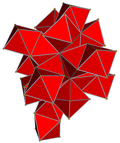 | 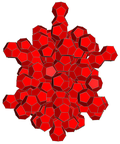 | |
| Всеобрезание | всеобщий. 5-клеточный | всем подводить | всеобщий. тессеракт | всеобщий. 24-ячеечный | всеобщий. 120-ячеечный | |
| Всеобрезание двойной сеть |  |  |  |  |  | |
| Диаграмма Кокстера | ||||||
| Клетки | 5×24 = 120 | (16/2)×24 = 192 | 8×48 = 384 | 24×48 = 1152 | 120×120 = 14400 | |
Хиральные подгруппы
[ редактировать ]


Прямые подгруппы отражающих 4-мерных точечных групп:
| Коксетер обозначение | Конвей Кватернион | Структура | Заказ | оси вращения | ||||
|---|---|---|---|---|---|---|---|---|
| Полихорические группы | ||||||||
| [3,3,3] + | +1/60[I× I ] | AА5 | 60 | 10 3 | 10 2 | |||
| 3,3,3 + | ±1/60[I× I ] | A 5 ×Z 2 | 120 | 10 3 | (10+?) 2 | |||
| [3 1,1,1 ] + | ±1/3[T×T] | 1/2. 2 A 4 | 96 | 16 3 | 18 2 | |||
| [4,3,3] + | ±1/6[O×O] | 2 A 4 = A 2 ≀A 4 | 192 | 6 4 | 16 3 | 36 2 | ||
| [3,4,3] + | ±1/2[O×O] | 3. 2 A 4 | 576 | 18 4 | 16 3 | 16 3 | 72 2 | |
| [3 + ,4,3 + ] | ±[T×T] | 288 | 16 3 | 16 3 | (72+18) 2 | |||
| [[3 + ,4,3 + ]] | ±[O×T] | 576 | 32 3 | (72+18+?) 2 | ||||
| 3,4,3 + | ±[O×O] | 1152 | 18 4 | 32 3 | (72+?) 2 | |||
| [5,3,3] + | ±[I×I] | 2.(A 5 ×A 5 ) | 7200 | 72 5 | 200 3 | 450 2 | ||
| Многогранные призматические группы | ||||||||
| [3,3,2] + | + 1 / 24 [O× O ] | A 4 ×Z 2 | 24 | 4 3 | 4 3 | (6+6) 2 | ||
| [4,3,2] + | ±1/24[O×O] | S 4 ×Z 2 | 48 | 6 4 | 8 3 | (3+6+12) 2 | ||
| [5,3,2] + | ±1/60[I×I] | A 5 ×Z 2 | 120 | 12 5 | 20 3 | (15+30) 2 | ||
| Дуопризматические группы | ||||||||
| [2,2,2] + | +1/2[D 4 ×D 4 ] | 8 | 1 2 | 1 2 | 4 2 | |||
| [3,2,3] + | +1/2[D 6 ×D 6 ] | 18 | 1 3 | 1 3 | 9 2 | |||
| [4,2,4] + | +1/2[D 8 ×D 8 ] | 32 | 1 4 | 1 4 | 16 2 | |||
| (p,q=2,3,4...), НОД(p,q)=1 | ||||||||
| [п,2,п] + | +1/2[D 2p ×D 2p ] | 2р 2 | 1 р | 1 р | (пп) 2 | |||
| [п,2,д] + | +1/2[D 2p ×D 2q ] | 2pq | 1 р | 1 кв. | (пк) 2 | |||
| [п + ,2,д + ] | +[C p ×C q ] | Z p ×Z q | ПК | 1 р | 1 кв. | |||
Пентахорическая симметрия
[ редактировать ]- Пентахорическая группа – A 4 , [3,3,3], (






 ), заказ 120, (Дю Валь #51' (I † /К 1 ;И/К 1 ) †* , Конвей + 1 / 60 [I×I].2 1 ), названный в честь 5-клеточного (пентахорона), заданного кольцевой диаграммой Кокстера.
), заказ 120, (Дю Валь #51' (I † /К 1 ;И/К 1 ) †* , Конвей + 1 / 60 [I×I].2 1 ), названный в честь 5-клеточного (пентахорона), заданного кольцевой диаграммой Кокстера. 





 . Ее также иногда называют гипертетраэдрической группой для расширения тетраэдрической группы [3,3]. В этой группе 10 зеркальных гиперплоскостей. Она изоморфна абстрактной симметрической группе S 5 .
. Ее также иногда называют гипертетраэдрической группой для расширения тетраэдрической группы [3,3]. В этой группе 10 зеркальных гиперплоскостей. Она изоморфна абстрактной симметрической группе S 5 . - Расширенная пентахорная группа Aut ( A 4 ) , [[3,3,3]], (на удвоение можно намекнуть с помощью свернутой диаграммы,


 ), заказ 240, (Дю Валь №51 (I †* /С 2 ;И/С 2 ) †* , Конвей ± 1 / 60 [I× I ].2). Она изоморфна прямому произведению абстрактных групп: S 5 ×C 2 .
), заказ 240, (Дю Валь №51 (I †* /С 2 ;И/С 2 ) †* , Конвей ± 1 / 60 [I× I ].2). Она изоморфна прямому произведению абстрактных групп: S 5 ×C 2 . - Хиральная расширенная пентахорная группа — это [[3,3,3]] + , (


 ), заказ 120, (Дю Валь №32 (I † /С 2 ;И/С 2 ) † , Конвей ± 1 / 60 [IX I ]). Данная группа представляет собой конструкцию omnisnub 5-cell ,
), заказ 120, (Дю Валь №32 (I † /С 2 ;И/С 2 ) † , Конвей ± 1 / 60 [IX I ]). Данная группа представляет собой конструкцию omnisnub 5-cell , 

 , хотя сделать его единым невозможно. Она изоморфна прямому произведению абстрактных групп: A 5 ×C 2 .
, хотя сделать его единым невозможно. Она изоморфна прямому произведению абстрактных групп: A 5 ×C 2 .
- Хиральная расширенная пентахорная группа — это [[3,3,3]] + , (
- Хиральная пентахорная группа - это [3,3,3] + , (






 ), порядок 60, (Дю Валь #32' (I † /К 1 ;И/К 1 ) † , Конвей + 1 / 60 [I× I ]). Она изоморфна абстрактной знакопеременной группе A 5 .
), порядок 60, (Дю Валь #32' (I † /К 1 ;И/К 1 ) † , Конвей + 1 / 60 [I× I ]). Она изоморфна абстрактной знакопеременной группе A 5 . - Расширенная киральная пентахорная группа : [[3,3,3] + ], заказ 120, (Дю Валь #51" (I † /К 1 ;И/К 1 ) – †* , Конвей + 1 / 60 [IxI].2 3 ). Коксетер относит эту группу к абстрактной группе (4,6|2,3). [13] Она также изоморфна симметрической группе S5 абстрактной .
- Расширенная пентахорная группа Aut ( A 4 ) , [[3,3,3]], (на удвоение можно намекнуть с помощью свернутой диаграммы,
Шестидекахорная симметрия
[ редактировать ]- Шестидесятеричная группа – B 4 , [4,3,3], (






 ), order 384, (Du Val #47 (O/V;O/V) * , Конвей ± 1 / 6 [O×O].2), названный в честь 16-клеточного (гексадекахорон),
), order 384, (Du Val #47 (O/V;O/V) * , Конвей ± 1 / 6 [O×O].2), названный в честь 16-клеточного (гексадекахорон), 





 . В этой группе 16 зеркальных гиперплоскостей, которые можно разделить на 2 ортогональных набора: 12 из [3 1,1,1 ] подгруппы и 4 из подгруппы [2,2,2]. Ее также называют гипероктаэдрической группой для расширения трехмерной октаэдрической группы [4,3] и тессерактической группой для тессеракта .
. В этой группе 16 зеркальных гиперплоскостей, которые можно разделить на 2 ортогональных набора: 12 из [3 1,1,1 ] подгруппы и 4 из подгруппы [2,2,2]. Ее также называют гипероктаэдрической группой для расширения трехмерной октаэдрической группы [4,3] и тессерактической группой для тессеракта . 





 .
. - Хиральная гексадекагорная группа - [4,3,3] + , (






 ), order 192, (Du Val #27 (O/V;O/V), Conway ± 1 / 6 [О×О]). Эта группа представляет собой конструкцию омниснубового тессеракта ,
), order 192, (Du Val #27 (O/V;O/V), Conway ± 1 / 6 [О×О]). Эта группа представляет собой конструкцию омниснубового тессеракта , 





 , хотя сделать его единым невозможно.
, хотя сделать его единым невозможно. - Ионная уменьшенная гексадекагорная группа — [4,(3,3) + ], (






 ), order 192, (Du Val #41 (T/V;T/V) * , Конвей ± 1 / 3 [Т×Т].2). Эта группа приводит к курносой 24-клеточной конструкции
), order 192, (Du Val #41 (T/V;T/V) * , Конвей ± 1 / 3 [Т×Т].2). Эта группа приводит к курносой 24-клеточной конструкции 





 .
. - Полугексадекагорная группа - это [1 + ,4,3,3], (






 =
= 



 ), порядок 192 и такой же, как симметрия #demitessractic : [3 1,1,1 ]. Эта группа выражается в конструкции тессеракта чередующейся из 16 ячеек .
), порядок 192 и такой же, как симметрия #demitessractic : [3 1,1,1 ]. Эта группа выражается в конструкции тессеракта чередующейся из 16 ячеек . 





 =
= 



 .
. - Группа [1 + ,4,(3,3) + ], (






 =
= 



 ), порядка 96 и то же, что и хиральная демитэссерактическая группа [3 1,1,1 ] + а также является коммутатором группы [4,3,3].
), порядка 96 и то же, что и хиральная демитэссерактическая группа [3 1,1,1 ] + а также является коммутатором группы [4,3,3].
- Группа [1 + ,4,(3,3) + ], (
- Высокоиндексной отражающей подгруппой является призматическая октаэдрическая симметрия , [4,3,2] (






 ), порядок 96, индекс подгруппы 4, (Дю Вал #44 (O/C 2 ;O/C 2 ) * , Конвей ± 1 / 24 [О×О].2). Усеченная кубическая призма имеет симметрию с диаграммой Кокстера.
), порядок 96, индекс подгруппы 4, (Дю Вал #44 (O/C 2 ;O/C 2 ) * , Конвей ± 1 / 24 [О×О].2). Усеченная кубическая призма имеет симметрию с диаграммой Кокстера. 





 а кубическая призма представляет собой конструкцию тессеракта с более низкой симметрией , так как
а кубическая призма представляет собой конструкцию тессеракта с более низкой симметрией , так как 





 .
. - Его киральная подгруппа — [4,3,2] + , (






 ), порядок 48, (Дю Вал № 26 (O/C 2 ; O/C 2 ), Конвей ± 1 / 24 [О×О]). Примером может служить курносая кубическая антипризма .
), порядок 48, (Дю Вал № 26 (O/C 2 ; O/C 2 ), Конвей ± 1 / 24 [О×О]). Примером может служить курносая кубическая антипризма . 





 , хотя сделать его единым невозможно.
, хотя сделать его единым невозможно. - Ионные подгруппы:
- [(3,4) + ,2], (






 ), порядок 48, (Дю Вал # 44b' (O/C 1 ;O/C 1 ) - * , Конвей + 1 / 24 [О×О].2 1 ). Плосконосая кубическая призма имеет симметрию с диаграммой Кокстера.
), порядок 48, (Дю Вал # 44b' (O/C 1 ;O/C 1 ) - * , Конвей + 1 / 24 [О×О].2 1 ). Плосконосая кубическая призма имеет симметрию с диаграммой Кокстера. 





 .
. - [(3,4) + ,2 + ], (






 ), порядок 24, (Дю Вал #44' (T/C 2 ;T/C 2 ) - * , Конвей + 1 / 12 [T×T].2 1 ).
), порядок 24, (Дю Вал #44' (T/C 2 ;T/C 2 ) - * , Конвей + 1 / 12 [T×T].2 1 ).
- [(3,4) + ,2 + ], (
- [4,3 + ,2], (






 ), порядок 48, (Дю Валь #39 (T/C 2 ;T/C 2 ) c * , Конвей ± 1 / 12 [T×T].2).
), порядок 48, (Дю Валь #39 (T/C 2 ;T/C 2 ) c * , Конвей ± 1 / 12 [T×T].2). - [4,3 + ,2,1 + ] = [4,3 + ,1] = [4,3 + ], (






 =
= 



 ), заказ 24, (Дю Валь #44" (Т/К 2 ;Т/К 2 ) * , Конвей + 1 / 12 [Т×Т].2 3 ). Это 3D пиритоэдрическая группа , [4,3 + ].
), заказ 24, (Дю Валь #44" (Т/К 2 ;Т/К 2 ) * , Конвей + 1 / 12 [Т×Т].2 3 ). Это 3D пиритоэдрическая группа , [4,3 + ]. - [3 + ,4,2 + ], (








 ), порядок 24, (Дю Валя № 21 (T/C 2 ; T/C 2 ), Конвей ± 1 / 12 [T×T]).
), порядок 24, (Дю Валя № 21 (T/C 2 ; T/C 2 ), Конвей ± 1 / 12 [T×T]).
- [4,3 + ,2,1 + ] = [4,3 + ,1] = [4,3 + ], (
- [3,4,2 + ], (






 ), порядок 48, (Дю Вал #39' (T/C 2 ;T/C 2 ) - * , Конвей ± 1 / 12 [T× T ].2).
), порядок 48, (Дю Вал #39' (T/C 2 ;T/C 2 ) - * , Конвей ± 1 / 12 [T× T ].2). - [4,(3,2) + ], (






 ), порядок 48, (Дю Валя № 40b' (O/C 1 ;O/C 1 ) - * , Конвей + 1 / 24 [O× O ].2 1 ).
), порядок 48, (Дю Валя № 40b' (O/C 1 ;O/C 1 ) - * , Конвей + 1 / 24 [O× O ].2 1 ).
- [(3,4) + ,2], (
- Полуподгруппа [4,3,2,1 + ] = [4,3,1] = [4,3], (






 =
= 



 ), порядок 48 (Дю Вал № 44b" (O/C 1 ;O/C 1 ) c * , Конвей + 1 / 24 [О×О].2 3 ). Она называется октаэдрической пирамидальной группой и представляет собой трехмерную октаэдрическую симметрию , [4,3]. Кубическая пирамида может иметь эту симметрию с символом Шлефли : ( ) ∨ {4,3}.
), порядок 48 (Дю Вал № 44b" (O/C 1 ;O/C 1 ) c * , Конвей + 1 / 24 [О×О].2 3 ). Она называется октаэдрической пирамидальной группой и представляет собой трехмерную октаэдрическую симметрию , [4,3]. Кубическая пирамида может иметь эту симметрию с символом Шлефли : ( ) ∨ {4,3}. 
[4,3], 



 , октаэдрическая пирамидальная группа изоморфна 3d- октаэдрической симметрии
, октаэдрическая пирамидальная группа изоморфна 3d- октаэдрической симметрии - Киральная полуподгруппа [(4,3) + ,2,1 + ] = [4,3,1] + = [4,3] + , (






 =
= 



 ), порядок 24 (Дю Вал № 26b' (O/C 1 ;O/C 1 ), Конвей + 1 / 24 [О×О]). Это 3D- хиральная октаэдрическая группа , [4,3] + . Плосконосая кубическая пирамида может иметь такую симметрию с символом Шлефли: ( ) ∨ sr{4,3}.
), порядок 24 (Дю Вал № 26b' (O/C 1 ;O/C 1 ), Конвей + 1 / 24 [О×О]). Это 3D- хиральная октаэдрическая группа , [4,3] + . Плосконосая кубическая пирамида может иметь такую симметрию с символом Шлефли: ( ) ∨ sr{4,3}.
- Киральная полуподгруппа [(4,3) + ,2,1 + ] = [4,3,1] + = [4,3] + , (
- Его киральная подгруппа — [4,3,2] + , (
- Другой отражающей подгруппой с высоким показателем отражения является призматическая тетраэдрическая симметрия , [3,3,2], (






 ), порядок 48, индекс подгруппы 8, (Du Val #40b" (O/C 1 ;O/C 1 ) * , Конвей + 1 / 24 [O× O ].2 3 ).
), порядок 48, индекс подгруппы 8, (Du Val #40b" (O/C 1 ;O/C 1 ) * , Конвей + 1 / 24 [O× O ].2 3 ). - Киральная подгруппа — это [3,3,2] + , (






 ), порядок 24, (Дю Валь #26b" (O/C 1 ;O/C 1 ), Конвей + 1 / 24 [О× О ]). Примером может служить курносая тетраэдрическая антипризма .
), порядок 24, (Дю Валь #26b" (O/C 1 ;O/C 1 ), Конвей + 1 / 24 [О× О ]). Примером может служить курносая тетраэдрическая антипризма . 





 , хотя сделать его единым невозможно.
, хотя сделать его единым невозможно. - Ионная подгруппа — это [(3,3) + ,2], (






 ), порядок 24, (Дю Валь #39b' (T/C 1 ;T/C 1 ) c * , Конвей + 1 / 12 [Т× Т ].2 3 ). Примером может служить курносая тетраэдрическая призма .
), порядок 24, (Дю Валь #39b' (T/C 1 ;T/C 1 ) c * , Конвей + 1 / 12 [Т× Т ].2 3 ). Примером может служить курносая тетраэдрическая призма . 





 .
. - Полуподгруппа — это [3,3,2,1 + ] = [3,3,1] = [3,3], (






 =
= 



 ), порядок 24, (Дю Валя #39b" (T/C 1 ;T/C 1 ) - * , Конвей + 1 / 12 [Т× Т ].2 1 ). Она называется тетраэдрической пирамидальной группой и представляет собой 3D- тетраэдрическую группу , [3,3]. Правильная тетраэдральная пирамида может иметь такую симметрию с символом Шлефли: ( ) ∨ {3,3}.
), порядок 24, (Дю Валя #39b" (T/C 1 ;T/C 1 ) - * , Конвей + 1 / 12 [Т× Т ].2 1 ). Она называется тетраэдрической пирамидальной группой и представляет собой 3D- тетраэдрическую группу , [3,3]. Правильная тетраэдральная пирамида может иметь такую симметрию с символом Шлефли: ( ) ∨ {3,3}. 
[3,3], 



 , тетраэдрическая пирамидальная группа изоморфна 3d- тетраэдрической симметрии
, тетраэдрическая пирамидальная группа изоморфна 3d- тетраэдрической симметрии - Киральная полуподгруппа [(3,3) + ,2,1 + ] = [3,3] + (






 =
= 



 ), порядок 12, (Дю Вал № 21b' (T/C 1 ;T/C 1 ), Конвей + 1 / 12 [Т×Т]). Это 3D хиральная тетраэдрическая группа , [3,3] + . с символом Шлефли: ( ) ∨ sr{3,3}. курносая тетраэдрическая пирамида Такую симметрию может иметь
), порядок 12, (Дю Вал № 21b' (T/C 1 ;T/C 1 ), Конвей + 1 / 12 [Т×Т]). Это 3D хиральная тетраэдрическая группа , [3,3] + . с символом Шлефли: ( ) ∨ sr{3,3}. курносая тетраэдрическая пирамида Такую симметрию может иметь
- Киральная полуподгруппа [(3,3) + ,2,1 + ] = [3,3] + (
- Киральная подгруппа — это [3,3,2] + , (
- Другая подгруппа радиальной отражающей способности с высоким индексом - [4,(3,3) * ], индекс 24, удаляет зеркала с двугранными углами порядка 3, создавая [2,2,2] (






 ), порядок 16. Остальные — [4,2,4] (
), порядок 16. Остальные — [4,2,4] ( 





 ), [4,2,2] (
), [4,2,2] ( 





 ), с индексами подгрупп 6 и 12, порядка 64 и 32. Эти группы являются нижними симметриями тессеракта : (
), с индексами подгрупп 6 и 12, порядка 64 и 32. Эти группы являются нижними симметриями тессеракта : ( 





 ), (
), ( 





 ), и (
), и ( 





 ). Эти группы обладают #дуопризматической симметрией .
). Эти группы обладают #дуопризматической симметрией .
- Хиральная гексадекагорная группа - [4,3,3] + , (
Икоситетрахорическая симметрия
[ редактировать ]- Икозитетрахорическая группа – F 4 , [3,4,3], (






 ), заказ 1152, (Дю Валь #45 (О/Т;О/Т) * , Конвей ± 1 / 2 [OxO].2), названный в честь 24-клеточного (икозитрахорон),
), заказ 1152, (Дю Валь #45 (О/Т;О/Т) * , Конвей ± 1 / 2 [OxO].2), названный в честь 24-клеточного (икозитрахорон), 





 . В этой симметрии имеется 24 зеркальные плоскости, которые можно разложить на два ортогональных набора по 12 зеркал с демитэссерактической симметрией [3]. 1,1,1 ] подгруппы, так как [3 * ,4,3] и [3,4,3 * ], как подгруппы индекса 6.
. В этой симметрии имеется 24 зеркальные плоскости, которые можно разложить на два ортогональных набора по 12 зеркал с демитэссерактической симметрией [3]. 1,1,1 ] подгруппы, так как [3 * ,4,3] и [3,4,3 * ], как подгруппы индекса 6. - Расширенная икоситетрахорная группа , Aut ( F 4 ), [[3,4,3]], (



 ) имеет заказ 2304, (Дю Валь #48 (O/O;O/O) * , Конвей ±[O×O].2).
) имеет заказ 2304, (Дю Валь #48 (O/O;O/O) * , Конвей ±[O×O].2). - Хиральная расширенная икоситетрахорная группа , [[3,4,3]] + , (



 ) имеет порядок 1152 (Дю Валя #25 (O/O;O/O), Конвей ±[OxO]). Эта группа представляет собой конструкцию omnisnub из 24 ячеек ,
) имеет порядок 1152 (Дю Валя #25 (O/O;O/O), Конвей ±[OxO]). Эта группа представляет собой конструкцию omnisnub из 24 ячеек , 


 , хотя сделать его единым невозможно.
, хотя сделать его единым невозможно.
- Хиральная расширенная икоситетрахорная группа , [[3,4,3]] + , (
- Ионные уменьшенные икоситетрахорические группы , [3 + ,4,3] и [3,4,3 + ], (






 или
или 





 ), заказ 576, (Дю Валь #43 (T/T;T/T) * , Конвей ±[T×T].2). Эта группа приводит к курносой 24-клеточной конструкции
), заказ 576, (Дю Валь #43 (T/T;T/T) * , Конвей ±[T×T].2). Эта группа приводит к курносой 24-клеточной конструкции 





 или
или 





 .
. - Двукратно уменьшенная икоситетрахорическая группа , [3 + ,4,3 + ] (двойное убавление можно показать пробелом в 4-ветви диаграммы:








 ), порядок 288, (Дю Валя #20 (T/T;T/T), Конвей ±[T×T]) — коммутант группы [3,4,3].
), порядок 288, (Дю Валя #20 (T/T;T/T), Конвей ±[T×T]) — коммутант группы [3,4,3]. - Его можно расширить как [[3 + ,4,3 + ]], (



 ) порядок 576, (Дю Вал № 23 (T/T;O/O), Конвей ±[OxT]).
) порядок 576, (Дю Вал № 23 (T/T;O/O), Конвей ±[OxT]).
- Его можно расширить как [[3 + ,4,3 + ]], (
- Двукратно уменьшенная икоситетрахорическая группа , [3 + ,4,3 + ] (двойное убавление можно показать пробелом в 4-ветви диаграммы:
- Хиральная икоситетрахорная группа - это [3,4,3] + , (






 ), порядок 576, (Дю Вал № 28 (O/T;O/T), Конвей ± 1 / 2 [O×O]).
), порядок 576, (Дю Вал № 28 (O/T;O/T), Конвей ± 1 / 2 [O×O]). - Расширенная хиральная икоситетрахорная группа , [[3,4,3] + ] имеет порядок 1152, (Дю Вал № 46 (O/T;O/T) — * , Конвей ± 1 / 2 [ОхО]. 2 ). Коксетер относит эту группу к абстрактной группе (4,8|2,3). [13]
- Расширенная икоситетрахорная группа , Aut ( F 4 ), [[3,4,3]], (
Демитэссерактическая симметрия
[ редактировать ]- Демитэссерактическая группа – D 4 , [3 1,1,1 ], [3,3 1,1 ] или [3,3,4,1 + ], (




 =
= 





 ), order 192, (Du Val #42 (T/V;T/V) − * , Конвей ± 1 / 3 [T× T ].2), названный в честь (демитесеракта) 4-полукубической конструкции 16-ячеечной клетки,
), order 192, (Du Val #42 (T/V;T/V) − * , Конвей ± 1 / 3 [T× T ].2), названный в честь (демитесеракта) 4-полукубической конструкции 16-ячеечной клетки, 





 или
или 



 . В этой группе симметрии 12 зеркал.
. В этой группе симметрии 12 зеркал. - Существует два типа расширенной симметрии путем добавления зеркал: <[3,3 1,1 ]> который становится [4,3,3] путем разделения фундаментальной области пополам зеркалом, с возможными 3 ориентациями; и полная расширенная группа [3[3 1,1,1 ]] становится [3,4,3].
- Киральная демитэссерактическая группа — это [3 1,1,1 ] + или [1 + ,4,(3,3) + ], (




 =
= 





 ), order 96, (Du Val #22 (T/V;T/V), Conway ± 1 / 3 [Т×Т]). Эта группа приводит к курносой 24-клеточной конструкции
), order 96, (Du Val #22 (T/V;T/V), Conway ± 1 / 3 [Т×Т]). Эта группа приводит к курносой 24-клеточной конструкции 



 =
= 





 .
.
Гексакосихорная симметрия
[ редактировать ] [5,3,3] + 72 порядка-5 витков |  [5,3,3] + 200 порядка-3 оборота |
 [5,3,3] + 450 порядка-2 оборота |  [5,3,3] + все вращения |
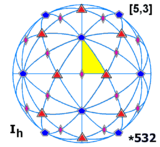 [5,3], |
- Гексакосихорная группа – H 4 , [5,3,3], (






 ), заказ 14400, (Дю Валь #50 (I/I;I/I) * , Конвей ±[I×I].2), названный в честь 600-клеточного (гексакосихорона),
), заказ 14400, (Дю Валь #50 (I/I;I/I) * , Конвей ±[I×I].2), названный в честь 600-клеточного (гексакосихорона), 





 . Ее также иногда называют гипер-икосаэдрической группой из-за расширения трехмерной икосаэдрической группы [5,3] и гекатоникосахорной группы или додекаконтахорной группы из 120-клеточной группы .
. Ее также иногда называют гипер-икосаэдрической группой из-за расширения трехмерной икосаэдрической группы [5,3] и гекатоникосахорной группы или додекаконтахорной группы из 120-клеточной группы . 





 .
. - Хиральная гексакосихорная группа - это [5,3,3] + , (






 ), порядок 7200, (Дю Валя #30 (I/I;I/I), Конвей ±[I×I]). конструкцию Эта группа представляет собой курносую 120-ячеечную ,
), порядок 7200, (Дю Валя #30 (I/I;I/I), Конвей ±[I×I]). конструкцию Эта группа представляет собой курносую 120-ячеечную , 





 , хотя сделать его единым невозможно.
, хотя сделать его единым невозможно. - Подгруппа отражающей способности с высоким показателем отражения — это призматическая икосаэдрическая симметрия , [5,3,2], (






 ), порядок 240, индекс подгруппы 60, (Дю Валя #49 (I/C 2 ;I/C 2 ) * , Конвей ± 1 / 60 [IxI].2).
), порядок 240, индекс подгруппы 60, (Дю Валя #49 (I/C 2 ;I/C 2 ) * , Конвей ± 1 / 60 [IxI].2). - Его киральная подгруппа - [5,3,2] + , (






 ), порядок 120, (Дю Валя #31 (I/C 2 ; I/C 2 ), Конвей ± 1 / 60 [IxI]). Эта группа представляет собой конструкцию курносой додекаэдрической антипризмы .
), порядок 120, (Дю Валя #31 (I/C 2 ; I/C 2 ), Конвей ± 1 / 60 [IxI]). Эта группа представляет собой конструкцию курносой додекаэдрической антипризмы . 





 , хотя его нельзя сделать однородным.
, хотя его нельзя сделать однородным. - Ионная подгруппа — это [(5,3) + ,2], (






 ), порядок 120, (Дю Валь № 49' (I/C 1 ;I/C 1 ) * , Конвей + 1 / 60 [IxI].2 1 ). Эта группа представляет собой конструкцию курносой додекаэдрической призмы ,
), порядок 120, (Дю Валь № 49' (I/C 1 ;I/C 1 ) * , Конвей + 1 / 60 [IxI].2 1 ). Эта группа представляет собой конструкцию курносой додекаэдрической призмы , 





 .
. - Полуподгруппа — это [5,3,2,1 + ] = [5,3,1] = [5,3], (






 =
= 



 ), порядок 120, (Дю Валя #49" (I/C 1 ;I/C 1 ) - * , Конвей + 1 / 60 [IxI].2 3 ). Она называется икосаэдрической пирамидальной группой и представляет собой трехмерную икосаэдрическую группу , [5,3]. Правильная додекаэдрическая пирамида может иметь такую симметрию с символом Шлефли : ( ) ∨ {5,3}.
), порядок 120, (Дю Валя #49" (I/C 1 ;I/C 1 ) - * , Конвей + 1 / 60 [IxI].2 3 ). Она называется икосаэдрической пирамидальной группой и представляет собой трехмерную икосаэдрическую группу , [5,3]. Правильная додекаэдрическая пирамида может иметь такую симметрию с символом Шлефли : ( ) ∨ {5,3}. - Киральная полуподгруппа — это [(5,3) + ,2,1 + ] = [5,3,1] + = [5,3] + , (






 =
= 



 ), порядок 60, (Дю Валь #31' (I/C 1 ;I/C 1 ), Конвей + 1 / 60 [IxI]). Это 3D- хиральная группа икосаэдра , [5,3] + . может Плоско-додекаэдральная пирамида иметь такую симметрию с символом Шлефли : ( ) ∨ sr{5,3}.
), порядок 60, (Дю Валь #31' (I/C 1 ;I/C 1 ), Конвей + 1 / 60 [IxI]). Это 3D- хиральная группа икосаэдра , [5,3] + . может Плоско-додекаэдральная пирамида иметь такую симметрию с символом Шлефли : ( ) ∨ sr{5,3}.
- Киральная полуподгруппа — это [(5,3) + ,2,1 + ] = [5,3,1] + = [5,3] + , (
- Его киральная подгруппа - [5,3,2] + , (
- Хиральная гексакосихорная группа - это [5,3,3] + , (
Дуопризматическая симметрия
[ редактировать ]- Дуопризматические группы – [p,2,q], (






 ), порядка 4 pq , существуют для всех 2 ⩽ p , q < ∞. В этой симметрии существуют зеркала p + q, которые тривиально разлагаются на два ортогональных набора зеркал p и q двугранной симметрии : [p] и [q].
), порядка 4 pq , существуют для всех 2 ⩽ p , q < ∞. В этой симметрии существуют зеркала p + q, которые тривиально разлагаются на два ортогональных набора зеркал p и q двугранной симметрии : [p] и [q]. - Киральная подгруппа — это [p,2,p] + ,(






 ), заказывайте 2 шт . Его можно удвоить как [[2p,2,2p] + ].
), заказывайте 2 шт . Его можно удвоить как [[2p,2,2p] + ]. - Если p и q равны, [p,2,p], (






 ), симметрию можно удвоить как [[p,2,p]], (
), симметрию можно удвоить как [[p,2,p]], ( 



 ).
). - Удвоение: [[2 + ,2,п + ]], (




 ), [[2p,2 + ,2p]], [[2p + ,2 + ,2р + ]].
), [[2p,2 + ,2p]], [[2p + ,2 + ,2р + ]].
- Удвоение: [[2 + ,2,п + ]], (
- [p,2,∞], (






 ), он представляет собой группы линий в трехмерном пространстве,
), он представляет собой группы линий в трехмерном пространстве, - [∞,2,∞], (






 ) он представляет собой симметрию евклидовой плоскости с двумя наборами параллельных зеркал и прямоугольной областью ( орбифолд *2222).
) он представляет собой симметрию евклидовой плоскости с двумя наборами параллельных зеркал и прямоугольной областью ( орбифолд *2222). - Подгруппы включают: [p + ,2,q], (






 ), [p,2,q + ], (
), [p,2,q + ], ( 





 ), [п + ,2,д + ], (
), [п + ,2,д + ], ( 





 ).
). - И для четных значений: [2p,2 + ,2q], (








 ), [2p,2 + ,2к + ], (
), [2p,2 + ,2к + ], ( 







 ), [(п,2) + ,2q], (
), [(п,2) + ,2q], ( 







 ), [2p,(2,q) + ], (
), [2p,(2,q) + ], ( 







 ), [(п,2) + ,2к + ], (
), [(п,2) + ,2к + ], ( 







 ), [2п + ,(2,q) + ], (
), [2п + ,(2,q) + ], ( 







 ), [2п + ,2 + ,2к + ], (
), [2п + ,2 + ,2к + ], ( 







 ), и подгруппа коммунляторов, индекс 16, [2p + ,2 + ,2к + ] + , (
), и подгруппа коммунляторов, индекс 16, [2p + ,2 + ,2к + ] + , ( 









 ).
).
- Киральная подгруппа — это [p,2,p] + ,(
- Дигональная дуопризматическая группа – [2,2,2], (






 ), порядок 16.
), порядок 16. - Киральная подгруппа — это [2,2,2] + , (






 ), порядок 8.
), порядок 8. - Расширенный [[2,2,2]], (


 ), порядок 32. Дуопризма 4-4 имеет расширенную симметрию,
), порядок 32. Дуопризма 4-4 имеет расширенную симметрию, 





 .
. - Киральная расширенная группа — это [[2,2,2]] + , заказ 16.
- Расширенная киральная подгруппа — это [[2,2,2] + ], порядок 16, с роторно-отражательными генераторами. Она изоморфна абстрактной группе (4,4|2,2).
- Другие расширенные [(3,3)[2,2,2]]=[4,3,3], порядок 384, #Гексадекахорная симметрия . Тессеракт т.к. обладает такой симметрией,






 или
или 





 .
. - Ионные уменьшенные подгруппы - это [2 + ,2,2], порядок 8.
- Двукратно уменьшенная подгруппа — это [2 + ,2,2 + ], порядок 4.
- Расширено как [[2 + ,2,2 + ]], порядок 8.
- Подгруппы роторного отражения [2 + ,2 + ,2], [2,2 + ,2 + ], [2 + ,(2,2) + ], [(2,2) + ,2 + ] порядок 4.
- Тройная уменьшенная подгруппа — это [2 + ,2 + ,2 + ], (






 ), порядок 2. Это 2-кратное двойное вращение и 4D центральная инверсия .
), порядок 2. Это 2-кратное двойное вращение и 4D центральная инверсия .
- Двукратно уменьшенная подгруппа — это [2 + ,2,2 + ], порядок 4.
- Половина подгруппы — [1 + ,2,2,2]=[1,2,2], порядок 8.
- Киральная подгруппа — это [2,2,2] + , (
- Треугольная дуопризматическая группа – [3,2,3],






 , заказ 36.
, заказ 36. - Киральная подгруппа — это [3,2,3] + , заказ 18.
- Расширенный [[3,2,3]], порядок 72. Дуопризма 3-3 имеет расширенную симметрию:






 .
. - Киральная расширенная группа — это [[3,2,3]] + , заказ 36.
- Расширенная киральная подгруппа — это [[3,2,3] + ], порядок 36, с роторно-отражательными генераторами. Она изоморфна абстрактной группе (4,4|2,3).
- Другие расширенные [[3],2,3], [3,2,[3]] порядка 72 изоморфны [6,2,3] и [3,2,6].
- И 3,2,3 , порядка 144 , и изоморфен [6,2,6].
- И [[[3]],2,[3]]], порядка 288, изоморфны [[6,2,6]]. Дуопризма 6–6 обладает такой симметрией, так как






 или
или 





 .
. - Ионные уменьшенные подгруппы - это [3 + ,2,3], [3,2,3 + ], порядок 18.
- Двукратно уменьшенная подгруппа — это [3 + ,2,3 + ], порядок 9.
- Расширено как [[3 + ,2,3 + ]], порядок 18.
- Двукратно уменьшенная подгруппа — это [3 + ,2,3 + ], порядок 9.
- Подгруппа с высоким индексом - это [3,2] , порядок 12, индекс 3, которая изоморфна диэдральной симметрии в трехмерной группе, [3,2], D 3h .
- [3,2] + , заказ 6
- Квадратная дуопризматическая группа – [4,2,4],






 , заказ 64.
, заказ 64. - Киральная подгруппа — это [4,2,4] + , заказ 32.
- Расширенный [[4,2,4]], порядок 128. Дуопризма 4–4 имеет расширенную симметрию:






 .
. - Киральная расширенная группа — это [[4,2,4]] + , заказ 64.
- Расширенная киральная подгруппа — это [[4,2,4] + ], порядок 64, с роторно-отражательными генераторами. Она изоморфна абстрактной группе (4,4|2,4).
- Остальные расширенные [[4],2,4], [4,2,[4]] порядка 128 изоморфны [8,2,4] и [4,2,8]. Дуопризма 4–8 обладает такой симметрией, так как






 или
или 





 .
. - И 4,2,4 , порядка 256 , и изоморфен [8,2,8].
- И [[[4]],2,[4]]] порядка 512, изоморфный [[8,2,8]]. Дуопризма 8–8 обладает такой симметрией, так как






 или
или 





 .
. - Ионные уменьшенные подгруппы - это [4 + ,2,4], [4,2,4 + ], порядок 32.
- Двукратно уменьшенная подгруппа — это [4 + ,2,4 + ], порядок 16.
- Расширено как [[4 + ,2,4 + ]], порядок 32.
- Подгруппы роторного отражения [4 + ,2 + ,4], [4,2 + ,4 + ], [4 + ,(2,4) + ], [(4,2) + ,4 + ], (






 ,
, 





 ,
, 





 ,
, 





 ) заказ 16.
) заказ 16. - Тройная уменьшенная подгруппа — это [4 + ,2 + ,4 + ], (






 ), порядок 8.
), порядок 8.
- Двукратно уменьшенная подгруппа — это [4 + ,2,4 + ], порядок 16.
- Полуподгруппы - это [1 + ,4,2,4]=[2,2,4], (






 ), [4,2,4,1 + ]=[4,2,2], (
), [4,2,4,1 + ]=[4,2,2], ( 





 ), заказ 32.
), заказ 32. - [1 + ,4,2,4] + =[2,2,4] + , (






 ), [4,2,4,1 + ] + =[4,2,2] + , (
), [4,2,4,1 + ] + =[4,2,2] + , ( 





 ), порядок 16.
), порядок 16.
- [1 + ,4,2,4] + =[2,2,4] + , (
- Половина подгруппы снова [1 + ,4,2,4,1 + ]=[2,2,2], (






 ), порядок 16.
), порядок 16. - [1 + ,4,2,4,1 + ] + = [1 + ,4,2 + ,4,1 + ] = [2,2,2] + , (






 ) заказать 8
) заказать 8
- [1 + ,4,2,4,1 + ] + = [1 + ,4,2 + ,4,1 + ] = [2,2,2] + , (
Краткое описание некоторых четырехмерных точечных групп
[ редактировать ]Это краткое изложение 4-мерных точечных групп в обозначениях Кокстера . Из них 227 являются кристаллографическими точечными группами (при определенных значениях p и q). [14] [ который? ] (nc) приведен для некристаллографических групп. Некоторые кристаллографические группы [ который? ] индексировать свои заказы (order.index) по их абстрактной групповой структуре. [15]
| Конечные группы |
|---|
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Херли, AC; Дирак, ПАМ (1951). «Группы конечных вращений и классы кристаллов в четырех измерениях» . Математические труды Кембриджского философского общества . 47 (4): 650–661. Бибкод : 1951PCPS...47..650H . дои : 10.1017/S0305004100027109 . S2CID 122468489 .
- ^ http://met.iisc.ernet.in/~lord/webfiles/Alan/CV25.pdf [ пустой URL PDF ]
- ^ Мозжимас, Ян; Солецкий, Анджей (1975). «Группы точек R4». Доклады по математической физике . 7 (3): 363–394. Бибкод : 1975РпМП....7..363М . дои : 10.1016/0034-4877(75)90040-3 .
- ^ Браун, Х; Бюлов, Р; Нойбюзер, Дж; Вондраччек, Х; Зассенхаус, Х (1978). Кристаллографические группы четырехмерного пространства (PDF) . Уайли .
- ^ Уорнер, НП (1982). «Группы симметрии регулярных мозаик S2 и S3». Труды Лондонского королевского общества. Серия А, Математические и физические науки . 383 (1785): 379–398. Бибкод : 1982RSPSA.383..379W . дои : 10.1098/rspa.1982.0136 . JSTOR 2397289 . S2CID 119786906 .
- ^ Коксетер, Регулярные и полуправильные многогранники II , 1985, 2.2 Четырехмерные группы отражений , 2.3 Подгруппы малого индекса
- ^ Коксетер , Правильные многогранники , §12.6 Число отражений, уравнение 12.61
- ^ Патрик Дю Валь, Гомографии, кватернионы и вращения , Оксфордские математические монографии, Clarendon Press , Оксфорд , 1964.
- ^ Конвей и Смит, О кватернионах и октонионах , 2003 г., глава 4, раздел 4.4. Обозначения Коксетера для многогранных групп.
- ^ «Выпуклые и абстрактные многогранники», Программа и рефераты, Массачусетский технологический институт, 2005 г.
- ^ Джонсон (2015), Глава 11, Раздел 11.5 Сферические группы Кокстера
- ^ Что такое многогранники? , с греческими цифровыми префиксами
- ^ Перейти обратно: а б Коксетер, Абстрактные группы G м;н;п , (1939)
- ^ Вайгель, Д.; Фан, Т.; Вейсейр, Р. (1987). «Кристаллография, геометрия и физика в высших измерениях. III. Геометрические символы для 227 кристаллографических точечных групп в четырехмерном пространстве». Акта Кристаллогр . A43 (3): 294. Бибкод : 1987AcCrA..43..294W . дои : 10.1107/S0108767387099367 .
- ^ Коксетер, Правильные и полуправильные многогранники II (1985)
- HSM Coxeter, Правильные многогранники , 3-е издание, Дувр, Нью-Йорк, 1973 г.
- Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380–407, МР 2,10]
- (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559–591]
- (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3–45]
- HSM Coxeter и WOJ Moser. Генераторы и отношения для дискретных групп. 4-е изд., Springer-Verlag. Нью-Йорк. 1980 стр.92, стр.122.
- Джон .Х. Конвей и Гай MJT : Четырехмерные архимедовы многогранники , Материалы коллоквиума по выпуклости в Копенгагене, стр. 38 и 39, 1965 г.
- Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.
- Н. В. Джонсон : Геометрии и трансформации (2018) ISBN 978-1-107-10340-5 Глава 11: Группы конечной симметрии , 11.5 Сферические группы Кокстера , стр. 11.5. 249
- Джон Х. Конвей и Дерек А. Смит, О кватернионах и октонионах , 2003 г., ISBN 978-1-56881-134-5
- Джон Х. Конвей, Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (глава 26)
Внешние ссылки
[ редактировать ]- Вайсштейн, Эрик В. «Равномерный полихорон» . Математический мир .
- Клитцинг, Ричард. «4D однородные многогранники» .





