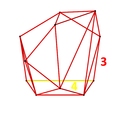
Ранцинированные 24 клетки
 24-ячеечный |  Ранцинированный 24-клеточный |
 Runcitусеченный 24-клеточный |  Всеусеченный 24-клеточный (Runcicantiусеченный, 24-клеточный) |
| Ортогональные проекции в F 4 плоскости Кокстера | |
|---|---|
В четырехмерной геометрии многогранник укороченный 24-клеточный представляет собой выпуклый однородный 4-мерный многогранник , являющийся укорочением (усечением 3-го порядка) обычного 24-клеточного .
Существует 3 уникальные степени усечения 24-клеток, включая перестановки, усечения и кантелляции.
Ранцинированный 24-клеточный
[ редактировать ]| Ранцинированный 24-клеточный | ||
| Тип | Равномерный 4-многогранник | |
| Символ Шлефли | т 0,3 {3,4,3} | |
| Диаграмма Кокстера | ||
| Клетки | 240 | 48 3.3.3.3 192 3.4.4 |
| Лица | 672 | 384{3} 288{4} |
| Края | 576 | |
| Вершины | 144 | |
| Вершинная фигура |  вытянутая квадратная антипризма | |
| Группа симметрии | Аут (F 4 ), [[3,4,3]], заказ 2304 | |
| Характеристики | выпуклый , транзитивный по ребру | |
| Единый индекс | 25 26 27 | |

В геометрии усеченный , 24-клеточный или малый призматотетраконтоктахорон представляет собой однородный 4-многогранник ограниченный 48 октаэдрами и 192 треугольными призмами . Октаэдрические ячейки соответствуют ячейкам 24-клетки и ее двойника.
Э. Л. Эльте идентифицировал его в 1912 г. как полуправильный многогранник.
Альтернативные названия
[ редактировать ]- Обрезанные 24 клетки ( Норман В. Джонсон )
- Ранцинированный икоситетрахорон
- Скругленный полиоктаэдр
- Маленький призматотетраконтоктахорон (спик) (Джонатан Бауэрс)
Координаты
[ редактировать ]Декартовы координаты прорезанных 24 ячеек с длиной ребра 2 задаются всеми перестановками знаков и координат:
- (0, 0, √ 2 , 2+ √ 2 )
- (1, 1, 1+ √ 2 , 1+ √ 2 )
Перестановки второго набора координат совпадают с вершинами вписанного кантеллированного тессеракта .
Прогнозы
[ редактировать ]| Самолет Коксетера | FF4 | Б 4 |
|---|---|---|
| График |  |  |
| Двугранная симметрия | [[12]] = [24] | [8] |
| Самолет Коксетера | Б3 / А2 | Б2 / А3 |
| График |  |  |
| Двугранная симметрия | [6] | [[4]] = [8] |
| 3D перспективные проекции | ||
|---|---|---|
 Диаграмма Шлегеля с центром в октаэдре, показаны октаэдры. |  Перспективная проекция 24-клеточной структуры в трех измерениях с центром в октаэдрической ячейке. Вращение происходит только для трехмерного изображения, чтобы показать его структуру, а не вращение в четырехмерном пространстве. Пятнадцать октаэдрических ячеек, обращенных к точке зрения 4D, показаны здесь красным. Промежутки между ними заполнены каркасом из треугольных призм. |  Стереографическая проекция с 24 из 48 октаэдрических ячеек. |
Связанный правильный косой многогранник
[ редактировать ]Правильный косой многогранник {4,8|3} существует в 4-мерном пространстве с 8 квадратами вокруг каждой вершины, в зигзагообразной неплоской вершинной фигуре. Эти квадратные грани можно увидеть на 24-ячеечной структуре, использующей все 576 ребер и 288 вершин. 384 треугольные грани сморщенной 24-клеточной клетки можно рассматривать как удаленные. Двойственный правильный косой многогранник {8,4|3} аналогичным образом связан с восьмиугольными гранями усеченного побитно 24-ячеечного .
Runcitусеченный 24-клеточный
[ редактировать ]| Runcitусеченный 24-клеточный | ||
| Тип | Равномерный 4-многогранник | |
| Символ Шлефли | т 0,1,3 {3,4,3} с 2,3 {3,4,3} | |
| Диаграмма Кокстера | ||
| Клетки | 240 | 24 4.6.6 96 4.4.6 96 3.4.4 24 3.4.4.4 |
| Лица | 1104 | 192{3} 720{4} 192{6} |
| Края | 1440 | |
| Вершины | 576 | |
| Вершинная фигура |  Трапециевидная пирамида | |
| Группа симметрии | F 4 , [3,4,3], порядок 1152 | |
| Характеристики | выпуклый | |
| Единый индекс | 28 29 30 | |

Укороченный 24-клеточный или призматоромбатированный икоситетрахорон представляет собой однородный 4-мерный многогранник, полученный из 24-клеточного . Он ограничен 24 усеченными октаэдрами , соответствующими ячейкам 24-клеточного , 24 ромбокубооктаэдрами , соответствующими ячейкам двойного 24-клеточного, 96 треугольными призмами и 96 шестиугольными призмами .
Координаты
[ редактировать ]Декартовы координаты усеченной 24-ячейки с центром в начале координат и длиной ребра 2 задаются всеми перестановками координат и знаком:
- (0, √ 2 , 2 √ 2 , 2+3 √ 2 )
- (1, 1+ √ 2 , 1+2 √ 2 , 1+3 √ 2 )
Перестановки второго набора координат дают вершины вписанного всеусеченного тессеракта .
Двойная конфигурация имеет координаты, сгенерированные из всех перестановок и знаков:
- (1,1,1+ √ 2 ,5+ √ 2 )
- (1,3,3+ √ 2 ,3+ √ 2 )
- (2,2,2+ √ 2 ,4+ √ 2 )
Прогнозы
[ редактировать ]| Самолет Коксетера | FF4 | |
|---|---|---|
| График |  | |
| Двугранная симметрия | [12] | |
| Самолет Коксетера | Б3 ) /А2 ( а | Б 3 / А 2 (б) |
| График |  |  |
| Двугранная симметрия | [6] | [6] |
| Самолет Коксетера | Б 4 | Б2 / А3 |
| График |  |  |
| Двугранная симметрия | [8] | [4] |
 Диаграмма Шлегеля с центром в ромбокубооктаэдре показаны только треугольные призмы |
Рансикантический курносый 24-клеточный
[ редактировать ]Полусимметричная конструкция из 24-клеточных ранцикантеллированных клеток, как ![]()
![]()
![]()
![]()
![]()
![]()
![]() , также называемый рунцикантическим курносым 24-клеточным , как
, также называемый рунцикантическим курносым 24-клеточным , как ![]()
![]()
![]()
![]()
![]()
![]()
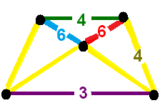
![]() , имеет идентичную геометрию, но его треугольные грани дополнительно подразделены. Как и курносый 24-клеточный, он обладает симметрией [3 + ,4,3], порядок 576. Усеченно-усеченная 24-клетка имеет 192 одинаковых шестиугольных грани, а уранцикантическая курносая 24-клетка имеет 2 конструктивных набора по 96 шестиугольников. Разницу можно увидеть на фигурах вершин :
, имеет идентичную геометрию, но его треугольные грани дополнительно подразделены. Как и курносый 24-клеточный, он обладает симметрией [3 + ,4,3], порядок 576. Усеченно-усеченная 24-клетка имеет 192 одинаковых шестиугольных грани, а уранцикантическая курносая 24-клетка имеет 2 конструктивных набора по 96 шестиугольников. Разницу можно увидеть на фигурах вершин :
 |  |
Руничич курносый 24-клеточный
[ редактировать ]| Руничич курносый 24-клеточный | ||
|---|---|---|
| Символ Шлефли | с 3 {3,4,3} | |
| Диаграмма Кокстера | ||
| Клетки | 240 | 24 {3,5} 24 т{3,3} 96 (4.4.3) 96 трикуп |
| Лица | 960 | 576 {3} 288 {4} 96 {6} |
| Края | 1008 | |
| Вершины | 288 | |
| Вершинная фигура |  | |
| Группа симметрии | [3 + ,4,3], порядок 576 | |
| Характеристики | выпуклый | |
Родственный 4-многогранник — курносый рунический 24-клеточный или призматоромбиснуб икоситетрахорон , s 3 {3,4,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() . Он не однороден, но вершинно-транзитивен и имеет все грани правильных многоугольников. Он состоит из 24 икосаэдров , 24 усеченных тетраэдров , 96 треугольных призм и 96 треугольных куполов в промежутках, всего 240 ячеек, 960 граней, 1008 ребер и 288 вершин. Как и курносый 24-клеточный , он обладает симметрией [3 + ,4,3], порядок 576. [1]
. Он не однороден, но вершинно-транзитивен и имеет все грани правильных многоугольников. Он состоит из 24 икосаэдров , 24 усеченных тетраэдров , 96 треугольных призм и 96 треугольных куполов в промежутках, всего 240 ячеек, 960 граней, 1008 ребер и 288 вершин. Как и курносый 24-клеточный , он обладает симметрией [3 + ,4,3], порядок 576. [1]
Вершинная фигура содержит один икосаэдр, две треугольные призмы, один усеченный тетраэдр и 3 треугольных купола.
| Орфографические проекции | Сеть | ||
|---|---|---|---|
 |  |  |  |
Всеусеченный 24-клеточный
[ редактировать ]| Всеусеченный 24-клеточный | ||
| Тип | Равномерный 4-многогранник | |
| Символ Шлефли | т 0,1,2,3 {3,4,3} | |
| Диаграмма Кокстера | ||
| Клетки | 240 | 48 (4.6.8) 192 (4.4.6) |
| Лица | 1392 | 864 {4} 384 {6} 144 {8} |
| Края | 2304 | |
| Вершины | 1152 | |
| Вершинная фигура |  Филлический дисфеноид | |
| Группа симметрии | Аут (F 4 ), [[3,4,3]], заказ 2304 | |
| Характеристики | выпуклый | |
| Единый индекс | 29 30 31 | |
Всеусеченный 24-клеточный или большой призматотетраконтоктахорон представляет собой однородный 4-мерный многогранник, полученный из 24-клеточного . Он состоит из 1152 вершин, 2304 ребер и 1392 граней (864 квадрата, 384 шестиугольников и 144 восьмиугольников). Он имеет 240 ячеек: 48 усеченных кубооктаэдров , 192 шестиугольные призмы . Каждая вершина содержит четыре ячейки филлической дисфеноидальной вершинной фигуры : две шестиугольные призмы и два усеченных кубооктаэдра .
Структура
[ редактировать ]48 усеченных кубооктаэдрических ячеек соединены друг с другом восьмиугольными гранями. Их можно сгруппировать в две группы по 24 в каждой, что соответствует ячейкам 24-ячейки и ее двойника. Промежутки между ними заполнены сетью из 192 шестиугольных призм, соединенных друг с другом через чередующиеся квадратные грани в чередующейся ориентации, а с усеченными кубооктаэдрами через их шестиугольные грани и оставшиеся квадратные грани.
Координаты
[ редактировать ]Все декартовы координаты всеусеченной 24-ячейки с длиной ребра 2 представляют собой перестановки координат и знака:
- (1, 1+ √ 2 , 1+2 √ 2 , 5+3 √ 2 )
- (1, 3+ √ 2 , 3+2 √ 2 , 3+3 √ 2 )
- (2, 2+ √ 2 , 2+2 √ 2 , 4+3 √ 2 )
Изображения
[ редактировать ]| Самолет Коксетера | FF4 | Б 4 |
|---|---|---|
| График |  |  |
| Двугранная симметрия | [[12]] = [24] | [8] |
| Самолет Коксетера | Б3 / А2 | Б2 / А3 |
| График |  |  |
| Двугранная симметрия | [6] | [[4]] = [8] |
| 3D перспективные проекции | |
|---|---|
 Диаграмма Шлегеля |  Перспективная проекция в 3D с центром в усеченном кубооктаэдре. Ближайшая к четырехмерной точке зрения большая ромбокубооктаэдрическая ячейка показана красным, а шесть окружающих ее больших ромбокубооктаэдров — желтым. Двенадцать шестиугольных призм, имеющих квадратную грань с ближайшей ячейкой, а шестиугольные грани с желтыми ячейками показаны синим цветом. Остальные ячейки показаны зеленым цветом. Ячейки, лежащие на дальней стороне многогранника с точки зрения 4D, были исключены для ясности. |
 Всеусеченный 24-клеточный |  От двух до всеусеченных 24 ячеек |
Связанные многогранники
[ редактировать ]Неоднородные варианты с симметрией [3,4,3] и двумя типами усеченных кубооктаэдров можно удвоить, поместив два типа усеченных кубооктаэдров друг на друга, чтобы получить неоднородный полихорон с 48 усеченными кубооктаэдрами , 144 восьмиугольными призмами (как дитетрагональные трапезопризмы), 192 шестиугольные призмы двух видов , 864 прямоугольных трапеции (288 с D 2d симметрией и 576 с симметрией C 2v ) и 2304 вершины. Ее вершинная фигура представляет собой неправильную треугольную бипирамиду .
Этот полихорон затем можно чередовать, чтобы получить другой неоднородный полихорон с 48 курносыми кубами , 144 квадратными антипризмами , 192 октаэдрами (как треугольные антипризмы), тремя видами тетраэдров 2016 года (288 тетрагональных дисфеноидов, 576 филлических дисфеноидов и 1152 неправильных тетраэдров) и 1152 вершины. Он имеет симметрию [[3,4,3] + ], приказ 1152.
Полный курносый 24-элементный
[ редактировать ]
Равномерный курносый 24-элементный элемент полувзносым 24-элементным назвал Джон Хортон Конвей с помощью диаграммы Коксетера. ![]()
![]()
![]()
![]()
![]()
![]()
![]() внутри семейства F 4 он является полным курносым или омниснубом , хотя в семействе D 4 , поскольку
внутри семейства F 4 он является полным курносым или омниснубом , хотя в семействе D 4 , поскольку ![]()
![]()
![]()
![]()
![]() .
.
Напротив, полностью курносую 24-элементную или несимметричную 24-элементную , определяемую как чередование всеусеченных 24-элементных, нельзя сделать однородным, но можно представить диаграмму Коксетера. ![]()
![]()
![]()
![]()
![]()
![]()
![]() и симметрия [[3,4,3]] + , порядка 1152 и построен из 48 курносых кубов , 192 октаэдров и 576 тетраэдров , заполняющих пробелы в удаленных вершинах. Его вершинная фигура содержит 4 тетраэдра, 2 октаэдра и 2 курносых куба. Он имеет 816 ячеек, 2832 грани, 2592 ребра и 576 вершин. [2]
и симметрия [[3,4,3]] + , порядка 1152 и построен из 48 курносых кубов , 192 октаэдров и 576 тетраэдров , заполняющих пробелы в удаленных вершинах. Его вершинная фигура содержит 4 тетраэдра, 2 октаэдра и 2 курносых куба. Он имеет 816 ячеек, 2832 грани, 2592 ребра и 576 вершин. [2]
Связанные многогранники
[ редактировать ]| 24-клеточные семейные многогранники |
|---|
Примечания
[ редактировать ]Ссылки
[ редактировать ]- Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
- (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
- (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
- Дж. Х. Конвей и М. Дж. Т. Гай : Четырехмерные архимедовы многогранники , материалы коллоквиума по выпуклости в Копенгагене, стр. 38 и 39, 1965 г.
- Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.
- Четырехмерные архимедовы многогранники (немецкий язык), Марко Мёллер, 2004 г. Кандидатская диссертация [1] m58 m59 m53
- 3. Выпуклая равномерная полихора на основе икоситетрахорона (24-клеточного) , Георгий Ольшевский.
- Клитцинг, Ричард. «4D однородные многогранники (полихора)» . x3o4o3x - спик, x3x4o3x - прико, s3s4o3x - присси, x3x4x3x - гиппик