Рансинация
Эта статья включает список литературы , связанную литературу или внешние ссылки , но ее источники остаются неясными, поскольку в ней отсутствуют встроенные цитаты . ( Март 2015 г. ) |

В геометрии правильный прогонка — это операция, которая разрезает многогранник (или сот ) одновременно по граням, ребрам и вершинам, создавая новые грани вместо исходных центров граней, ребер и вершин. [ нужна ссылка ]
Это операция усечения более высокого порядка, следующая за кантелляцией и усечением .
Он представлен расширенным символом Шлефли t 0,3 {p,q,...}. Эта операция существует только для 4-многогранников {p,q,r} или выше.
Эта операция является дуально-симметричной для правильных однородных 4-многогранников и 3-мерных выпуклых однородных сот .
Для правильного 4-многогранника {p,q,r} исходные ячейки {p,q} остаются, но становятся разделенными. Промежутки на разделенных гранях становятся p -угольными призмами . Промежутки между разделенными краями становятся r -угольными призмами. Промежутки между разделенными вершинами становятся ячейками {r,q}. Фигура вершины правильного 4-многогранника {p,q,r} представляет собой q -угольную антипризму (называемую антиподием, если p и r различны).
Для правильных 4-многогранников/сот эта операция также называется расширением Алисии Буль Стотт , как предполагалось путем перемещения ячеек правильной формы от центра и заполнения новых граней в промежутках для каждой открытой вершины и ребра.
Сморщенные 4-многогранники/соты образуют:
| Символ Шлефли Диаграмма Кокстера | Имя | Вершинная фигура | Изображение |
|---|---|---|---|
| Однородные 4-многогранники | |||
| т 0,3 {3,3,3} | Ранцинированный 5-клеточный |  |  |
| т 0,3 {3,3,4} | Ранцинированный 16-клеточный (То же самое, что и 8-клеточный ранцинированный ) |  |   |
| т 0,3 {3,4,3} | Ранцинированный 24-клеточный |  |  |
| т 0,3 {3,3,5} | Ранцинированный, 120 ячеек (То же самое, что и 600-ячеечная версия ) |  |  |
| Евклидовы выпуклые однородные соты | |||
| т 0,3 {4,3,4} | Стертые кубические соты (То же, что и кубические соты ) | 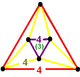 |  |
| Гиперболические однородные соты | |||
| т 0,3 {4.3.5} | Соты проточенные порядка 5 куб. |  | |
| т 0,3 {3,5,3} | Сморщенные икосаэдрические соты | 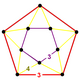 | |
| т 0,3 {5,3,5} | Ранцинированные додекаэдрические соты порядка 5 |  | |
См. также
[ редактировать ]- Однородный многогранник
- Равномерный 4-многогранник
- Ректификация (геометрия)
- Усечение (геометрия)
- Кантелляция (геометрия)
Ссылки
[ редактировать ]- Коксетер, Правильные многогранники HSM (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8 (стр. 145–154, глава 8: Усечение, стр. 210, расширение)
- Нормана Джонсона Равномерные многогранники , Рукопись (1991)
- Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.
- Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус , Симметрии вещей 2008, ISBN 978-1-56881-220-5 (глава 26)