Кантеллированный, 120 ячеек

Четыре кантелляции
Ортогональные проекции в _{H 3} плоскости Кокстера
120-ячеечный	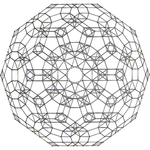Кантеллированный, 120 ячеек	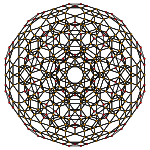Сочлененный 600-ячеечный
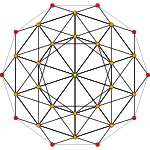600-ячеечный	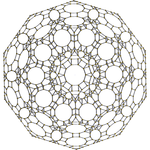Кантитусеченный, 120 ячеек	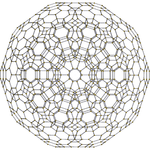Усеченный, 600 ячеек

В четырехмерной геометрии согнутый 120-ячеечный выпуклый однородный 4-мерный многогранник является кантелляцией (усечением 2-го порядка) обычного 120-ячеечного .

Существует четыре степени кантелляции 120-клеточного числа, в том числе с перестановочными усечениями. Два из них выражены относительно двойного 600-ячеечного.

Кантеллированный, 120 ячеек

Кантеллированный, 120 ячеек
Тип	Равномерный 4-многогранник
Единый индекс	37
Диаграмма Кокстера
Клетки	Всего за 1920 год: 120 (3.4.5.4) 1200 (3.4.4) 600 (3.3.3.3)
Лица	4800{3}+3600{4}+720{5}
Края	10800
Вершины	3600
Вершинная фигура	клин
Символ Шлефли	т _0,2 {5,3,3}
Группа симметрии	H ₄ , [3,3,5], порядка 14400
Характеристики	выпуклый

многогранник Сочлененный 120-клеточный представляет собой однородный 4-мерный многогранник . По своей конструкции он назван операцией Cantellation, применяемой к обычному 120-ячеечному элементу . Он содержит 1920 ячеек , в том числе 120 ромбокододекаэдров , 1200 треугольных призм , 600 октаэдров . Его вершинная фигура представляет собой клин с двумя ромбикосидодекаэдрами, двумя треугольными призмами и одним октаэдром, встречающимися в каждой вершине.

Альтернативные названия

Свернутый 120-клеточный Норман Джонсон
Кантелляционный гекатоникосахорон / Кантелляционный додекаконтахорон / Кантелляционный полидодекаэдр
Маленький ромбовидный гекатоникосахорон (аббревиатура срахи) ( Джордж Ольшевский и Джонатан Бауэрс) ^[1]
Полидодекаэдр Амбо-02 ( Джон Конвей )

Изображения

Ортографические проекции плоскостей Кокстера
H_H3	А ₂ / Б ₃ / Д ₄	А3 / _Б2
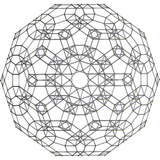[10]	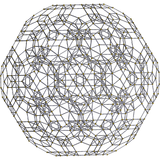[6]	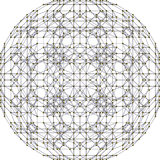[4]

Диаграмма Шлегеля . Пятиугольная грань удалена.

Кантитусеченный, 120 ячеек

Кантитусеченный, 120 ячеек
Тип	Равномерный 4-многогранник
Единый индекс	42
Символ Шлефли	т _0,1,2 {5,3,3}
Диаграмма Кокстера
Клетки	Всего за 1920 год: 120 (4.6.10) 1200 (3.4.4) 600 (3.6.6)
Лица	9120: 2400{3}+3600{4}+ 2400{6}+720{10}
Края	14400
Вершины	7200
Вершинная фигура	клиновидная кость
Группа симметрии	H ₄ , [3,3,5], порядка 14400
Характеристики	выпуклый

Кантиусеченный представляет 120-клеточный элемент собой однородный полихорон .

Этот 4-многогранник родственен обычному 120-клеточному . Операция кантитруции создает новые усеченные тетраэдрические ячейки в вершинах и треугольные призмы по краям. Исходные ячейки додекаэдра кантиусечены в большие клетки ромбикосододекаэдра.

На изображении показан 4-мерный многогранник, нарисованный в виде диаграммы Шлегеля , которая проецирует 4-мерную фигуру в 3-мерное пространство, искажая размеры ячеек. Кроме того, десятиугольные грани скрыты, что позволяет нам видеть элементы, проецируемые внутри.

Альтернативные названия

Усеченный 120-клеточный Норман Джонсон
Кантиусеченный гекатоникосахорон / Кантиусеченный полидодекаэдр
Большой ромбовидный гекатоникосахорон (аббревиатура grahi) ( Джордж Ольшевский и Джонтан Бауэрс) ^[2]
Полидодекаэдр Амбо-012 ( Джон Конвей )

Изображения

Ортографические проекции плоскостей Кокстера
H_H3	А ₂ / Б ₃ / Д ₄	А3 / _Б2
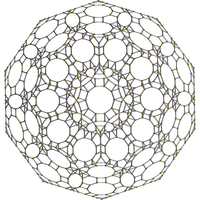[10]	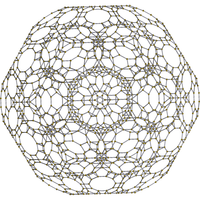[6]	[4]

Диаграмма Шлегеля
В центре усеченная ячейка икосододекаэдра со скрытыми десятиугольными гранями.

Сочлененный 600-ячеечный

Сочлененный 600-ячеечный
Тип	Равномерный 4-многогранник
Единый индекс	40
Символ Шлефли	т _0,2 {3.3.5}
Диаграмма Кокстера
Клетки	1440 всего: 120 3.5.3.5 600 3.4.3.4 720 4.4.5
Лица	8640 всего: (1200+2400){3} +3600{4}+1440{5}
Края	10800
Вершины	3600
Вершинная фигура	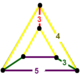равнобедренная треугольная призма
Группа симметрии	H ₄ , [3,3,5], порядка 14400
Характеристики	выпуклый

многогранник Сочлененный 600-клеточный представляет собой однородный 4-мерный многогранник . Он имеет 1440 ячеек: 120 икосододекаэдров , 600 кубооктаэдров и 720 пятиугольных призм . Его вершинная фигура представляет собой равнобедренную треугольную призму , определяемую одним икосододекаэдром, двумя кубооктаэдрами и двумя пятиугольными призмами.

Альтернативные названия

Свернутый 600-клеточный Норман Джонсон
Кантелляционный гексакосихорон / Кантелляционный тетраплекс
Маленький ромбигексакосихорон (аббревиатура srix) ( Джордж Ольшевский и Джонатан Бауэрс) ^[3]
Тетраплекс Амбо-02 ( Джон Конвей )

Строительство

Этот 4-многогранник имеет ячейки в 3 из 4 позиций фундаментальной области, извлеченной из диаграммы Кокстера путем удаления одного узла за раз:

Узел	Заказ	Клетка
0	600	Скошенный тетраэдр ( Кубооктаэдр )
1	1200	Никто (Вырожденная треугольная призма)
2	720	Пятиугольная призма
3	120	Выпрямленный додекаэдр ( Икосододекаэдр )

находится 1440 пятиугольных граней Между икосододекаэдрами и пятиугольными призмами . находится 3600 квадратов Между кубооктаэдрами и пятиугольными призмами . Между икосододекаэдрами и кубооктаэдрами имеется 2400 треугольных граней, а между парами кубооктаэдров — 1200 треугольных граней.

Существует два класса ребер: 3-4-4, 3-4-5: 3600 имеет два квадрата и треугольник вокруг него, а 7200 — один треугольник, один квадрат и один пятиугольник.

Изображения

Ортографические проекции плоскостей Кокстера
Ч ₄	-
[30]	[20]
F_F4	H_H3
[12]	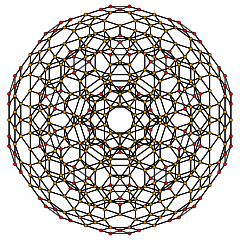[10]
А ₂ / Б ₃ / Д ₄	А3 / _Б2
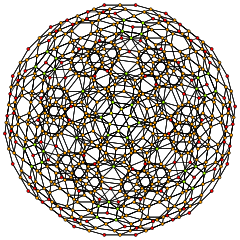[6]	[4]

Диаграммы Шлегеля
	Стереографическая проекция с 3600 зелеными треугольными гранями и 3600 синими квадратными гранями.

Усеченный, 600 ячеек

Усеченный, 600 ячеек
Тип	Равномерный 4-многогранник
Единый индекс	45
Диаграмма Кокстера
Клетки	1440 всего: 120 (5.6.6) 720 (4.4.5) 600 (4.6.6)
Лица	8640: 3600{4}+1440{5}+ 3600{6}
Края	14400
Вершины	7200
Вершинная фигура	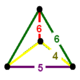клиновидная кость
Символ Шлефли	т _0,1,2 {3,3,5}
Группа симметрии	H ₄ , [3,3,5], порядка 14400
Характеристики	выпуклый

Кантиусеченный 600-ячеечный представляет собой однородный 4-многогранник . Он состоит из 1440 ячеек : 120 усеченных икосаэдров , 720 пятиугольных призм и 600 усеченных октаэдров . Он имеет 7200 вершин, 14400 ребер и 8640 граней (3600 квадратов, 1440 пятиугольников и 3600 шестиугольников). Он имеет неправильную вершинную тетраэдрическую фигуру , заполненную одним усеченным икосаэдром, одной пятиугольной призмой и двумя усеченными октаэдрами.

Альтернативные названия

Усеченный 600-ячеечный ( Норман Джонсон )
Кантиусеченный гексакосихорон / Кантиусеченный полидодекаэдр
Большой ромбовидный гексакосихорон (аббревиатура grix ) ( Джордж Ольшевский и Джонатан Бауэрс) ^[4]
Политетраэдр Амбо-012 ( Джон Конвей )

Изображения

Диаграмма Шлегеля

Ортографические проекции плоскостей Кокстера
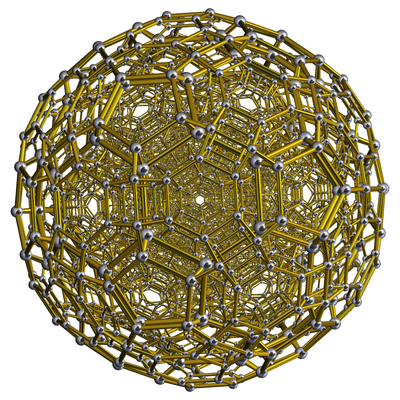H_H3	А ₂ / Б ₃ / Д ₄	А3 / _Б2
[10]	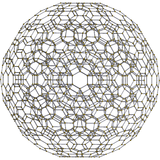[6]	[4]

Связанные многогранники

H ₄Многогранники семейства
120-cell	rectified 120-cell	truncated 120-cell	cantellated 120-cell	runcinated 120-cell	cantitruncated 120-cell	runcitruncated 120-cell	omnitruncated 120-cell

{5,3,3}	r{5,3,3}	t{5,3,3}	rr{5,3,3}	t_0,3{5,3,3}	tr{5,3,3}	t_0,1,3{5,3,3}	t_0,1,2,3{5,3,3}


600-cell	rectified 600-cell	truncated 600-cell	cantellated 600-cell	bitruncated 600-cell	cantitruncated 600-cell	runcitruncated 600-cell	omnitruncated 600-cell

{3,3,5}	r{3,3,5}	t{3,3,5}	rr{3,3,5}	2t{3,3,5}	tr{3,3,5}	t_0,1,3{3,3,5}	t_0,1,2,3{3,3,5}

Примечания

^ Клитцинг, (o3x3o5x - срахи)
^ Клитцинг, (o3x3x5x - грахи)
^ Клитцинг, (x3o3x5o - шрикс)
^ Клитцинг, (x3x3x5o - грикс)

Ссылки

Выпуклая равномерная полихора на основе гекатоникосахорона (120-клеточного) и гексакосихорона (600-клеточного) — Модель 37 , Георгий Ольшевский.
Архимедский Полихор Nr. 57 (сочлененные 120-ячеечные) архимедовы многогранники Марко Мёллера в R ⁴ (Немецкий)
Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380-407, МР 2,10]
- (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
- (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
Дж. Х. Конвей и М. Дж. Т. Гай : Четырехмерные архимедовы многогранники , материалы коллоквиума по выпуклости в Копенгагене, стр. 38 и 39, 1965 г.
Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.
Четырехмерные архимедовы многогранники (немецкий), Марко Мёллер, докторская диссертация, 2004 г. [1]. Архивировано 22 марта 2005 г. в Wayback Machine m63 m61 m56.
Выпуклая равномерная полихора на основе гекатоникосахорона (120-клеточного) и гексакосихорона (600-клеточного) — Модель 40, 42, 45 , Георгий Ольшевский.
Клитцинг, Ричард. «4D однородные многогранники (полихора)» . о3х3о5х - срахи, о3х3х5х - грахи, х3о3х5о - шрикс, х3х3х5о - грикс

Внешние ссылки

Четырехмерная проекция многогранника Barn Raisings ( конструкция Zometool из скошенных 120 ячеек ), Джордж У. Харт
Проект Zome Renaissance Banff 2005 : модель Zome трехмерной ортогональной проекции сочлененных 600 ячеек.
Однородные многогранники H4 с координатами: rr{3,3,5} rr{5,3,3} tr{3,3,5} tr{5,3,3}

v т и Фундаментальные выпуклые правильные и однородные многогранники размерностей 2–10.
Семья	н	Б _н	И ₂ (п) / Д _н	Е ₆ / Е ₇ / Е ₈ / Ж ₄ / Г ₂	Ч _н
Правильный многоугольник	Треугольник	Квадрат	п-гон	Шестиугольник	Пентагон
Однородный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный полихорон	Пентахорон	16 ячеек • Тессеракт	Демитессеракт	24-ячеечный	120 ячеек • 600 ячеек
Равномерный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-демикуб
Равномерный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-демикуб	1 ₂₂ • 2 ₂₁
Равномерный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-демикуб	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Равномерный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-демикуб	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Равномерный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-демикуб
Равномерный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-демикуб
Равномерный n - многогранник	n - симплекс	n - ортоплекс • n - куб	n - демикуб	1 _{лиц 2} • 2 _{лиц 1} • лиц ₂₁	n - пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений.

[1] Клитцинг, (o3x3o5x - срахи)

[2] Клитцинг, (o3x3x5x - грахи)

[3] Клитцинг, (x3o3x5o - шрикс)

[4] Клитцинг, (x3x3x5o - грикс)

[1]

[2]

[3]

[4]