Ромбикосидодекаэдр
| Ромбикосидодекаэдр | |
|---|---|
 (Нажмите здесь, чтобы увидеть вращающуюся модель) | |
| Тип | Архимедово тело Однородный многогранник |
| Элементы | F = 62, E = 120, V = 60 (χ = 2) |
| Лица по сторонам | 20{3}+30{4}+12{5} |
| Обозначение Конвея | ЭД или ААД |
| Символы Шлефли | рр{5,3} или |
| т 0,2 {5,3} | |
| Символ Витхоффа | 3 5 | 2 |
| Диаграмма Кокстера | |
| Группа симметрии | I h , H 3 , [5,3], (*532), порядок 120 |
| Группа вращения | Я , [5,3] + , (532), порядок 60 |
| Двугранный угол | 3-4: 159°05′41″ (159.09°) 4-5: 148°16′57″ (148.28°) |
| Ссылки | Ю 27 , Ц 30 , Ж 14 |
| Характеристики | Полуправильный выпуклый |
 Цветные лица |  3.4.5.4 ( фигура вершины ) |
 Дельтоидный шестиконтаэдр ( двойной многогранник ) |  Сеть |
В геометрии ромбокосододекаэдр непризматических тел , — архимедово тело , одно из тринадцати выпуклых изогональных состоящих из двух или более типов правильных многоугольных граней .
Он имеет 20 правильных треугольных граней, 30 квадратных граней, 12 правильных пятиугольных граней, 60 вершин и 120 ребер .
Имена
[ редактировать ]Иоганн Кеплер в «Harmonices Mundi» (1618) назвал этот многогранник ромбикосододекаэдром , что является сокращением от усеченного икосододекаэдра ромба , причем икосододекаэдрический ромб был его именем для ромбического триаконтаэдра . [1] [2] Существуют различные варианты усечения ромбического триаконтаэдра в топологический ромбикосододекаэдр: в первую очередь его выпрямление (слева), то, которое создает однородное твердое тело (в центре), и выпрямление двойственного икосододекаэдра (справа), которое является ядром двойного соединения. .
Размеры
[ редактировать ]Для ромбокосододекаэдра с длиной ребра a его площадь поверхности и объем равны:
Геометрические отношения
[ редактировать ]Если вы расширите икосододекаэдр , отодвинув грани от начала координат на нужное расстояние, не меняя ориентацию или размер граней, и заделаете в результате квадратные отверстия, вы получите ромбокосододекаэдр. Следовательно, он имеет такое же количество треугольников, как икосаэдр, и такое же количество пятиугольников, как и додекаэдр, с квадратом на каждом ребре.
Альтернативно, если вы расширите каждый из пяти кубов, отодвинув грани от начала координат на нужную величину и повернув каждый из пяти на 72° вокруг так, чтобы они были на одинаковом расстоянии друг от друга, без изменения ориентации или размера граней, и исправьте пятиугольные и треугольные отверстия, в результате получится ромбокосододекаэдр. Следовательно, в нем столько же квадратов, сколько в пяти кубах.
Две группы граней билунабиротонды , лун ( каждая луна представляет собой два треугольника, примыкающих к противоположным сторонам одного квадрата), могут быть выровнены с конгруэнтным участком граней на ромбокосододекаэдре. Если таким образом выровнять две билунабиротонды на противоположных сторонах ромбокосододекаэдра, то между билунабиротондами в самом центре ромбикосододекаэдра можно поставить куб.
Ромбикосидодекаэдр разделяет расположение вершин с маленьким звездчатым усеченным додекаэдром и с однородными соединениями шести или двенадцати пентаграммных призм .
В наборах Zometool для изготовления геодезических куполов и других многогранников в качестве соединителей используются шарики с прорезями. Шары представляют собой «расширенные» ромбокододекаэдры, в которых квадраты заменены прямоугольниками. Расширение выбирается таким образом, чтобы полученные прямоугольники были золотыми прямоугольниками .
Двенадцать из 92 тел Джонсона произошли от ромбикосододекаэдра, четыре из них - в результате вращения одного или нескольких пятиугольных куполов : вращающийся , парабигиратный , метабигиратный и тригиратный ромбикосидодекаэдр . Еще восемь можно построить, удалив до трех куполов, а иногда также повернув один или несколько других куполов.
Декартовы координаты
[ редактировать ]Декартовы координаты вершин ромбокосододекаэдра с длиной ребра 2 и центром в начале координат являются четными перестановками : [3]
- (±1, ±1, ± φ 3 ),
- (± φ 2 , ± φ , ±2 φ ),
- (±(2+ φ ), 0, ± φ 2 ),
где φ = 1 √ 5/2 + — золотое сечение . Следовательно, радиус описанной окружности этого ромбокосододекаэдра равен общему расстоянию этих точек от начала координат, а именно √ φ 6 +2 = √ 8φ+7 для длины ребра 2. Для единичной длины ребра R необходимо уменьшить вдвое, что дает
- Р = √ 8 φ +7 / 2 = √ 11+4 √ 5 / 2 ≈ 2.233.
Ортогональные проекции
[ редактировать ]Ромбикосидодекаэдр . имеет шесть особых ортогональных проекций , центрированных на вершине, на двух типах ребер и трех типах граней: треугольниках, квадратах и пятиугольниках Последние два соответствуют A 2 и H 2 плоскостям Кокстера .
| В центре | Вертекс | Край 3-4 | Край 5-4 | Лицо Квадрат | Лицо Треугольник | Лицо Пентагон |
|---|---|---|---|---|---|---|
| Твердый |  |  |  | |||
| Каркас |  |  |  |  |  |  |
| Проективный симметрия | [2] | [2] | [2] | [2] | [6] | [10] |
| Двойной изображение |  |  |  |  |  |  |
Сферическая черепица
[ редактировать ]Ромбикосидодекаэдр также можно представить в виде сферической мозаики и спроецировать на плоскость с помощью стереографической проекции . Эта проекция является равноугольной , сохраняя углы, но не площади или длины. Прямые линии на сфере проецируются на плоскость в виде дуг окружностей.
 |  Пятиугольник в центре |  Треугольник -центрированный |  Квадрат -центрированный |
| Ортографическая проекция | Стереографические проекции | ||
|---|---|---|---|
Связанные многогранники
[ редактировать ]

| Семейство однородных икосаэдрических многогранников. |
|---|
Мутации симметрии
[ редактировать ]Этот многогранник топологически связан как часть последовательности согнутых многогранников с фигурой вершины (3.4.n.4), которая продолжается как мозаика гиперболической плоскости . Эти вершинно-транзитивные фигуры обладают (*n32) отражательной симметрией .
| * n 32 мутация симметрии развернутых мозаик: 3.4. № .4 |
|---|
Твердые вещества Джонсона
[ редактировать ]Существует 12 родственных тел Джонсона , 5 по уменьшению и 8, включая вращения:
J5  | 76  | 80  | 81  | 83  |
72  | 73  | 74  | 75  |
77  | 78  | 79  | 82  |
Расположение вершин
[ редактировать ]ромбикосододекаэдра разделяет Расположение вершин три невыпуклых однородных многогранника : маленький звездчатый усеченный додекаэдр , малый додецикосододекаэдр (имеющий общие треугольные и пятиугольные грани) и малый ромбидодекаэдр (имеющий общие квадратные грани).
Расположение вершин у него также такое же, как у соединений шести однородных или двенадцати пентаграммных призм .
 Ромбикосидодекаэдр |  Малый додецикосододекаэдр |  Малый ромбидодекаэдр |
 Малый звездчатый усеченный додекаэдр |  Соединение шести пентаграммных призм. |  Соединение двенадцати пентаграммных призм. |
Ромбикосидодекаэдрический граф
[ редактировать ]| Ромбикосидодекаэдрический граф | |
|---|---|
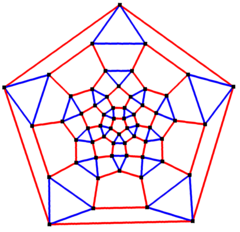 Диаграмма Шлегеля с центром в Пентагоне | |
| Вершины | 60 |
| Края | 120 |
| Автоморфизмы | 120 |
| Характеристики | Граф четвертой степени , гамильтониан , регулярный |
| Таблица графиков и параметров | |
В математической области теории графов ромбокосододекаэдрический граф — это график вершин и ребер ромбокосододекаэдра, одного из архимедовых тел . Он имеет 60 вершин и 120 ребер и является четвертой степени архимедовым графом . [5]

См. также
[ редактировать ]Примечания
[ редактировать ]- ^ Джона Кеплера [ т.е. ] Иоганна Кеплера (1619). «Книга II. О сравнении гармонических фигур. 28. Предложение». [Книга II. О равенстве гармонических фигур. Предложение 28.]. Harmonices Mundi Libri V [ Гармония мира в пяти книгах ]. Линц, Австрия: Sumptibus Godofredi Tampachii bibl. Франко напечатано Джоном Планком [опубликовано Готфридом Тамбахом [...] напечатано Иоганном Планком]. п. 64. OCLC 863358134 .
Поэтому один тригон с двумя тетрагонами и с одним пятиугольником составляют менее 4 прямых линий и согласовывают 20 тригонов с 30 тетрагонами и 12 пятиугольниками в один шестигранник, который я называю ромбикосидодекаэдром, ſeu ectum Rhombus Icoſidododecaedricum.
- ^ Гармонии мира Иоганна Кеплера, переведено на английский язык с введением и примечаниями Э. Дж. Эйтона , А. М. Дункана , Дж. В. Филда , 1997, ISBN 0-87169-209-0 (стр. 123)
- ^ Вайсштейн, Эрик В. «Группа икосаэдра» . Математический мир .
- ^ Вайсштейн, Эрик В. «Зоме» . Математический мир .
- ^ Читай, RC; Уилсон, Р.Дж. (1998), Атлас графиков , Oxford University Press , стр. 269
Ссылки
[ редактировать ]- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. ISBN 0-486-23729-Х . (Раздел 3-9)
- Кромвель, П. (1997). Многогранники . Великобритания: Кембридж. С. 79–86 Архимедовы тела . ISBN 0-521-55432-2 .
- Теория большого взрыва, серия 8, серия 2 — Решение младшего профессора : представляет собой ответ на импровизированную научную викторину, которую четыре главных героя проводят в квартире Леонарда и Шелдона, а также проиллюстрировано в « Тщеславной карточке» Чака Лорри № 461 на сайте конец этого эпизода.
Внешние ссылки
[ редактировать ]- Вайсштейн, Эрик В. , « Маленький ромбикосододекаэдр » (« Архимедово тело ») в MathWorld .
- Клитцинг, Ричард. «3D выпуклые однородные многогранники x3o5x — срид» .
- Редактируемая для печати сетка ромбикосододекаэдра с интерактивным 3D-просмотром
- Однородные многогранники
- Многогранники виртуальной реальности Энциклопедия многогранников











































