Строительство Витхоффа

В геометрии конструкция Витгофа , названная в честь математика Виллема Абрахама Витгофа , представляет собой метод построения однородного многогранника или плоской мозаики . Ее часто называют калейдоскопической конструкцией Витхоффа.

Процесс строительства

Метод основан на идее замощения сферы . сферическими треугольниками – см. Шварца Треугольники Эта конструкция располагает три зеркала по сторонам треугольника, как в калейдоскопе . Однако, в отличие от калейдоскопа, зеркала не параллельны, а пересекаются в одной точке. Таким образом, они заключают сферический треугольник на поверхности любой сферы с центром в этой точке, и повторяющиеся отражения создают множество копий треугольника. Если углы сферического треугольника выбраны правильно, треугольники покроют сферу плиткой один или несколько раз.

Если поместить вершину в подходящую точку внутри сферического треугольника, окруженного зеркалами, можно добиться того, что отражения от этой точки образуют однородный многогранник. Для сферического треугольника ABC у нас есть четыре возможности создать однородный многогранник:

Вершина помещена в А. точку В результате получается многогранник с символом Витхоффа a | b c , где a равно π, разделенному на угол треугольника в точке A , и аналогично для b и c .
Вершина расположена в точке на прямой AB так, что она делит угол C пополам . В результате получается многогранник с символом Витхоффа a b | в .
Вершина размещается так, чтобы она находилась центре ABC в . В результате получается многогранник с символом Витхоффа a b c |.
Вершина находится в такой точке, что при повороте ее вокруг любого из углов треугольника на двойной угол в этой точке она смещается на одинаковое расстояние для каждого угла. Используются только четные отражения исходной вершины. Многогранник имеет символ Витгофа | а б в .

более высокой размерности Этот процесс в целом также применим для правильных многогранников , включая 4-мерные однородные 4-многогранники .

Примеры
Шестиугольная призма состоит из семейств (6 2 2) и (3 2 2).	Усеченная квадратная мозаика построена по двум различным позициям симметрии в семействе (4 4 2).	Шаблон Витхоффа pq2 \| = 432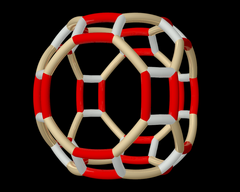\|. Орбита узора Витгофа выше под действием полной октаэдрической группы .

Невитоффовы конструкции

Однородные многогранники , которые не могут быть созданы с помощью зеркальной конструкции Витгофа, называются невитоффовыми. Обычно их можно получить из форм Витоффа либо путем чередования (удаления альтернативных вершин), либо путем вставки чередующихся слоев частичных фигур. Оба этих типа фигур будут содержать вращательную симметрию. Иногда курносые формы считают витоффовскими, хотя они могут быть построены только путем чередования всеусеченных форм.

Примеры
Шестиугольная антипризма построена чередованием двенадцатиугольной призмы .	Удлиненная треугольная плитка состоит из наслоения квадратных плиток и рядов треугольных плиток .	Большой диромбикосидодекаэдр — единственный невитоффов однородный многогранник.

См. также

Символ Витгофа — обозначение конструкции Витгофа из однородных многогранников и однородных мозаик .
Диаграмма Кокстера – Дынкина - обобщенный символ конструкции Витгофа однородных многогранников и сот.

Ссылки

Кокстера Регулярные многогранники , третье издание, (1973), Дуврское издание, ISBN 0-486-61480-8 (Глава V: Калейдоскоп, раздел: 5.7 Конструкция Витхоффа)
Коксетер Красота геометрии: двенадцать эссе , Dover Publications, 1999, ISBN 0-486-40919-8 (Глава 3: Конструкция Витгофа для однородных многогранников)
Хар'Эл, З. Единообразное решение для однородных многогранников. , Geometriae Dedicata 47, 57-110, 1993. [1] (Раздел 4: Калейдоскоп)
В. А. Витхофф , Связь между многогранниками семейства C600 , Koninklijke Akademie van Wetenschappen te Amsterdam, Proceedings of the Sciences, 20 (1918) 966–970.

Внешние ссылки

Апплет Грега Игана для отображения однородных многогранников с использованием метода построения Витхоффа.
Рендеринг метода строительства Витхоффа в Shadertoy.
Дженн , программное обеспечение, которое генерирует изображения (сферических) многогранников и многохор на основе групп симметрии.