Великий дуоантипризм

Великий дуоантипризм
Тип	Равномерный полихорон
Символы Шлефли	$с{5}с{5/3} {5}\otimes{5/3} ч{10}с{5/3} с{5}ч{10/3} ч{10}ч{10/3}$
Диаграммы Кокстера
Клетки	50 тетраэдров 10 пятиугольных антипризм 10 пентаграммных скрещенных антипризм
Лица	200 треугольников 10 пятиугольников 10 пентаграмм
Края	200
Вершины	50
Вершинная фигура	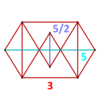звезда- гиробифастигий
Группа симметрии	$[5,2,5] +,$ заказ 50 $[(5,2) +,10],$ порядок 100 $[10,2 +,10],$ порядка 200
Характеристики	Вертекс-равномерный
Сеть (перекрывающаяся в пространстве)

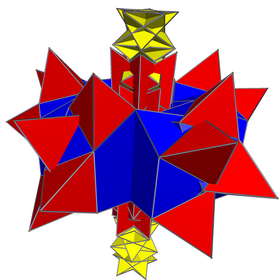
В геометрии большая дуоантипризма — единственное однородное звездной дуоантипризмы решение $p = 5,$ $q = .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ 5/3 геометрии ⁠ , мерной$ в 4- . Он имеет символ Шлефли ${5}\otimes{5/3},$ $s{5}s{5/3}$ или $ht 0,1,2,3 {5,2,5/3},$ диаграмма Кокстера. , построенный из 10 пятиугольных антипризм , 10 пентаграммных скрещенных антипризм и 50 тетраэдров .

Его вершины являются подмножеством вершин маленького звездчатого 120-ячеечного .

Строительство

Большая дуоантипризма может быть построена из неоднородного варианта дуопризмы 10-10/3 (дуопризма декагона и декаграммы ) , где длина ребра декаграммы примерно в 1,618 раз ( золотое сечение ) превышает длину ребра декагона путем чередования . процесс. Десятиугольные призмы чередуются с пятиугольными антипризмами , декаграммные призмы чередуются с пентаграммными скрещенными антипризмами с новыми правильными тетраэдрами , созданными в удаленных вершинах. Это единственное единообразное решение для дуоантипризмы pq, помимо обычной 16-ячеечной (как дуоантипризма 2-2).

Изображения

стереографическая проекция с центром в одной пентаграммной скрещенной антипризме.	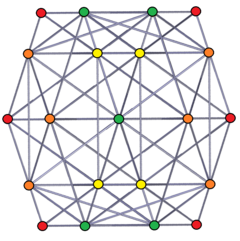Ортогональные проекции , с вершинами, окрашенными перекрытием, красным, оранжевым, желтым, зеленым имеют кратность 1, 2, 3,4.

Другие имена

Великая дуоантипризма (гудап) Джонатан Бауэрс ^[1]^[2]

Ссылки

^ Джонатан Бауэрс - Разная униформа Полихора 965. Гудап
^ http://www.polychora.com/12GudapsMovie.gif Архивировано 22 февраля 2014 г. на Wayback Machine. Анимация поперечных сечений.

Правильные многогранники , HSM Coxeter , Dover Publications, Inc., 1973, Нью-Йорк, с. 124.
Нормана Джонсона Равномерные многогранники , Рукопись (1991)
- Н. В. Джонсон : Теория однородных многогранников и сот , доктор философии. Диссертация, Университет Торонто, 1966 г.
Клитцинг, Ричард. "4D однородные многогранники (полихоры) s5/3s2s5s - гудап" .

Эта из 4-х многогранников статья незавершена . Вы можете помочь Википедии, расширив ее .

[1] Джонатан Бауэрс - Разная униформа Полихора 965. Гудап

[2] ttp://www.polychora.com/12GudapsMovie.gif Архивировано 22 февраля 2014 г. на Wayback Machine. Анимация поперечных сечений.

[1]

[2]