Петри двойной

Многоугольник Петри додекаэдра представляет собой косой десятиугольник . Если смотреть на 5-кратную ось симметрии твердого тела, оно выглядит как правильный десятиугольник. Каждая пара последовательных сторон принадлежит одному пятиугольнику (но не тройка).

В топологической теории графов вложенному двойственный Петри ( графу на 2- многообразии со всеми гранями дисков) — это другой вложенный граф, гранями которого являются многоугольники Петри первого вложения. ^[1]

Двойственный Петри также называется Петриалом и двойственным Петри встроенного графа. $G$ может быть обозначен $G^{\pi }$ . ^[2]Его можно получить из знаковой системы вращения или представления вложения в виде ленточного графа путем скручивания каждого ребра вложения.

Характеристики

Как и в случае с обычным двойственным графом , повторение двойственной операции Петри дважды возвращает к исходному вложению поверхности.В отличие от обычного двойственного графа (который представляет собой вложение вообще другого графа в одну и ту же поверхность), двойственный граф Петри представляет собой вложение того же графа в вообще другую поверхность. ^[1]

Поверхностная двойственность и двойственность Петри — две из шести операций Вильсона , которые вместе образуют группу этих операций. ^[3]

Правильные многогранники

Применение двойственного Петри к правильному многограннику дает правильное отображение . ^[2] Число косых h -угольных граней равно g /2 h , где g — порядок группы , а h — номер Кокстера группы.

Например, двойственный кубу Петри ( двудольный граф с восемью вершинами и двенадцатью ребрами, вложенный в сферу с шестью квадратными гранями)имеет четыре ^[4] шестиугольные грани, экваторы куба. Топологически он образует вложение того же графа в тор. ^[1]

Таким образом получаются следующие регулярные отображения.

Петриальный тетраэдр , {3,3} ^$п$, имеет 4 вершины, 6 ребер и 3 скошенные квадратные грани. С эйлеровой характеристикой , χ равной 1, он топологически идентичен полукубу { 4,3}/2.
Петриальный куб , {4,3} ^$п$, имеет 8 вершин, 12 ребер и 4 косых шестиугольника, окрашенных в красный, зеленый, синий и оранжевый цвета. Поскольку эйлерова характеристика равна 0, ее также можно увидеть на четырех шестиугольных гранях шестиугольной мозаики как тип {6,3} _(2,0) .
Петриальный октаэдр , {3,4} ^$п$, имеет 6 вершин, 12 ребер и 4 косых грани шестиугольника. Он имеет эйлерову характеристику −2 и имеет отображение в гиперболическую шестиугольную мозаику порядка 4 как тип {6,4} ₃ .
Петриальный додекаэдр , {5,3} ^$п$, имеет 20 вершин, 30 ребер и 6 косых десятиугольных граней, а также эйлерову характеристику −4, связанную с гиперболическим мозаикой типа {10,3} ₅ .
Петриальный икосаэдр , {3,5} ^$п$, имеет 12 вершин, 30 ребер и 6 косых десятиугольных граней, а также эйлерову характеристику −12, связанную с гиперболическим мозаикой типа {10,5} ₃ .

Регулярные петриалы
Имя	каменный тетраэдр	каменный куб	каменный октаэдр	каменный додекаэдр	каменный икосаэдр
Символ	{3,3} ^$п$ , {4,3} ₃	{4,3} ^$п$ , {6,3} ₄	{3,4} ^$п$ , {6,4} ₃	{5,3} ^$п$ , {10,3}	{3,5} ^$п$ , {10,5}
(v,e,f), χ	(4,6,3), х = 1	(8,12,4), х = 0	(6,12,4), χ = −2	(20,30,6), χ = −4	(12,30,6), χ = −12
Лица	3 перекошенных квадрата	4 косых шестиугольника		6 косых десятиугольников
Лица	3 перекошенных квадрата
Изображение
Анимация
Связанный цифры	{4,3} ₃ = {4,3}/2 = {4,3} _(2,0)	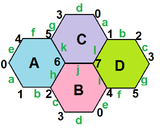{6,3} ₃ = {6,3} _(2,0)	{6,4} ₃ = {6,4} _(4,0)	{10,3} ₅	{10,5} ₃

Есть также 4 петриала многогранников Кеплера – Пуансо :

Петриальный большой додекаэдр , {5,5/2} ^$п$, имеет 12 вершин, 30 ребер и 10 косых граней шестиугольника с эйлеровой характеристикой , χ равной -8.
Петриальный малый звездчатый додекаэдр , {5/2,5} ^$п$, имеет 12 вершин, 30 ребер и 10 косых граней шестиугольника с χ, равным -8.
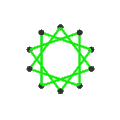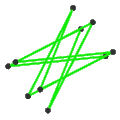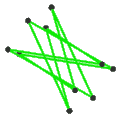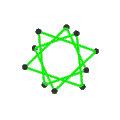
Петриальный большой икосаэдр , {3,5/2} ^$п$, имеет 12 вершин, 30 ребер и 6 косых декаграммных граней с χ, равным -12.
Петриальный большой звездчатый додекаэдр , {5/2,3} ^$п$, имеет 20 вершин, 30 ребер и 6 косых декаграммных граней с χ, равным -4.

Обычные звездные петриалы
Имя	каменный большой додекаэдр	каменный маленький звездчатый додекаэдр	каменный большой икосаэдр	каменный отличный звездчатый додекаэдр
Символ	{5,5/2} ^$п$ , {6,5/2}	{5/2,5} ^$п$ , {6,5}	{3,5/2} ^$п$ , {10/3,5/2}	{5/2,3} ^$п$ , {10/3,3}
(v,e,f), χ	(12,30,10), х = -8	(12,30,10), х = -8	(12,30,6), х = -12	(20,30,6), х = -4
Лица	10 косых шестиугольников		6 перекошенных декаграмм (одна декаграмма синего цвета обведена контуром)
Лица
Изображение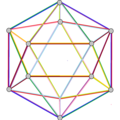
Анимация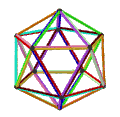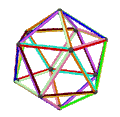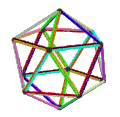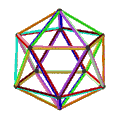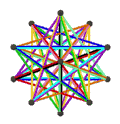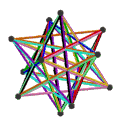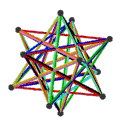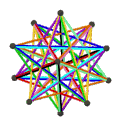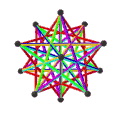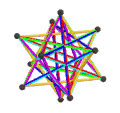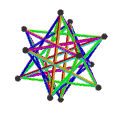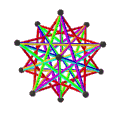

Ссылки

^ Jump up to: Перейти обратно: ^а ^б ^с Писански, Томаж ; Рандич, Милан (2000), «Мосты между геометрией и теорией графов», в Горини, Кэтрин А. (редактор), Геометрия в действии , Примечания MAA, том. 53, Вашингтон, округ Колумбия: Матем. доц. Америка, стр. 174–194, MR 1782654 . См., в частности, стр. 181 .
^ Jump up to: Перейти обратно: ^а ^б Макмаллен, Питер; Шульте, Эгон (2002), Абстрактные правильные многогранники , Энциклопедия математики и ее приложений, том. 92, Издательство Кембриджского университета, с. 192, ИСБН 9780521814966
^ Джонс, Джорджия; Торнтон, Дж. С. (1983), «Операции над отображениями и внешние автоморфизмы», Журнал комбинаторной теории , серия B, 35 (2): 93–103, doi : 10.1016/0095-8956(83)90065-5 , MR 0733017
^ Октаэдрическая симметрия - порядок 48, число Кокстера - 6, 48/(2×6)=4.

[pr-1] Jump up to: Перейти обратно: ^а ^б ^с Писански, Томаж ; Рандич, Милан (2000), «Мосты между геометрией и теорией графов», в Горини, Кэтрин А. (редактор), Геометрия в действии , Примечания MAA, том. 53, Вашингтон, округ Колумбия: Матем. доц. Америка, стр. 174–194, MR 1782654 . См., в частности, стр. 181 .

[arp-2] Jump up to: Перейти обратно: ^а ^б Макмаллен, Питер; Шульте, Эгон (2002), Абстрактные правильные многогранники , Энциклопедия математики и ее приложений, том. 92, Издательство Кембриджского университета, с. 192, ИСБН 9780521814966

[jt-3] Джонс, Джорджия; Торнтон, Дж. С. (1983), «Операции над отображениями и внешние автоморфизмы», Журнал комбинаторной теории , серия B, 35 (2): 93–103, doi : 10.1016/0095-8956(83)90065-5 , MR 0733017

[4] Октаэдрическая симметрия - порядок 48, число Кокстера - 6, 48/(2×6)=4.

[1]

[2]

[3]

[4]