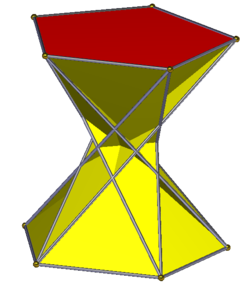
Пятиугольная антипризма

Равномерная пятиугольная антипризма
Тип	Призматический однородный многогранник
Элементы	Ф = 12, Е = 20 V = 10 (χ = 2)
Лица по сторонам	10{3}+2{5}
Символ Шлефли	с{2,10} ср{2,5}
Символ Витхоффа	| 2 2 5
Диаграмма Кокстера
Группа симметрии	Д 5д , [2 + ,10], (2*5), порядок 20
Группа вращения	Д 5 , [5,2] + , (522), порядок 10
Ссылки	У 77(с)
Двойной	Пятиугольный трапецоэдр
Характеристики	выпуклый
Вершинная фигура 3.3.3.5

Трехмерная модель (однородной) пятиугольной антипризмы

В геометрии пятиугольная антипризма — третья в бесконечном множестве антипризм, образованных четной последовательностью сторон треугольника, закрытых двумя вершинами многоугольников. Он состоит из двух пятиугольников, соединенных друг с другом кольцом из десяти треугольников , всего двенадцать граней. Следовательно, это неправильный додекаэдр .

Геометрия

Если все грани пятиугольной антипризмы правильные, то это полуправильный многогранник . Его также можно рассматривать как парабиди-уменьшенный икосаэдр , форму, образованную удалением двух пятиугольных пирамид из правильного икосаэдра, оставляя две несмежные пятиугольные грани; родственная форма, метабидиминированный икосаэдр (одно из тел Джонсона ), также образуется из икосаэдра путем удаления двух пирамид, но его пятиугольные грани примыкают друг к другу. Две пятиугольные грани любой формы можно дополнить пирамидами, чтобы сформировать икосаэдр.

Отношение к многогранникам

Пятиугольная антипризма встречается как составной элемент в некоторых многогранниках более высокой размерности . Два кольца из десяти пятиугольных антипризм каждое ограничивали гиперповерхность четырехмерной большой антипризмы . Если эти антипризмы дополнить пятиугольными призматическими пирамидами и соединить кольцами по пять тетраэдров в каждом, 600-ячеечная структура получится .

См. также

Пятиугольную антипризму можно усечь и чередовать, чтобы сформировать курносую антипризму :

Курносые антипризмы

Антипризма А5	Усечено та5	Чередование htA5
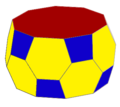с{2,10}	ц{2,10}	сс{2,10}
в:10; е:20; ф:12	в:40; е:60; ф:22	в:20; е:50; ф:32

Семейство однородных n -угольных антипризм скрывать

Название антипризмы	Дигональная антипризма	(Треугольный) Треугольная антипризма	(Тетрагональный) Квадратная антипризма	Пятиугольная антипризма	Шестиугольная антипризма	Семиугольная антипризма	...	Апейрогональная антипризма
Изображение многогранника							...
Сферическое мозаичное изображение							Плоское мозаичное изображение
Конфигурация вершины.	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	...	∞.3.3.3

Скрещенная антипризма

Перекрещенная пятиугольная антипризма топологически идентична пятиугольной антипризме , хотя ее нельзя сделать однородной. Стороны представляют собой равнобедренные треугольники . Он имеет _{d 5d} симметрию , порядок 10. Его конфигурация вершин 3,3/2,3,5, с одним ретроградным треугольником, а расположение вершин такое же, как у пятиугольной призмы .

Внешние ссылки

• Вайсштейн, Эрик В. «Антипризма» . Математический мир .
• [1]
• Пятиугольная антипризма: интерактивная модель многогранника
• Многогранники виртуальной реальности www.georgehart.com: Энциклопедия многогранников
  • VRML Модель
• многогранник А5