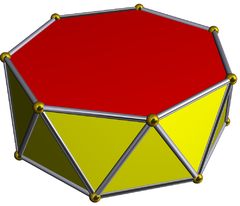
Семиугольная антипризма

Однородная семиугольная антипризма
Тип	Призматический однородный многогранник
Элементы	Ф = 16, Е = 28 V = 14 (χ = 2)
Лица по сторонам	14{3}+2{7}
Символ Шлефли	с{2,14} ср{2,7}
Символ Витхоффа	| 2 2 7
Диаграмма Кокстера
Группа симметрии	Д 7д , [2 + ,14], (2*7), порядок 28
Группа вращения	D 7 , [7,2] + , (722), порядок 14
Ссылки	Ю 77(е)
Двойной	Семиугольный трапецоэдр
Характеристики	выпуклый
Вершинная фигура 3.3.3.7

В геометрии семиугольная антипризма — пятая в бесконечном множестве антипризм, образованных двумя параллельными многоугольниками, разделенными полосой треугольников. В случае семиугольной антипризмы шляпки представляют собой два правильных семиугольника . В результате у этого многогранника 14 вершин и 14 граней равностороннего треугольника. Есть 14 ребер, где треугольник встречается с семиугольником, и еще 14 ребер, где встречаются два треугольника.

Семиугольная антипризма была впервые изображена Иоганном Кеплером как пример общей конструкции антипризм.