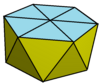
Шестиугольная антипризма

Однородная шестиугольная антипризма

Тип	Призматический однородный многогранник
Элементы	Ф = 14, Е = 24 V = 12 (х = 2)
Лица по сторонам	12{3}+2{6}
Символ Шлефли	с{2,12} ср{2,6}
Символ Витхоффа	\| 2 2 6
Диаграмма Кокстера
Группа симметрии	Д _6д , [2 ⁺,12], (2*6), порядок 24
Группа вращения	Д ₆ , [6,2] ⁺, (622), порядок 12
Ссылки	У _77(д)
Двойной	Шестиугольный трапецоэдр
Характеристики	выпуклый
Вершинная фигура 3.3.3.6

В геометрии шестиугольная антипризма является четвертой в бесконечном множестве антипризм, образованных четной последовательностью сторон треугольника, закрытых двумя вершинами многоугольников .

Антипризмы похожи на призмы, за исключением того, что основания искривлены друг относительно друга, а боковые грани представляют собой треугольники, а не четырехугольники .

В случае правильного n -стороннего основания обычно рассматривают случай, когда его копия закручена на угол $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ 180° / н ⁠$ . Дополнительная регулярность достигается за счет того, что линия, соединяющая центры оснований, перпендикулярна плоскостям основания, что делает ее прямой антипризмой . В качестве граней он имеет два $n$ -угольных основания и соединяющие эти основания $2n равнобедренных$ треугольников .

Если все грани правильные, то это полуправильный многогранник .

Скрещенная антипризма

Скрещенная шестиугольная антипризма — это звездчатый многогранник , топологически идентичный выпуклой шестиугольной антипризме с таким же расположением вершин , но его нельзя сделать однородным; стороны - равнобедренные треугольники . Конфигурация его вершин 3,3/2,3,6, с одним ретроградным треугольником. Имеет симметрию D6d _, 24-й порядок.

Связанные многогранники

Шестиугольные грани можно заменить копланарными треугольниками, что приведет к невыпуклому многограннику с 24 равносторонними треугольниками.

Однородные шестиугольные двугранные сферические многогранники
Symmetry: [6,2], (*622)							[6,2]⁺, (622)	[6,2⁺], (2*3)


{6,2}	t{6,2}	r{6,2}	t{2,6}	{2,6}	rr{6,2}	tr{6,2}	sr{6,2}	s{2,6}
Duals to uniforms

V6²	V12²	V6²	V4.4.6	V2⁶	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

Семейство однородных n -угольных антипризм
v
т
и
Название антипризмы	Дигональная антипризма	(Треугольный) Треугольная антипризма	(Тетрагональный) Квадратная антипризма	Пятиугольная антипризма	Шестиугольная антипризма	Семиугольная антипризма	...	Апейрогональная антипризма
Изображение многогранника							...
Сферическое мозаичное изображение							Плоское мозаичное изображение
Конфигурация вершины.	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	...	∞.3.3.3