сад Евклида

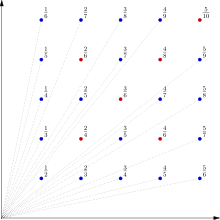
В математике , неформально говоря, сад Евклида представляет собой массив одномерных «деревьев» единичной высоты, посаженных в узлах решетки в одном квадранте квадратной решетки . ^{[ 1 ]} Более формально, сад Евклида — это набор отрезков прямых от $(x, y, 0)$ до $(x, y, 1)$ , где $x$ и $y$ — положительные целые числа .

Деревья, видимые из начала координат, — это деревья в точках решетки $(x, y, 0)$ , где $x$ и $y$ , взаимно просты т. е. где дробь $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ x / y ⁠$ находится в сокращенной форме . Название «сад Евклида» происходит от алгоритма Евклида .

Если фруктовый сад проецируется относительно начала координат на плоскость $x + y = 1$ (или, что то же самое, нарисован в перспективе с точки зрения в начале координат), вершины деревьев образуют график функции Томаэ . Точка $(x, y, 1)$ проецируется на

\left({\frac {x}{x+y}},{\frac {y}{x+y}},{\frac {1}{x+y}}\right).

Решение Базельской задачи можно использовать, чтобы показать, что доля точек в ⁠ $n\times n$ ⁠ сетка, на которой есть деревья, составляет примерно ${\tfrac {6}{\pi ^{2}}}$ и что ошибка этого приближения обращается в ноль в пределе, когда $n$ стремится к бесконечности. ^{[ 2 ]}

См. также

Проблема непрозрачного леса

Ссылки

^ Вайсштейн, Эрик В. «Сад Евклида» . Математический мир .
^ Вандервельде, Сэм (2009). «Глава 9: Скрытые сегменты». Круг в коробке . Библиотека математических кружков ИИГГ. Научно-исследовательский институт математических наук и Американское математическое общество. стр. 101–106.

Внешние ссылки

Эта статья об математики незавершена . истории Вы можете помочь Википедии, расширив ее .

[1] Вайсштейн, Эрик В. «Сад Евклида» . Математический мир .

[2] Вандервельде, Сэм (2009). «Глава 9: Скрытые сегменты». Круг в коробке . Библиотека математических кружков ИИГГ. Научно-исследовательский институт математических наук и Американское математическое общество. стр. 101–106.

[ 1 ]

[ 2 ]