Группа диэдра 6-го порядка

Граф Кэли с перестановками треугольника

График циклов с матрицами перестановок из 3 элементов
(Генераторы a и b такие же, как в графе Кэли, показанном выше.)

Таблица Кэли как таблица умножения матриц перестановок

Позиции шести элементов в таблице Кэли
Только нейтральные элементы симметричны главной диагонали, поэтому эта группа не абелева .

Таблица Кэли как общая (и специальная ) линейная группа GL(2, 2)

В математике ( D ₃ иногда обозначаемая как D ₆ ) представляет собой группу диэдра степени 3 и порядка 6. Она равна симметричной группе S ₃ . Это также наименьшая неабелева группа .

Эта страница иллюстрирует многие концепции групп на примере этой группы.

Группы симметрии

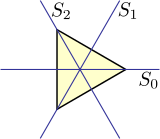
Группа диэдра D ₃ — это группа симметрии , равностороннего треугольника то есть это совокупность всех преобразований, таких как отражение, вращение и их комбинации, которые оставляют форму и положение этого треугольника фиксированными. В случае D ₃ любая возможная перестановка вершин треугольника представляет собой такое преобразование, так что группа этих симметрий изоморфна симметрической группе S ₃ всех перестановок трех различных элементов. Это не относится к диэдральным группам более высоких порядков.

Группа диэдра D ₃ изоморфна двум другим группам симметрии в трех измерениях:

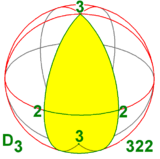
• один с осью вращения 3-го порядка и перпендикулярной осью вращения 2-го порядка (следовательно, их три): D ₃
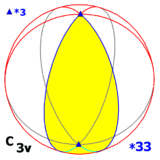
• один с осью вращения третьего порядка в плоскости отражения (а, следовательно, и в двух других плоскостях отражения): C _3v

Перестановки набора из трёх объектов

Рассмотрим три цветных блока (красный, зеленый и синий), изначально расположенные в порядке RGB. Тогда симметрическая группа S ₃ представляет собой группу всех возможных перестановок этих блоков.Если мы обозначим через a действие «поменять местами первые два блока», а через b — действие «поменять местами два последних блока», мы сможем записать все возможные перестановки в терминах этих двух действий.

В мультипликативной форме мы традиционно пишем xy для комбинированного действия «сначала сделай y , затем сделай x »; так что ab — это действие RGB ↦ RBG ↦ BRG , т. е. «взять последний блок и переместить его вперед».Если мы напишем e для «оставить блоки как они есть» (тождественное действие), то мы можем записать шесть перестановок набора из трех блоков как следующие действия:

• е : RGB ↦ RGB или ()
• а : RGB ↦ GRB или (RG)
• б : RGB ↦ RBG или (ГБ)
• ab : RGB ↦ BRG или (RGB)
• ba : RGB ↦ GBR или (RBG)
• аба : RGB ↦ BGR или (RB)

Обозначение в скобках — это обозначение цикла .

Обратите внимание, что действие aa имеет эффект RGB ↦ GRB ↦ RGB , оставляя блоки такими, какими они были; поэтому мы можем написать aa = e .Сходным образом,

• бб = е ,
• ( аба )( аба ) = е и
• ( аб ) ( ба ) знак равно ( ба ) ( аб ) знак равно е ;

поэтому каждое из вышеперечисленных действий имеет обратное.

Путем проверки мы также можем определить ассоциативность и замыкание (две необходимые групповые аксиомы ); обратите внимание, например, что

• ( ab ) a = a ( ba ) = aba , и
• ( ба ) б знак равно б ( ab ) знак равно гл .

Группа неабелева, поскольку, например, ab ≠ ba . Поскольку оно построено из основных действий a и b , мы говорим, что множество { a , b } порождает его.

В группе прошла презентация

$\langle r,a\mid r^{3}=1,a^{2}=1,ara=r^{-1}\rangle$, также написано $\langle r,a\mid r^{3},a^{2},arar\rangle$

или

$\langle a,b\mid a^{2}=b^{2}=(ab)^{3}=1\rangle$, также написано $\langle a,b\mid a^{2},b^{2},(ab)^{3}\rangle$

где a и b — обмены местами, а r = ab — циклическая перестановка. Обратите внимание, что второе представление означает, что группа является группой Кокстера . (Фактически все группы диэдра и симметрии являются группами Кокстера.)

Краткое описание групповых операций

С помощью генераторов a и b мы определяем дополнительные сокращения c := aba , d := ab и f := ba , так что a, b, c, d, e и f — все элементы этой группы. Затем мы можем суммировать групповые операции в форме таблицы Кэли :

*	и	а	б	с	д	ж
и	и	а	б	с	д	ж
а	а	и	д	ж	б	с
б	б	ж	и	д	с	а
с	с	д	ж	и	а	б
д	д	с	а	б	ж	и
ж	ж	б	с	а	и	д

Обратите внимание, что неравные неидентичные элементы коммутируют только в том случае, если они являются обратными друг другу. Следовательно, группа бесцентровая , т. е. центр группы состоит только из единичного элемента.

Классы сопряженности

Мы можем легко различить три вида перестановок трех блоков, классов сопряженности группы:

• без изменений(), элемент группы порядка 1
• меняем местами два блока: (RG), (RB), (GB), три групповых элемента порядка 2
• циклическая перестановка всех трёх блоков: (RGB), (RBG), двух групповых элементов порядка 3

Например, (RG) и (RB) имеют форму ( x y ); перестановка букв R, G и B (а именно (GB)) меняет обозначение (RG) на (RB). Следовательно, если мы применим (GB), затем (RB), а затем инверсию (GB), которая также является (GB), результирующая перестановка будет (RG).

Обратите внимание, что элементы сопряженной группы всегда имеют один и тот же порядок , но, как правило, два элемента группы, имеющие одинаковый порядок, не обязательно должны быть сопряженными.

Подгруппы

Из теоремы Лагранжа мы знаем, что любая нетривиальная подгруппа группы из 6 элементов должна иметь порядок 2 или 3. Фактически две циклические перестановки всех трех блоков с единицей образуют подгруппу порядка 3, индекса 2 и перестановки двух блоков, каждый из которых имеет единицу, образуют три подгруппы порядка 2, индекса 3. Существование подгрупп порядка 2 и 3 также является следствием теоремы Коши .

Первой из упомянутых является { (), (RGB), (RBG) }, группа чередующаяся A ₃ .

Левые 3 и правые классы A _{совпадают} (как и для любой подгруппы индекса 2) и состоят из A ₃ и множества трех перестановок { (RB), (RG), (BG) }.

Левые смежные классы { (), (RG) } :

• { (), (РГ) }
• { (РБ), (РГБ) }
• { (ГБ), (РБГ) }

Правые смежные классы { (RG), () } :

• { (РГ), () }
• { (РБГ), (РБ) }
• { (RGB), (GB) }

Таким образом, A3 _, а нормальна остальные три нетривиальные подгруппы — нет. Факторгруппа ​ G / A ₃ изоморфна C ₂ .

$G=\mathrm {A} _{3}\rtimes H$, полупрямое произведение , где H — подгруппа из двух элементов: () и одного из трёх свопов. Это разложение также является следствием (частным случаем) теоремы Шура–Цассенхауза .

С точки зрения перестановок два элемента группы G /A ₃ — это набор четных перестановок и набор нечетных перестановок.

Если исходная группа создается в результате поворота плоскости на 120° вокруг точки и отражения относительно линии, проходящей через эту точку, то факторгруппа имеет два элемента, которые можно описать как подмножества «просто повернуть ( или ничего не делай)» и «сделать зеркальное отражение ».

Обратите внимание, что для группы симметрии квадрата неравномерная перестановка вершин соответствует не зеркальному отображению, а операциям, не разрешенным для прямоугольников , т. е. повороту на 90° и применению диагональной оси отражения.

Полупрямые продукты

$\mathrm {C} _{3}\rtimes _{\varphi }\mathrm {C} _{2}$ является $\mathrm {C} _{3}\times \mathrm {C} _{2}$ если оба φ (0) и φ (1) тождественны.Полупрямое произведение изоморфно группе диэдра порядка 6, если φ (0) — тождество, а φ (1) — нетривиальный автоморфизм C ₃ , инвертирующий элементы.

Таким образом мы получаем:

( п ₁ , 0) * ( п ₂ , час ₂ ) знак равно ( п ₁ + п ₂ , час ₂ )

( п ₁ , 1) * ( п ₂ , час ₂ ) знак равно ( п ₁ - п ₂ , 1 + час ₂ )

для всех n ₁ , n ₂ в C ₃ и h ₂ в C ₂ .Более кратко,

$(n_{1},h_{1})*(n_{2},h_{2})=(n_{1}+(-1)^{h_{1}}n_{2},h_{1}+h_{2})$

для всех n ₁ , n ₂ в C ₃ и h ₁ , h ₂ в C ₂ .

В таблице Кэли:

	00	10	20	01	11	21
00	00	10	20	01	11	21
10	10	20	00	11	21	01
20	20	00	10	21	01	11
01	01	21	11	00	20	10
11	11	01	21	10	00	20
21	21	11	01	20	10	00

Обратите внимание, что для второй цифры у нас по сути есть таблица 2×2 с равными значениями 3×3 для каждой из этих 4 ячеек. Для первой цифры левая половина таблицы такая же, как и правая, но верхняя половина отличается от нижней.

Для прямого произведения таблица такая же, за исключением того, что первые цифры нижней половины таблицы такие же, как и в верхней половине.

Групповое действие

Рассмотрим D ₃ геометрически, как группу симметрии изометрий групповое плоскости, и рассмотрим соответствующее действие на набор из 30 равномерно расположенных точек окружности с номерами от 0 до 29, с 0 на одной из осей отражения.

В этом разделе иллюстрируются концепции групповых действий для этого случая.

Действие G на X называется

• транзитивно , если для любых двух x , y в X существует g в G такой, что g · x = y ; это не тот случай
• верный (или эффективный ), если для любых двух различных g , h в G существует x в X такой, что g · x ≠ h · x ; это так, потому что, кроме тождества, группы симметрии не содержат элементов, которые «ничего не делают».
• свободен , если для любых двух различных g , h в G и всех x в X имеем g · x ≠ h · x ; это не так, потому что есть отражения

Орбиты и стабилизаторы

Орбиты 30 равномерно расположенных точек на окружности под групповым действием D ₃

Орбита может быть точки x в X — это набор элементов X, который x перемещен элементами G. в Орбита x обозначается Gx :

$Gx=\left\{g\cdot x\mid g\in G\right\}$

Орбиты: {0, 10, 20}, {1, 9, 11, 19, 21, 29}, {2, 8, 12, 18, 22, 28}, {3, 7, 13, 17, 23, 27}, {4, 6, 14, 16, 24, 26} и {5, 15, 25}. Точки внутри орбиты «эквивалентны». Если для узора применяется группа симметрии, то внутри каждой орбиты цвет один и тот же.

Множество всех орбит X под действием G записывается как X / G .

Если Y является подмножеством X GY , мы пишем и множества { g · y : y ∈ Y g для ∈ G }. Мы называем подмножество Y инвариантным относительно G , если GY = Y (что эквивалентно GY ⊆ Y ) . В этом случае G действует на Y. также Подмножество Y называется фиксированным относительно G, если g · y = y для всех g в G и всех y в Y . Объединение, например, двух орбит инвариантно относительно G , но не фиксировано.

Для каждого x в X мы определяем стабилизатора подгруппу x (также называемую группой изотропии или маленькой группой ) как набор всех элементов в G , которые фиксируют x :

$G_{x}=\{g\in G\mid g\cdot x=x\}$

Если x — точка отражения (0, 5, 10, 15, 20 или 25) , ее стабилизатором является группа второго порядка, содержащая единицу и отражение в x . В остальных случаях стабилизатором является тривиальная группа.

Для фиксированного x в X рассмотрим отображение G в X, заданное формулой g ↦ g · x . Образ этой карты — это орбита x , а кообраз — это набор всех левых классов смежных G _x . Тогда стандартная теорема о факторах теории множеств дает естественную биекцию между G / G _x и Gx . В частности, биекция задается формулой hG _x ↦ h · x . Этот результат известен как теорема о стабилизаторе орбиты . В двух случаях малой орбиты стабилизатор нетривиален.

Если два элемента и y принадлежат одной и той же орбите, то их стабилизирующие подгруппы G _x и G _y изоморфны x . Точнее: если y = g · x , то G _y = gG _x g ⁻¹ . В примере это применимо, например, для 5 и 25, обеих точек отражения. Отражение около 25 соответствует вращению 10, отражение около 5 и вращению -10.

Результатом, тесно связанным с теоремой о стабилизаторе орбиты, является лемма Бернсайда :

$\left|X/G\right|={\frac {1}{\left|G\right|}}\sum _{g\in G}\left|X^{g}\right|$

где Х ^г - это набор точек, фиксированных g . Т.е. количество орбит равно среднему числу точек, закрепленных на элементе группы.

Для идентичности все 30 точек фиксированы, для двух вращений — ни одной, а для трех отражений — по две: {0, 15}, {5, 20} и {10, 25}. Таким образом, среднее число витков равно шести.

Теория представлений

С точностью до изоморфизма эта группа имеет три неприводимых комплексных унитарных представления, которые мы назовем $I$ (тривиальное представление), $\rho _{1}$ и $\rho _{2}$, где нижний индекс указывает размерность. По своему определению как группа перестановок над множеством из трех элементов, группа имеет представление на $\mathbb {C} ^{3}$ путем перестановки элементов вектора, фундаментального представления. Это представление не является неприводимым, поскольку оно распадается в прямую сумму $I$ и $\rho _{2}$. $I$ появляется как подпространство векторов формы $(\lambda ,\lambda ,\lambda ),\lambda \in \mathbb {C}$ и $\rho _{2}$ - это представление в его ортогональном дополнении, которое представляет собой векторы вида $(\lambda _{1},\lambda _{2},-\lambda _{1}-\lambda _{2})$.Нетривиальное одномерное представление $\rho _{1}$ возникает через группы $\mathbb {Z} _{2}$ градация: действие – умножение на знак перестановки элемента группы. Любая конечная группа имеет такое представление, поскольку по своему регулярному действию она является подгруппой циклической группы. Подсчет квадратных размеров изображений ( $1^{2}+1^{2}+2^{2}=6$, порядок группы), мы видим, что это должны быть все неприводимые представления.

Двумерное неприводимое линейное представление дает одномерное проективное представление (т. е. действие на проективной прямой , вложение в группу Мёбиуса PGL(2, C ) ), как эллиптические преобразования . Это может быть представлено матрицами с элементами 0 и ±1 (здесь они записаны как дробные линейные преобразования ), известными как ангармоническая группа :

• заказ 1: $z$
• заказ 2: $1-z,1/z,z/(z-1)$
• заказ 3: $(z-1)/z,1/(1-z)$

и, таким образом, сводится к представлению над любым полем, которое всегда является точным/инъективным (поскольку никакие два термина не отличаются только знаком). Над полем из двух элементов проективная прямая имеет только 3 точки, и, таким образом, это исключительный изоморфизм $S_{3}\approx \mathrm {PGL} (2,2).$ В характеристике 3 это вложение стабилизирует точку $-1=[-1:1],$ с $2=1/2=-1$ (в характеристике больше 3 эти точки различны и переставлены местами и являются орбитой гармонического двойного отношения ). Над полем с тремя элементами проективная прямая имеет 4 элемента, и поскольку PGL(2, 3) изоморфна симметрической группе из 4 элементов S ₄ , полученное вложение $\mathrm {S} _{3}\hookrightarrow \mathrm {S} _{4}$ равен стабилизатору точки $-1$.

См. также

• Группа диэдра 8-го порядка

Ссылки

• Фрэли, Джон Б. (1993), Первый курс абстрактной алгебры (5-е изд.), Аддисон-Уэсли, стр. 93–94, ISBN  978-0-201-53467-2

Внешние ссылки

• http://mathworld.wolfram.com/DihedralGroupD3.html
• https://groupprops.subwiki.org/wiki/Symmetric_group:S3