Металлическое средство

Соотношения золота, серебра и бронзы внутри соответствующих прямоугольников.

Металлическое среднее (также металлическое соотношение , металлическая константа или благородное среднее). ) натурального числа n — положительное действительное число , обозначаемое здесь $S_{n},$ который удовлетворяет следующим эквивалентным характеристикам:

• уникальное положительное действительное число $x$ такой, что ${\textstyle x=n+{\frac {1}{x}}}$
• положительный корень квадратного уравнения $x^{2}-nx-1=0$
• число ${\textstyle {\frac {n+{\sqrt {n^{2}+4}}}{2}}}$
• число, выражение которого в виде цепной дроби есть

  $[n;n,n,n,n,\dots ]=n+{\cfrac {1}{n+{\cfrac {1}{n+{\cfrac {1}{n+{\cfrac {1}{n+\ddots \,}}}}}}}}$

Металлические средства являются обобщением золотого сечения ( $n=1$) и соотношение серебра ( $n=2$), и поделиться некоторыми из их интересных свойств. Термин «бронзовое соотношение» ( $n=3$), а термины, использующие названия других металлов (например, медь или никель), иногда используются для обозначения последующих металлических средств.

С точки зрения теории алгебраических чисел металлические средние — это в точности действительные квадратичные целые числа , большие $1$ и иметь $-1$ как их норма .

Определяющее уравнение $x^{2}-nx-1=0$ го n- металлического среднего представляет собой характеристическое уравнение линейного рекуррентного соотношения вида $x_{k}=nx_{k-1}+x_{k-2}.$ Отсюда следует, что с учетом такой повторяемости решение можно выразить как

$x_{k}=aS_{n}^{k}+b\left({\frac {-1}{S_{n}}}\right)^{k},$

где $S_{n}$ — n -е металлическое среднее, а a и b — константы, зависящие только от $x_{0}$ и $x_{1}.$ Поскольку обратное металлическое среднее меньше 1 , эта формула подразумевает, что частное двух последовательных элементов такой последовательности стремится к металлическому среднему, когда k стремится к бесконечности.

Например, если $n=1,$ $S_{n}$ это золотое сечение . Если $x_{0}=0$ и $x_{1}=1,$ последовательность является последовательностью Фибоначчи , а приведенная выше формула является формулой Бине . Если $n=1,x_{0}=2,x_{1}=1$ у одного есть числа Лукаса . Если $n=2,$ металлическое среднее называется отношением серебра , а элементы последовательности, начинающиеся с $x_{0}=0$ и $x_{1}=1$ называются числами Пелла . Третье металлическое среднее иногда называют «бронзовым соотношением».

Геометрия

Если удалить n наибольших возможных квадратов из прямоугольника с соотношением длины и ширины, равным n-му металлическому среднему, получится прямоугольник с таким же соотношением длины и ширины (на рисунках n — количество пунктирных линий).

Золотое сечение в пентаграмме ( φ = красный/зеленый = зеленый/синий = синий/фиолетовый) и сечение серебра в восьмиугольнике.

Определяющее уравнение ${\textstyle x=n+{\frac {1}{x}}}$ го n- металлического среднего приводит к следующей геометрической интерпретации.

Рассмотрим прямоугольник , отношение его длины L к ширине W есть n- е металлическое отношение. Если из этого прямоугольника удалить n квадратов со стороной W , то получится прямоугольник, аналогичный исходному; то есть прямоугольник с одинаковым соотношением длины к ширине (см. рисунки).

- е n металлическое отношение — это среднее арифметическое и гипотенузы кратчайшего катета прямоугольного треугольника с длинами сторон 2 и n . Это следует из значения ${\frac {n+{\sqrt {n^{2}+4}}}{2}}$ и теорема Пифагора .

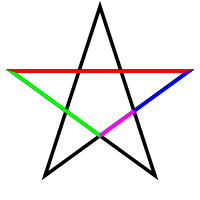
Некоторые металлические средства выглядят как сегменты фигуры, образованной правильным многоугольником и его диагоналями. Это, в частности, относится к золотому сечению и пятиугольнику , а также к серебряному сечению и восьмиугольнику ; см. цифры.

Полномочия

Обозначая $S_{m}$ металлическое среднее m у каждого есть

$S_{m}^{n}=K_{n}S_{m}+K_{n-1},$

где цифры $K_{n}$ определяются рекурсивно начальными условиями K ₀ = 0 и K ₁ = 1 ,и рекуррентное соотношение

$K_{n}=mK_{n-1}+K_{n-2}.$

Доказательство. Равенство немедленно справедливо для $n=1.$ Рекуррентное соотношение подразумевает $K_{2}=m,$ что делает равенство верным для $k=2.$ Предположим, что равенство верно с точностью до $n-1,$ у одного есть

${\begin{aligned}S_{m}^{n}&=mS_{m}^{n-1}+S_{m}^{n-2}&&{\text{(defining equation)}}\\&=m(K_{n-1}S_{n}+K_{n-2})+(K_{n-2}S_{m}+K_{n-3})&&{\text{(recurrence hypothesis)}}\\&=(mK_{n-1}+K_{n-2})S_{n}+(mK_{n-2}+K_{n-3})&&{\text{(regrouping)}}\\&=K_{n}S_{m}+K_{n-1}&&{\text{(recurrence on }}K_{n}).\end{aligned}}$

Конец доказательства.

У одного также есть

$K_{n}={\frac {S_{m}^{n+1}-(m-S_{m})^{n+1}}{\sqrt {m^{2}+4}}}.$

Нечетные силы металлического средства сами по себе являются металлическими средствами. Точнее, если n — нечетное натуральное число, то $S_{m}^{n}=S_{M_{n}},$ где $M_{n}$ определяется рекуррентным соотношением $M_{n}=mM_{n-1}+M_{n-2}$ и начальные условия $M_{0}=2$ и $M_{1}=m.$

Доказательство: Пусть $a=S_{m}$ и $b=-1/S_{m}.$ Определение металлических средств подразумевает, что $a+b=m$ и $ab=-1.$ Позволять $M_{n}=a^{n}+b^{n}.$ С $a^{n}b^{n}=(ab)^{n}=-1$ если n нечетно, то степень $a^{n}$ является корнем $x^{2}-M_{n}-1=0.$ Итак, осталось доказать, что $M_{n}$ — целое число, удовлетворяющее заданному рекуррентному соотношению. Это следует из тождества

${\begin{aligned}a^{n}+b^{n}&=(a+b)(a^{n-1}+b^{n-1})-ab(a^{n-2}+a^{n-2})\\&=m(a^{n-1}+b^{n-1})+(a^{n-2}+a^{n-2}).\end{aligned}}$

На этом доказательство закончено, поскольку исходные значения легко проверить.

В частности, имеется

${\begin{aligned}S_{m}^{3}&=S_{m^{3}+3m}\\S_{m}^{5}&=S_{m^{5}+5m^{3}+5m}\\S_{m}^{7}&=S_{m^{7}+7m^{5}+14m^{3}+7m}\\S_{m}^{9}&=S_{m^{9}+9m^{7}+27m^{5}+30m^{3}+9m}\\S_{m}^{11}&=S_{m^{11}+11m^{9}+44m^{7}+77m^{5}+55m^{3}+11m}\end{aligned}}$

и вообще,

$S_{m}^{2n+1}=S_{M},$

где

$M=\sum _{k=0}^{n}{{2n+1} \over {2k+1}}{{n+k} \choose {2k}}m^{2k+1}.$

С четными степенями дела обстоят сложнее. Если n — положительное четное целое число, то

${S_{m}^{n}-\left\lfloor S_{m}^{n}\right\rfloor }=1-S_{m}^{-n}.$

Кроме того,

${1 \over {S_{m}^{4}-\left\lfloor S_{m}^{4}\right\rfloor }}+\left\lfloor S_{m}^{4}-1\right\rfloor =S_{\left(m^{4}+4m^{2}+1\right)}$

${1 \over {S_{m}^{6}-\left\lfloor S_{m}^{6}\right\rfloor }}+\left\lfloor S_{m}^{6}-1\right\rfloor =S_{\left(m^{6}+6m^{4}+9m^{2}+1\right)}.$

Обобщение

Можно определить металлическое среднее $S_{-n}$ отрицательного целого числа − n как положительное решение уравнения $x^{2}-(-n)-1.$ Металлическое среднее - n является мультипликативным обратным металлическому среднему n :

$S_{-n}={\frac {1}{S_{n}}}.$

Другое обобщение состоит в изменении определяющего уравнения с $x^{2}-nx-1=0$ к $x^{2}-nx-c=0$. Если

$R={\frac {n\pm {\sqrt {n^{2}+4c}}}{2}},$

любой корень уравнения, то есть

$R-n={\frac {c}{R}}.$

Серебряное среднее m также определяется интегралом

$S_{m}=\int _{0}^{m}{\left({x \over {2{\sqrt {x^{2}+4}}}}+{{m+2} \over {2m}}\right)}\,dx.$

Другая форма металлического среднего —

${\frac {n+{\sqrt {n^{2}+4}}}{2}}=e^{\operatorname {arsinh(n/2)} }.$

Числовые значения

Первые металлические средства
Н	Соотношение	Ценить	Имя
0	0 + √ 4 / 2	1
1	1 + √ 5 / 2	1.618033989	Золотой
2	2 + √ 8 / 2	2.414213562	Серебро
3	3 + √ 13 / 2	3.302775638	Бронза
4	4 + √ 20 / 2	4.236067978
5	5 + √ 29 / 2	5.192582404
6	6 + √ 40 / 2	6.162277660
7	7 + √ 53 / 2	7.140054945
8	8 + √ 68 / 2	8.123105626
9	9 + √ 85 / 2	9.109772229
10	10+ √ 104 / 2	10.099019513

См. также

• Постоянный
• Иметь в виду
• Соотношение
• Пластиковое соотношение

Дальнейшее чтение

• Стахов, Алексей Петрович (2009). Математика гармонии: от Евклида к современной математике и информатике , с. 228, 231. World Scientific. ISBN   9789812775832 .

Внешние ссылки

• Кристина-Елена Грецкану и Мирча Красмаряну (2013). « Металлические структуры на римановых многообразиях », журнал Аргентинского математического союза .
• Ракочевич, Милое М. « Дальнейшее обобщение золотой середины по отношению к «божественному» уравнению Эйлера », Arxiv.org .